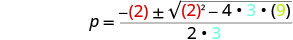
A quadratic can be negative for some or all of the x values in its domain. This will depend on the coefficients, but a quadratic with three negative coefficients is not necessarily always negative. Remember that a quadratic function has the form: f (x) = ax2 + bx + c where a, b, and c are real numbers and a is nonzero.
How to prove a quadratic equation is always positive?
- The roots of quadratic equation are equal in magnitude but of opposite sign if b = 0 and ac < 0
- The root with greater magnitude is negative if the sign of a = sign of b × sign of c
- If a > 0, c < 0 or a > 0, c > 0; the roots of quadratic equation will have opposite sign
- If y = ax2+ bx + c is positive for all real values of x, a > 0 and D < 0
What are the steps for solving a quadratic equation?
What are the 7 steps in solving quadratic equation by completing the square?
- Isolate the number or variable c to the right side of the equation.
- Divide all terms by a (the coefficient of x2, unless x2 has no coefficient).
- Divide coefficient b by two and then square it.
- Add this value to both sides of the equation.
How do you write a quadratic equation?
Writing Quadratic Equations
- Plug in the coordinates for x and y into the general form. Remember y and f (x) represent the same quantity.
- Simplify. (Remember the order of operations)
- Repeat steps 1 & 2 for the other two points.
- Take two equations at a time and eliminate one variable (c works well)
- Then repeat using two equations and eliminate the same variable you eliminated in #4.
Unit/writingquads.html More items...
Can a quadratic equation have only one real solution?
The first way to tell if a quadratic has one solution is to look at the discriminant. If the discriminant is zero, then the quadratic equation has only one real solution. The discriminant is the expression b2 – 4ac under the radical in the quadratic formula. Its sign can tell us the nature of the solutions of the corresponding quadratic equation.
What if A is negative in a quadratic formula?
0:105:08Negative Underneath Root in Quadratic Formula (Imaginary ...YouTubeStart of suggested clipEnd of suggested clipSo negative negative B is 4 plus or minus square root negative 4 squared minus 4 is 1 C is 9 allMoreSo negative negative B is 4 plus or minus square root negative 4 squared minus 4 is 1 C is 9 all divided by 2. And then so when we work that out we get 4 plus or minus square.
Can standard form have a negative A?
Summary of Standard Form Rules for Linear Equations: A, B, and C must be integers (not fractions) A can not be negative. A, B, and C should have no common factors other than 1.
Is a positive in standard form?
Standard form is just another way to write a linear equation equation along with slope intercept form and point slope form. The constants, A, B, and C, must be integers. And A must be positive. An example of a line in standard form would be: 4x+7y=12 Here, 4, 7, and 12 are all whole numbers, and 4 is positive.
Can a be negative in standard form of parabola?
Vertex Form Equation for Parabola Just like the standard form, the first number, a, tells you whether the parabola opens up or down. If it's positive, it opens up and if it's negative, it opens down.
What are the rules for standard form?
The Standard Form for a linear equation in two variables, x and y, is usually given as Ax + By = C where, if at all possible, A, B, and C are integers, and A is non-negative, and, A, B, and C have no common factors other than 1.
How do you put a negative exponent in standard form?
1:224:06standard form - negative powers - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo we want to have one two three four. So really 0.0003 4 is the same as saying 3.4 times 10 to theMoreSo we want to have one two three four. So really 0.0003 4 is the same as saying 3.4 times 10 to the minus 4. So the basic idea is that you always have to have one number here followed by a comma.
What does a negative power mean in standard form?
10 − 5 = 0.00001. 10 − 6 = 0.000001. Notice that a negative power does not mean that the number is negative. It means that we have gone from multiplying by 10 to dividing by 10.
What does standard form look like?
The standard form for linear equations in two variables is Ax+By=C. For example, 2x+3y=5 is a linear equation in standard form. When an equation is given in this form, it's pretty easy to find both intercepts (x and y). This form is also very useful when solving systems of two linear equations.
How to solve -3x2+10x3=0?
Sal solves -3x^2+10x-3=0 by plugging a=-3, b=10, c=-3 in the quadratic formula. Then he multiplies everything by -1 and solves again. The results are the same! Created by Sal Khan and Monterey Institute for Technology and Education.
Can you use quadratic formulas on any equation?
So, the quadratic formula can be used on ANY quadratic equation, but isolating the square, the zero-product property, and completing the square cannot. So, is it efficient just to use the quadratic formula every time?
Does quadratic formula work for all quadratics?
Yes, it works for all quadratic equations. You just need to simplify the quadratic and write it in the form: Ax^2 + Bx + C = 0 before using the formula. Comment on Kim Seidel's post “Yes, it works for all qua...”. Button opens signup modal.
What would happen if the negative wasn't there?
We can see that if the negative weren't there, this would be a quadratic with a leading coefficient of {eq}1 {/eq} and we might attempt to factor by the sum-product method . Luckily, we can re-write this equation by factoring the negative sign out to the front. Doing this flips the sign of each term, and we get:
What happens when you multiply negative back in?
Notice that we haven't changed the value of the equation - if we multiply the negative back in, we get back our original equation. Now we're able to focus on simply factoring the equation that is inside the brackets, and the negative sign comes along for the ride.
Can a quadratic equation be factored?
Remember that not every quadratic equation can be factored, regardless of whether it has a negative leading coeffi cient or not. If the above methods don't work, we can always use the quadratic formula to find factors of a quadratic (provided they exist).
Can you factor a negative coefficient?
Suppose we have a quadratic equation that has a negative coefficient in front of it, and we'd like to factor. This is no problem - we can actually factor the negative out to the front of the equation, and then work on factoring as normal. Let's go through a few different examples here.
What does it mean when the solution of a quadratic equation is negative?
It means that the solution (s) to the quadratic equation is negative. There isn’t anything wrong with having a negative answer.
What happens if b2-4ac in the quadratic equation gives a negative answer?
What happens if b²-4ac in the quadratic equation gives a negative answer? That would mean that the quadratic has no real solution
How to find if a function is positive or negative?
Solve by factoring, completing the square, or using the quadratic formula. If the function crosses the x axis twice at, say x=m and x=n, then check to see if it opens up or down. If it opens up, then it is negative between m and n, and positive elsewhere (except where it is 0). If it opens down, then it is positive between m and n, and negative elsewhere. If there is only one solution, and the function opens up, then it is positive everywhere except where it is equal to 0. If it opens down, then it is negative everywhere except where it equals 0. If there are no real solutions, then it is either always positive (if it opens up) or always negative (if it opens down).
What is the formula for quadratic?
The quadratic formula consists of coefficients of x^2 ,x and the constant term.
Does a quadratic have a real number solution?
If ( b²-4ac ) < 0, then not only does the quadratic have no REAL NUMBER solution, but it does have a COMPLEX NUMBER solution (s).
Can x be negative?
As far as i know about quadratic equations there is no convention like “ x cannot be negative” .
Is a solution a real number?
In this case while a solution may not exist as a Real Number, (that is it may not exist on the Number Line) it does exist as a Complex Number.
