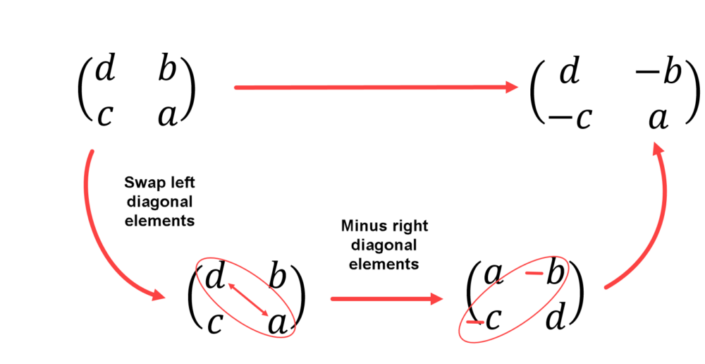
What is the determinant of a matrix having one row?
Determinant of a Matrix having one row (column) multiple of another row (column) is equal to 0. If, we have any matrix in which one of the row (or column) is multiple of another row (or column) then determinant of such a matrix is equal to zero.
How do you find the determinant of a 4×4 matrix?
For 4×4 Matrices and Higher. The pattern continues for 4×4 matrices: plus a times the determinant of the matrix that is not in a's row or column, minus b times the determinant of the matrix that is not in b's row or column, plus c times the determinant of the matrix that is not in c's row or column,
What is the determinant of a 3x6 matrix?
A Matrix is an array of numbers: A Matrix. (This one has 2 Rows and 2 Columns) The determinant of that matrix is (calculations are explained later): 3×6 − 8×4 = 18 − 32 = −14.
How hard is it to memorize the determinant of a matrix?
We denote this as Okay, that was a lot of work for a simple fact. Most students don't have any trouble memorizing the determinant of a 2 × 2 matrix without such rigmarole. The reason for going through this process was to make calculating a 3 × 3 (and larger) determinant easy. in the exact same way.

Can there be more than one determinant?
Thus, the value of the determinant of of every matrix is determined by the definition. There can be only one determinant function.
Does a matrix only have one determinant?
The determinant is only defined for square matrices (M x M). A matrix has exactly one determinant, since it is a scalar, containing information about the matrix. The determinant equals zero for singular matrices.
Can matrices have different determinants?
Hence, we cay say that, two matrices of different values can have the same value of determinant.
What are the rules of determinants?
There are 10 main properties of determinants: reflection property, all-zero property, proportionality or repetition property, switching property, scalar multiple properties, sum property, invariance property, factor property, triangle property, and co-factor matrix property.
What if the determinant is zero?
When the determinant of a matrix is zero, the volume of the region with sides given by its columns or rows is zero, which means the matrix considered as a transformation takes the basis vectors into vectors that are linearly dependent and define 0 volume.
Is determinant only for square matrix?
The determinant only exists for square matrices (2×2, 3×3, ... n×n). The determinant of a 1×1 matrix is that single value in the determinant. The inverse of a matrix will exist only if the determinant is not zero.
What is true regarding determinant of matrix?
Explanation: The concept of determinant is applicable to square matrices only is true regarding Determinant of a Matrix.
What if the determinant is 1?
Determinants are defined only for square matrices. If the determinant of a matrix is 0, the matrix is said to be singular, and if the determinant is 1, the matrix is said to be unimodular.
What if two determinants are equal?
If two rows (or columns) of a determinant are identical the value of the determinant is zero. Hence, option (1) is correct.
What is the difference between matrix and determinant?
What is the determinant of the matrix [36−12]?...MatrixDeterminantA matrix is an arrangement of numbers in rows and columns to form an array.A determinant is a scalar value that is calculated from a matrix.2 more rows
Why is the determinant of a singular matrix 0?
The determinant of a singular matrix is zero Since a matrix is either invertible or singular, the two logical implications ("if and only if") follow.
How do you verify a determinant?
If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then the value of the determinant is zero. Proof: If we interchange the identical rows (or columns) of the determinant Δ, then Δ does not change.
What does it mean for a matrix to have one determinant?
Determinants are defined only for square matrices. If the determinant of a matrix is 0, the matrix is said to be singular, and if the determinant is 1, the matrix is said to be unimodular.
What is determinant in a matrix?
The determinant of a matrix is the scalar value computed for a given square matrix. Linear algebra deals with the determinant, it is computed using the elements of a square matrix. It can be considered as the scaling factor for the transformation of a matrix.
What is the determinant of a single row matrix?
Determinant of a matrix A is denoted by |A| or det(A). Properties of Determinants of Matrices: Determinant evaluated across any row or column is same. If all the elements of a row (or column) are zeros, then the value of the determinant is zero.
What is the determinant of a matrix from one element?
A 1 × 1 matrix is a row with only one row and one column, and hence only one element. The determinant of every 1 × 1 matrix is always equal to the matrix element. Example: If matrix A = [69]1 × 1, then det A or |A| = 69. then its determinant is given by ad – bc.
Calculating The Determinant
First of all the matrix must be square (i.e. have the same number of rows as columns). Then it is just basic arithmetic. Here is how:
For A 2×2 Matrix
For a 2×2 matrix (2 rows and 2 columns):The determinant is:|A| = ad − bc "The determinant of A equals a times d minus b times c"
For A 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):The determinant is:|A| = a(ei − fh) − b(di − fg) + c(dh − eg) "The determinant of A equals ... etc"It may l...
For 4×4 Matrices and Higher
The pattern continues for 4×4 matrices: 1. plus a times the determinant of the matrix that is not in a's row or column, 2. minus b times the determ...
What is the purpose of the matrix determinant?
Determinant is used to know whether the matrix can be inverted or not, it is useful in analysis and solution of simultaneous linear equations (Cramer’s rule), used in calculus, used to find area of triangles (if coordinates are given) and more. Determinant of a matrix A is denoted by |A| or det (A).
How many determinants are there in a determinant?
In a determinant each element in any row (or column) consists of the sum of two terms, then the determinant can be expressed as sum of two determinants of same order. For example,
What happens when two rows of a determinant are interchanged?
If any two row (or two column) of a determinant are interchanged the value of the determinant is multiplied by -1.
What is the value of a determinant if two rows are identical?
If two rows (or columns) of a determinant are identical the value of the determinant is zero.
Is the determinant evaluated across any row or column?
Determinant evaluated across any row or column is same.
What is the determinant of a matrix?
Determinant is a scalar value that can be calculated from the elements of a square matrix. It is an arrangement of numbers in the form#N#∣ a b c d ∣#N#left| begin {matrix} a & b \ c & d \ end {matrix} right| ∣∣∣∣∣#N##N#a c#N##N#b d#N##N#∣∣∣∣∣#N##N#. Determinant for a 3×3 matrix is determined by#N#∣ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ∣#N#begin {vmatrix} a_ {1} & b_ {1} & c_ {1}\ a_ {2}& b_ {2} & c_ {2}\ a_ {3}& b_ {3} & c_ {3} end {vmatrix} ∣∣∣∣∣∣∣#N##N#a1#N##N#a2#N##N#a3#N# #N#b1#N##N#b2#N##N#b3#N# #N#c1#N##N#c2#N##N#c3#N# #N#∣∣∣∣∣∣∣#N##N#= a1(b2c3-b3c2)-b1(a2c3-a3c2)+c1(a2b3-a3b2). In this article, we come across properties of determinants, multiplication of determinants and determinants formula.
What happens to the determinant if the columns and rows are interchanged?
Suppose any two rows or columns of a determinant are interchanged, then its sign changes. If any two rows or columns of a determinant are the same, then the determinant is 0.
What is the shape of a determinant?
In a determinant, horizontal lines are known as rows and vertical lines are known as columns. The shape of every determinant is a square. If a determinant is of order n then it contains n rows and n columns. E.g.
What is the determinant of a matrix?
The determinant of a matrix. A matrix is an array of many numbers. For a square matrix, i.e., a matrix with the same number of rows and columns, one can capture important information about the matrix in a just single number, called the determinant. The determinant is useful for solving linear equations, capturing how linear transformation change ...
Do we need absolute value of determinant?
Side note: Sometimes, we'll need the absolute value of a determinant. How can we denote this? We don't want to put another pair of vertical lines around the determinant when using this notation. (If we did, we'd end up with double vertical lines, which could be confused with something called the “norm” of a matrix—you'll learn about matrix norms in linear algebra.) So instead, when we have to write the absolute value of a determinant, we'll use the original notation, for example,
Do vertical lines mean absolute value?
However, note that in this case, the vertical lines do not mean absolute value. The determinant can be negative. In mathematics, we like to use the same symbols to mean different things, which is okay as long as it's clear from context. Since the absolute value of an array of numbers is meaningless, the notation is unambiguous.
Can you memorize a determinant of a 2 x 2 matrix?
Okay, that was a lot of work for a simple fact. Most students don't have any trouble memorizing the determinant of a 2 × 2 matrix without such rigmarole. The reason for going through this process was to make calculating a 3 × 3 (and larger) determinant easy.
What is the determinant of a matrix with a single column?
With only a very slightly greater amount of work, you can see that a matrix with a single column or a single row of all zero entries will have a zero determinant. Moving into slightly more non-obvious territory, if one column is a fixed scalar multiple of another column, or one row is a fixed scalar multiple of another row, then the determinant is zero .
What is the determinant value of a matrix that does not have all rows?
a. A matrix which does not have all rows (or Column) linearly independent will have a Determinant value of 0.
What is the determinant of a parallelogram?
The determinant then is a measure of the area (2D), volume (3D), hypervolume (4D++) of the parallelogram (2D), parallelepiped (3D), or hyperparallelepiped (4D++) defined by the columns of the matrix. For an illustrated proof of the 2D case where det ( [a b;c d]) = ad-bc, see Geometry of Determinant, but the basic idea is quite general.
What is the other term for a matrix that is not invertible?
The other term for a matrix that’s not invertible is “singular matrix”. As to why it’s called that, see the question Why is a matrix whose determinant is 0 called a singular matrix?
What is matrix transform?
Whether or not you're actually using it in a geometrical context, a matrix can be interpreted as a geometrical transform that applies to vectors, or shapes built from vectors. It's most common to define the transform by left-multiplying the matrix into a column vector, as in Ax=b, or a batch of column vectors grouped into a matrix, as in AX=B. Then any particular matrix can be interpreted as a combination of sc
What does it mean when a determinant is negative?
If the determinant is negative, it means the A flips the orientation. If it's 1, it means the matrix preserves area/volume/hypervolume. If it's 0, it means it squashes shapes flat in at least one dimension.
What is the determinant of identity matrix?
So the determinant of an identity matrix is the area/volume/hypervolume of a unit square/cube/hypercube, i.e., 1. And det (A) is both the volume of the shape defined by the columns of A and the factor by which the area/volume/hypervolume of any shape is changed when you transform it by A.