How to find the common factors of a polynomial?
example
- Find the GCF of all the terms of the polynomial. Find the GCF of 2x 2 x and 14 14.
- Rewrite each term as a product using the GCF. Rewrite 2x 2 x and 14 14 as products of their GCF, 2 2.
- Use the Distributive Property ‘in reverse’ to factor the expression.
- Check by multiplying the factors. Box 1: Enter your answer as an expression. ...
How do you find the derivative of a polynomial?
Polynomials are one of the simplest functions to differentiate. When taking derivatives of polynomials, we primarily make use of the power rule. Power Rule. For a real number. n. n n, the derivative of. f ( x) = x n. f (x)= x^n f (x) = xn is. d d x f ( x) = n x n − 1.
What counts as a polynomial?
A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using the mathematical operations such as addition, subtraction, multiplication and division (No division operation by a variable).
Can a coefficient have an exponent?
a + b is Variables only. In this case the variable appears to have no exponent, then it has an exponent of 1: x1 = x 8m = 8 is the coefficient, and m is the base, so 1 will be the exponent. (8m 1) Like Terms: if it has the same base and same exponents (2a 2 and -6a 2)

What is a polynomial?
Polynomial is a number of terms in one or more variables ( mostly denoted by the lower case letters x, y, t, etc). The terms of the expression are separated from each other by + or - signs. The variables have coefficients generally denoted by lower case letters a, b, c etc. The powers of the variables are 0, 1, 2,3,4, ……., i.e. whole numbers. The powers need to be whole numbers as it is the requirement by definition of a polynomial.
When you divide a polynomial by the denominator, does the polynomial return?
Because in such a case, the polynomial in the numerator will return a polynomial with degree of at least ‘1’ when you divide it by the denominator.
What is improper fraction?
By analogy, the polynomial fraction R ( x) P ( x) is called improper if the numeraotor contains P ( x) at least once PLUS a polynomial with degree less than that of the denominator. So you write it as R ( x) P ( x) = Q ( x) + M ( x) P ( x)
What is a polynomial in one variable?
A polynomial in one variable is a function in which the variable is only to whole number powers, and the variable does not appear in denominators, in exponents, under radicals, or in between absolute value signs or greatest integer signs.
Why are polynomials defined as they are?
The reason why polynomials are defined as they are is because they have a whole bunch of really neat properties. For example, if you substitute a polynomial into another polynomial, you always get another polynomial. If we try that with the newly named extended polynomial: f (x) = x^ (1/2) g (x) = 1 - x^2.
What is the degree of P (x) = 6x?
P (x) = 6x is a polynomial of degree 1.
Can you reason about a polynomial?
It can, it’s just that it won’t be a polynomial (in general), and you won’t be able to reason about it using most of the tools that polynomials provide.
What are some examples of exponents?
Exponents - exponents are usually attached to variables but can also be found with a constant. Examples of exponents include the 2 in 5² or the 3 in x³.
What happens when you multiply polynomials?
Polynomials often represent a function. And if you graph a polynomial of a single variable, you'll get a nice, smooth, curvy line with continuity (no holes.)
What are polynomials made of?
A polynomial is an algebraic expression made up of two or more terms. Polynomials are composed of some or all of the following: 1 Variables - these are letters like x, y, and b 2 Constants - these are numbers like 3, 5, 11. They are sometimes attached to variables but are also found on their own. 3 Exponents - exponents are usually attached to variables but can also be found with a constant. Examples of exponents include the 2 in 5² or the 3 in x³. 4 Addition, subtraction, multiplication, and division - For example, you can have 2x (multiplication), 2x+5 (multiplication and addition), and x-7 (subtraction.)
What polynomials cannot contain division?
There are a few rules as to what polynomials cannot contain: Polynomials cannot contain division by a variable. For example, 2y2+7x/4 is a polynomial because 4 is not a variable. However, 2y2+7x/ (1+x) is not a polynomial as it contains division by a variable. Polynomials cannot contain negative exponents. You cannot have 2y-2+7x-4.
What is a polynomial with a degree of two called?
If a polynomial has a degree of two, it is often called a quadratic . If it has a degree of three, it can be called a cubic. Polynomials with degrees higher than three aren't usually named (or the names are seldom used.) You can do numerous operations on polynomials.
How many exponents are there in 5y2x?
The second term (5y2x) has two exponents. They are 2 (from 5y2) and 1 (from x, this is because x is the same as x1.) The exponents in this term add up to three. The last term (4x2) only has one exponent, 2, so its degree is just two. Since the first term has the highest degree (the 4th degree), it is the leading term.
What are the rules for polynomials?
What are the rules for polynomials? The short answer is that polynomials cannot contain the following: division by a variable, negative exponents, fractional exponents, or radicals.
What is polynomial in math?
What are Polynomials? In math, there are some words that are practically foundations to everything else. Just like any topic, math has its own vocabulary and one of the first words you should get comfortable with in algebra is the word “polynomial”.
What does it mean when an exponent is negative?
If an exponent is negative, then this implies you are dividing by that term ( based on the definition of a negative exponent ), and polynomials cannot have any division involving the variables. A polynomial can have fractions involving just the numbers in front of the variables (the coefficients), but not involving the variables.
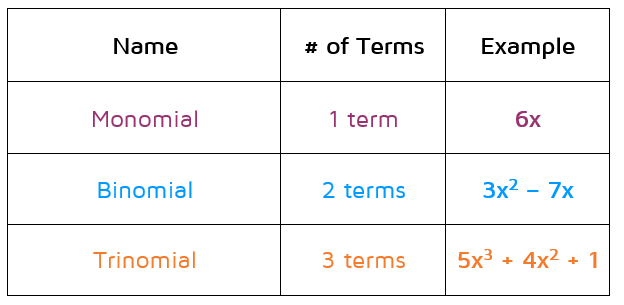
How many variables are in a binomial?
Binomials have two terms. One of the most common types of binomials you will see in algebra are those like 3 x + 5 or x + 4. These involve one variable term and one constant term and are often the factors found when working with quadratic equations.
How many terms are there in a trinomial?
Trinomials have three terms. One place you will see these a lot is the classic “quadratic equation” like 2 x 2 + 5 x + 1 = 0. The expression on the left-hand side of this equation is a trinomial.
What does an exponent mean in math?
In the expression below, this is an illustration of what we mean when we say that an exponent is like multiple multiplications. The exponents signify the number of times that the number 2 should be multiplied by itself.
What is a polynomial?
A polynomial is an equation which is created through the use of two or more algebraic terms. In the example below, each color represents a different term.
What is the difference between multiplying and dividing?
If multiplying numbers with exponents is like adding the exponents together, then dividing is like subtracting the exponents.
Why is the exponent always negative?
No matter what the exponent is in this case, the answer will always be negative because a -1 is being multiplied to whatever number comes out of evaluating the exponent.
How to do scientific notation?
To translate a number into scientific notation, count the number of spaces it would take to get the first non-zero digit to become the one’s digit and then multiply that number by 10 to the number of digits moved. Here we can see an example. We have the number 0.000003. Simply start your pencil at the decimal and then create a bump around each 0 until you get to the other side of the number 3. Then, count the number of bumps. Remember that if you’re translating a big number to be smaller, the exponent next to the 10 should be positive. If you’re translating a small number to be bigger, the exponent next to the 10 should be negative.
What is the power of quotient rule?
The power of a quotient rule is that when a fraction exists within parentheses and is met with an exponent, everything within the parentheses is affected by the exponent. This includes any numbers which are attached to variables as well.
When multiplying monomials by polynomials, is it important to multiply the monomial term by?
When multiplying monomials by polynomials, it’s important to multiply the monomial term by every term within the polynomial.