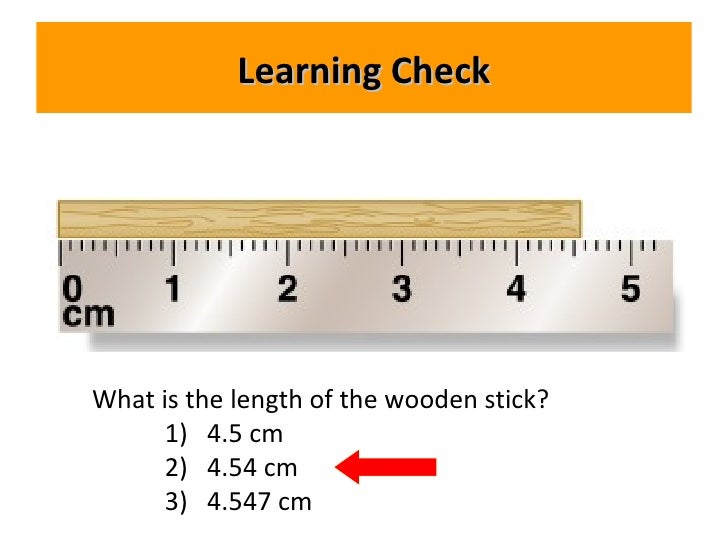
How can significant figures indicate precision? The smaller the measurement increment, the more precise the tool. Significant figures express the precision of a measuring tool. When multiplying or dividing measured values, the final answer can contain only as many significant figures as the least precise value.
How can significant figures indicate precision?
The significant figures of a number are those digits that carry meaning contributing to its precision. Thus the number of significant digits depends on the least count of the measuring instrument. All the certain digits and the one uncertain digit are called the significant figures in the measured value.
Do significant figures show accuracy or precision?
Significant figures express the precision of a measuring tool. When multiplying or dividing measured values, the final answer can contain only as many significant figures as the least precise value.
Does more significant figures mean more precision?
Generally, the significant figures are used to get approximate value. If we use more number of significant figures then the accuracy of final result will increase.
How does significant figures relate to accuracy?
Accuracy refers to how exactly the calculated value matches the right value. Precision refers to how closely individual measurements are in accordance with each other. The number of significant figures is the number of digits considered to be accurate by the person doing the calculation.
How do you know if its accuracy or precision?
Accuracy refers to how close a measurement is to the true or accepted value. Precision refers to how close measurements of the same item are to each other.
How do you know if measurements are precise or accurate?
Accurate measurements are close to the target value but may not be close to each other. Precise measurements are close to each other, whether or not they are close to the target.
What makes a value more precise?
Measurements are precise when you measure the same item multiple times and the values are close to each other.
Which significant figure is least precise?
The rightmost digit of a decimal number is the least significant digit or least significant figure. Another way to look at the least significant figure is to consider it to be the rightmost digit when the number is written in scientific notation. Least significant figures are still significant!
Does more decimals mean more precise?
Roughly speaking, more digits to the right of the decimal point means more precision. The more digits you track on the right of the decimal point, the less you can have on the left of the decimal point.
Does precision or accuracy increase with sample size?
If you increase your sample size you increase the precision of your estimates, which means that, for any given estimate / size of effect, the greater the sample size the more “statistically significant” the result will be.
What does higher precision mean?
Precision can be seen as a measure of quality, and recall as a measure of quantity. Higher precision means that an algorithm returns more relevant results than irrelevant ones, and high recall means that an algorithm returns most of the relevant results (whether or not irrelevant ones are also returned).
What are Significant Figures?
To ensure precision and accuracy in measurements and get reliable data, a fixed method was required to compensate for these uncertainties, leading to significant figures. Here’s an example to understand the difference between precision and accuracy.
Why are significant figures used in analytical concentrations?
Several significant figures are used to indicate the uncertainty of experimental or calculated values. To be able to report analytical concentrations with adequate power-resolution levels, it is important to have the appropriate number of significant data.
What happens when the rightmost digit is greater than 5?
If the rightmost digit to be removed is greater than 5, the preceding number is increased by one. For example, 2.257. If we have to remove 7, we have to round it to 2.26.
How many sig figs are there in 3200?
As we don't have a decimal in 3200, we should start from the right and count significant figures at the first non-zero number (2). Therefore, there are two sig figs in this number (3,2).
What is the first zero that is not present between any two significant figures?
Ans. The first zero that is not present between any two significant figures, and is not present towards the right of the decimals, is not considered significant.
How many significant figures are there in 1432?
For example, in the case of 1432, here we have 4 significant figures and in 0.295, there are three significant figures.
What is the difference between accuracy and precision?
Significant figures were introduced to compensate for the uncertainties in experimental measurements. precision measures how close different measurements are to each other for the same quantity. Accuracy, on the other hand, refers to the agreement of the value of a particular value with the true value of a result.
4 1.3 Accuracy, Precision, and Significant Figures
Determine the appropriate number of significant figures in both addition and subtraction, as well as multiplication and division calculations.
Accuracy and Precision of a Measurement
Science is based on observation and experiment—that is, on measurements. Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard computer paper. The packaging in which you purchased the paper states that it is 11.0 inches long.
Accuracy, Precision, and Uncertainty
The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high.
Precision of Measuring Tools and Significant Figures
An important factor in the accuracy and precision of measurements involves the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, a standard ruler can measure length to the nearest millimeter, while a caliper can measure length to the nearest 0.01 millimeter.
Summary
Accuracy of a measured value refers to how close a measurement is to the correct value. The uncertainty in a measurement is an estimate of the amount by which the measurement result may differ from this value.
Zeros
Special consideration is given to zeros when counting significant figures. The zeros in 0.053 are not significant, because they are only placekeepers that locate the decimal point. There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures.
Example
Determine the number of significant figures in the following measurements:
1. For multiplication and division
The result should have the same number of significant figures as the quantity having the least significant figures entering into the calculation. For example, the area of a circle can be calculated from its radius using A = πr2. A = π r 2. Let us see how many significant figures the area has if the radius has only two—say, r = 1.2 m. r = 1.2 m.
2. For addition and subtraction
The answer can contain no more decimal places than the least precise measurement. Suppose that you buy 7.56-kg of potatoes in a grocery store as measured with a scale with precision 0.01 kg. Then you drop off 6.052-kg of potatoes at your laboratory as measured by a scale with precision 0.001 kg.
What is significant figure?
Significant figures express the precision of a measuring tool.
How to find the precision of a measurement?
The precision of a measurement system refers to how close the agreement is between repeated measurements (which are repeated under the same conditions). Consider the example of the paper measurements. The precision of the measurements refers to the spread of the measured values. One way to analyze the precision of the measurements would be to determine the range, or difference, between the lowest and the highest measured values. In that case, the lowest value was 10.9 in. and the highest value was 11.2 in. Thus, the measured values deviated from each other by at most 0.3 in. These measurements were relatively precise because they did not vary too much in value. However, if the measured values had been 10.9, 11.1, and 11.9, then the measurements would not be very precise because there would be significant variation from one measurement to another.
How is uncertainty related to accuracy?
The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 in., plus or minus 0.2 in. The uncertainty in a measurement, A, is often denoted as δA (“delta A”), so the measurement result would be recorded as A ± δA. In our paper example, the length of the paper could be expressed as 11 in.± 0.2.
What is uncertainty in math?
Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values.
What is accuracy in measurement?
Accuracy of a measured value refers to how close a measurement is to the correct value. The uncertainty in a measurement is an estimate of the amount by which the measurement result may differ from this value.
How many significant figures are in 1300?
There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures. The zeros in 1300 may or may not be significant depending on the style of writing numbers. They could mean the number is known to the last digit, or they could be placekeepers. So 1300 could have two, three, or four significant figures. (To avoid this ambiguity, write 1300 in scientific notation.) Zeros are significant except when they serve only as placekeepers.
What is accuracy in science?
Science is based on observation and experiment—that is, on measurements. Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard computer paper.
How can we find significant figures?
Finding the most precise result using significant figures is quite simple. You can find it manually by calculating the values.
How to get precise results in math?
To get precise results while calculations, it is necessary to find the significant figures of a value. These play an important role to take out exact figures.
What happens if you have zero digits in between?
If you have a long value that has zero digits in between, then that zero digits will be counted as a significant value. We will explain it with an example.
Why is it important to round the generated figures?
It helps to round the generated figures and put an estimated value in our equations that are most accurate and precise.
How many figures do we go through in our daily life?
In our daily life, we go through hundreds of figures while we calculate the values.
Do you put significant figures after decimal?
Although, the values after decimal don’t play such a role in the calculation, when we need a precise result, then significant figures are quite important.
Can you take help from calculators?
Also, you can take help from online calculators that make the working easy and provide you the significant figures in entire value.
How to find the precision of a measurement?
The precision of a measurement system refers to how close the agreement is between repeated measurements (which are repeated under the same conditions). Consider the example of the paper measurements. The precision of the measurements refers to the spread of the measured values. One way to analyze the precision of the measurements would be to determine the range, or difference, between the lowest and the highest measured values. In that case, the lowest value was 10.9 in. and the highest value was 11.2 in. Thus, the measured values deviated from each other by at most 0.3 in. These measurements were relatively precise because they did not vary too much in value. However, if the measured values had been 10.9, 11.1, and 11.9, then the measurements would not be very precise because there would be significant variation from one measurement to another.
When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can?
When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value. There are two different rules, one for multiplication and division and the other for addition and subtraction, as discussed below.
Why are the zeros in 0.053 not significant?
The zeros in 0.053 are not significant, because they are only placekeepers that locate the decimal point. There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures.
What is the uncertainty of a stopwatch?
A high school track coach has just purchased a new stopwatch. The stopwatch manual states that the stopwatch has an uncertainty of ±0.05 s. The team's top sprinter clocked a 100 meter sprint at 12.04 seconds last week and at 11.96 seconds this week. Can we conclude that this week's time was faster?
How is uncertainty related to accuracy?
The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 in., plus or minus 0.2 in. The uncertainty in a measurement,#N#A A#N#size 12 {A} {}, is often denoted as#N#δA δA#N#size 12 {δA} {} (“delta#N#A A#N#size 12 {A} {} ”), so the measurement result would be recorded as#N#A ± δA A ± δA#N#size 12 { +- δA } {}. In our paper example, the length of the paper could be expressed as#N#11 in. ± 0. 2. 11 in. ± 0. 2.#N#size 12 { +- 0 "." 2 "." } {}
How many significant figures are in 1300?
There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures. The zeros in 1300 may or may not be significant depending on the style of writing numbers. They could mean the number is known to the last digit, or they could be placekeepers. So 1300 could have two, three, or four significant figures. (To avoid this ambiguity, write 1300 in scientific notation.) Zeros are significant except when they serve only as placekeepers.
What are some examples of uncertainty?
In our example, such factors contributing to the uncertainty could be the following: the smallest division on the ruler is 0.1 in., the person using the ruler has bad eyesight, or one side of the paper is slightly longer than the other. At any rate, the uncertainty in a measurement must be based on a careful consideration of all the factors that might contribute and their possible effects.
1.3 Accuracy, Precision, and Significant Figures
Determine the appropriate number of significant figures in both addition and subtraction, as well as multiplication and division calculations.
Accuracy and Precision of a Measurement
Science is based on observation and experiment—that is, on measurements. is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard computer paper. The packaging in which you purchased the paper states that it is 11.0 inches long.
Accuracy, Precision, and Uncertainty
The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high.
Precision of Measuring Tools and Significant Figures
An important factor in the accuracy and precision of measurements involves the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, a standard ruler can measure length to the nearest millimeter, while a caliper can measure length to the nearest 0.01 millimeter.
Summary
Accuracy of a measured value refers to how close a measurement is to the correct value. The uncertainty in a measurement is an estimate of the amount by which the measurement result may differ from this value.

What Are Significant Figures?
- To ensure precision and accuracy in measurements and get reliable data, a fixed method was required to compensate for these uncertainties, leading to significant figures. Here’s an example to understand the difference between precision and accuracy. In the above example, the true value of an experiment is 3.00g. Students 'A' take two measurements, ...
Addition and Subtraction of Significant Figures
- The result cannot have more digits to the right of the decimal point than either of the original numbers. Here 10.0 has only one digit to the right of the decimal point. Therefore the result should also have only one digit after the decimal point. So the answer is 37.2. 359.62 - 67.3 = 292.3 In this case, 359.62 has two digits after the decimal point and 67.3 has one digit right to the decim…
Multiplication and Division of Significant Figures
- In this case, the result must not have more significant figures than the original numbers used in the measurement with few significant figures. 3.52.12= 7.42 Since 3.5 has two significant figures, the result should not exceed significant figures more than two. Therefore the answer is 7.4.
Pacific Rule and Atlantic Rule
- Pacific Rule should be applied to numbers that have decimal Present (note the double P). Start at the left side of the number, since the Pacific Ocean is on the left side of the United States. Count the significant figures starting at the first non-zero number and continuing to the end. As an example, start from the left side of 0.000530 because it contains a decimal. The number of signi…
Things to Remember
- To round off the numbers, one must consider the following points for limiting the result to the required number of significant figures as per the above mathematical operations:
- If the rightmost digit to be removed is greater than 5, the preceding number is increased by one. For example, 2.257. If we have to remove 7, we have to round it to 2.26.
- The preceding number is not changed if the rightmost digit to be removed is less than 5. For …
- To round off the numbers, one must consider the following points for limiting the result to the required number of significant figures as per the above mathematical operations:
- If the rightmost digit to be removed is greater than 5, the preceding number is increased by one. For example, 2.257. If we have to remove 7, we have to round it to 2.26.
- The preceding number is not changed if the rightmost digit to be removed is less than 5. For example, 5.342 if 2 is to be removed, then the result is rounded up to 5.34.
- When removing the rightmost digit, if it is 5, the preceding number stays the same if the number is even, but is increased by one if it is odd. For example, if 7.35 is to be rounded by removing 5,...