
The differentiation rules are listed as follows:
- Sum Rule: If y = u (x) ± v (x), then dy/dx = du/dx ± dv/dx.
- Product Rule: If y = u (x) × v (x), then dy/dx = u.dv/dx + v.du/dx
- Quotient Rule: If y = u (x) ÷ v (x), then dy/dx = (v.du/dx- u.dv/dx)/ v 2
- Power Rule: (d/dx) (xn ) = nxn-1
- Derivative of a constant, a: (d/dx) (a) = 0.
- Derivative of a constant multiplied with function f: (d/dx) (a. f) = af'
- Sum Rule: (d/dx) (f ± g) = f' ± g'
- Product Rule: (d/dx) (fg)= fg' + gf'
- Quotient Rule: d d x ( f g ) = g f ′ – f g ′ g 2.
How do you differentiate an equation?
- For example, let's say that we're trying to differentiate x 3 z 2 - 5xy 5 z = x 2 + y 3.
- First, let's differentiate with respect to x and insert (dz/dx). Don't forget to apply the product rule where appropriate! ...
- Now, let's do the same for (dz/dy) x 3 z 2 - 5xy 5 z = x 2 + y 3 2x 3 z (dz/dy) - 25xy 4 z - ...
What does differentiate mean math?
To differentiate means to find the slope at a point. Let’s say you have a function that models where a car is at any particular point in time. If you differentiate that position function, you end up with a velocity function.
How to differentiate an equation?
Differential equations have a derivative in them. For example, dy/dx = 9x. In elementary algebra, you usually find a single number as a solution to an equation, like x = 12. But with differential equations, the solutions are functions.In other words, you have to find an unknown function (or set of functions), rather than a number or set of numbers as you would normally find with an equation ...
How do you differentiate in math?
Before differentiating:
- Remove brackets
- Separate 'top heavy' fractions
- Change terms involving roots into fractional powers
- Change terms with \ (x\) on the denominator to negative powers

How do you differentiate equations?
Differentiation FormulasIf f(x) = tan (x), then f'(x) = sec2x.If f(x) = cos (x), then f'(x) = -sin x.If f(x) = sin (x), then f'(x) = cos x.If f(x) = ln(x), then f'(x) = 1/x.If f(x) = ex, then f'(x) = exIf f(x) = xn, where n is any fraction or integer, then f'(x) = nxn-1More items...•
How do you differentiate functions?
0:014:46How to differentiate a function - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe have to multiply x by the power which is two. So we would write d y by dx which is theMoreWe have to multiply x by the power which is two. So we would write d y by dx which is the differential.
What are the 7 rules of differentiation?
The differentiation rules help us to evaluate the derivatives of some particular functions, instead of using the general method of differentiation....Differentiation RulesPower Rule.Sum and Difference Rule.Product Rule.Quotient Rule.Chain Rule.
What is the derivative of a formula?
Definition 2.4. 1 The derivative of a function f, denoted f′, is f′(x)=limΔx→0f(x+Δx)−f(x)Δx. We know that f′ carries important information about the original function f.
What are 5 ways to differentiate instruction?
Here are five ways you can differentiate instruction in your classroom.Include Every Learning Style. ... Offer Assignment Options. ... Establish Learning Stations. ... Plan Tiered Lessons. ... Organize Students in Groups.
What are examples of differentiated activities?
Examples of differentiating activities: Match vocabulary words to definitions. Read a passage of text and answer related questions. Think of a situation that happened to a character in the story and a different outcome. Differentiate fact from opinion in the story.
What are the 3 derivative rules?
3 Rules for Finding DerivativesThe Power Rule.Linearity of the Derivative.The Product Rule.The Quotient Rule.The Chain Rule.
What is the differentiation of 2x?
Differentiation of 2x Using Power Rule Therefore, we have d(2x)/dx = 2 dx/dx = 2. Hence, the differentiation of 2x is equal to 2.
What is the derivative of 3x?
0:250:56Derivative of 3x - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo for this example. We have 3x so our constant is 3 that is our derivative.MoreSo for this example. We have 3x so our constant is 3 that is our derivative.
What are the 4 types of differential equations?
Types of Differential EquationsOrdinary Differential Equations.Partial Differential Equations.Linear Differential Equations.Nonlinear differential equations.Homogeneous Differential Equations.Nonhomogeneous Differential Equations.
What is the difference between D and DX DX?
1:134:09What is the Difference Between dy/dx and d/dx - YouTubeYouTubeStart of suggested clipEnd of suggested clipBasically means that you're taking the derivative of a function f f of X and so this little dashMoreBasically means that you're taking the derivative of a function f f of X and so this little dash means that you're taking the derivative of that and this is Newton's notation.
How do you differentiate a function and not a function?
A function is a relation between domain and range such that each value in the domain corresponds to only one value in the range. Relations that are not functions violate this definition. They feature at least one value in the domain that corresponds to two or more values in the range.
How do you differentiate a function with two variables?
To find fx we differentiate as normal taking x as the variable and y as the constant. Remember that when we differentiate a constant times a function of x we differentiate the function of x as normal and then multiply it by the constant. For example, 3x2 differentiates to give 3(2x)=6x.
What are the formulas of differentiation?
The formulas of differentiation that helps in solving various differential equations include: Derivatives of basic functions Derivatives of Logar...
What are the basic rules of differentiation?
The basic rule of differentiation are: Power Rule: (d/dx) (x n ) = nx {n-1} Sum Rule: (d/dx) (f ± g) = f’ ± g’ Product Rule: (d/dx) (fg)= fg’ +...
What are the derivatives of trigonometric functions?
The derivatives of six trigonometric functions are: (d/dx) sin x = cos x (d/dx) cos x = -sin x (d/dx) tan x = sec 2 x (d/dx) cosec x = -cosec...
What is d/dx?
The general representation of the derivative is d/dx. This denotes the differentiation with respect to the variable x.
What is a UV formula?
(d/dx)(uv) = v(du/dx) + u(dv/dx) This formula is used to find the derivative of the product of two functions.
1. What are the fundamental rules of differentiation?
The basic differentiation rules are explained as follows:Sum and Difference Rule is the rule which is used to determine the sum or difference of tw...
2. What role do differentiation play in real life?
Importance of differentiation in day-to-day life can not be ignored. It solves many calculations in daily life. It is used to find the maximum and...
3. What are the tips to master the topic of differentiation?
Differentiation is the basic foundation of calculus. If one can master the topic then he or she can be confident enough to face any competitive exa...
4. What are the interesting facts about differentiation?
Differential formulas and equations are quite interesting. Differentiation has the potential to make science more descriptive and not a difficult e...
5. Which books are best for differential equations?
Ordinary Differential Equations by Tenenbaum is the best book to start with since it not only uses an easy approach to make the concept lucid but a...
What is differential in math?
Differentiation can be defined as a derivative of independent variable value and can be used to calculate features in an independent variable per unit modification.
What are the functions of x and differentiated with respect to x?
Both f and g are the functions of x and differentiated with respect to x.
What is the method of evaluating a function's derivative at any time?
Differentiation is the method of evaluating a function's derivative at any time.
When is f the function derivative?
When f (x) is the sum of two u (x) and v (x) functions, it is the function derivative,
Is the rate of feature shift the same as the level of function change?
A linear function varies by its domain at a constant rate. Therefore, the overall rate of feature shift is the same as the level of function change in any situation. Nevertheless, in the case of non-linear processes, the rate of change ranges from point to point.
How many types of differentiation rules are there?
There are mainly 7 types of differentiation rules that are widely used to solve problems relate to differentiation:
What is differential in math?
Differentiation is a process of calculating a function that represents the rate of change of one variable with respect to another. Differentiation and derivatives have immense application not only in our day-to-day life but also in higher mathematics.
What is differentiation in class 11?
Differentiation Formulas: Differentiation is one of the most important topics for Class 11 and 12 students. There are a lot of higher-level concepts of differentiation that are taught in colleges.
How to differentiate sums?
In other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then put them back together with the appropriate signs. Note as well that this property is not limited to two functions.
How to find rate of change of a function?
We know that the rate of change of a function is given by the functions derivative so all we need to do is it rewrite the function (to deal with the second term) and then take the derivative.
What is the derivative of a constant?
The derivative of a constant is zero. See the Proof of Various Derivative Formulas section of the Extras chapter to see the proof of this formula.
When you see radicals, should you first convert the radical to a fractional exponent?
There is a general rule about derivatives in this class that you will need to get into the habit of using. When you see radicals you should always first convert the radical to a fractional exponent and then simplify exponents as much as possible. Following this rule will save you a lot of grief in the future.
Why do we need derivatives?
We need the derivative in order to get the velocity of the object. The derivative, and hence the velocity, is,
Is derivative a product or quotient of two functions?
The derivative of a product or quotient of two functions is not the product or quotient of the derivatives of the individual pieces. We will take a look at these in the next section.
Can you combine exponents in the last two terms?
In the last two terms we combined the exponents. You should always do this with this kind of term. In a later section we will learn of a technique that would allow us to differentiate this term without combining exponents, however it will take significantly more work to do. Also, don’t forget to move the term in the denominator of the third term up to the numerator. We can now differentiate the function.
What are the different rules of differentiation?
There are different rules followed in differentiating a function. The differentiation rules are power rule, chain rule, quotient rule, and the constant rule.
How is differentiation done?
Differentiation is done by applying the techniques of known differentiation formulas and differentiation rules in finding the derivative of a given function.
What is the process of finding derivatives of a function called?
The process of finding derivatives of a function is called differentiation in calculus. A derivative is the rate of change of a function with respect to another quantity. The laws of Differential Calculus were laid by Sir Isaac Newton. The principles of limits and derivatives are used in many disciplines of science. Differentiation and integration form the major concepts of calculus. Let us learn the techniques of differentiation to find the derivatives of algebraic functions, trigonometric functions, and exponential functions.
How to find derivative of function?
The derivative of a function is found by applying limits to the function as per the first principle of differentiation. The derivative f' (x) = lim Δx→0 f (x+Δx) −f (x) Δx lim Δ x → 0
What is the instantaneous rate of change of a function with respect to another quantity called?
The instantaneous rate of change of a function with respect to another quantity is called differentiation. For example, speed is the rate of change of displacement at a certain time. If y = f (x) is a differentiable function of x, then dy/dx = f' (x) = lim Δx→0 f (x+Δx) −f (x) Δx lim Δ x → 0
What is the ratio of a small change in one quantity with a small change in another which is dependent on the?
The ratio of a small change in one quantity with a small change in another which is dependent on the first quantity is called differentiation. One of the important concepts in calculus is mainly focused on the differentiation of a function. The maximum or minimum value of a function, the velocity and acceleration of moving objects, and the tangent of a curve are determined by differentiation. If y = f (x) that is differentiable, then the differentiation is represented as f' (x) or dy/dx.
What is the derivative of a constant function?
The derivative of a constant function is 0. if y = k, where k is a constant, then y' = 0
What is the % Difference Formula?
The % Difference Formula allows us to find the percentage difference between two numbers with either of the numbers used as the base number. The % difference formula takes as input two numbers – the base number and the new number – and gives as output the percentage difference between the new number and the base number. The formula will output different results depending on which number is chosen as the base number and which number is chosen as the new number.
What is data validation in Excel?
Data Validation in Excel Data validation in Excel is an existing and accessible tool to ensure data integrity while building a financial model. It helps secure your model inputs and outputs.
How to differentiate x to the power of something?
Therefore to differentiate x to the power of something you bring the power down to in front of the x, and then reduce the power by one.
How does differentiation help us?
Differentiation allows us to find rates of change. For example, it allows us to find the rate of change of velocity with respect to time (which is acceleration). It also allows us to find the rate of change of x with respect to y, which on a graph of y against x is the gradient of the curve. There are a number of simple rules which can be used to allow us to differentiate many functions easily.
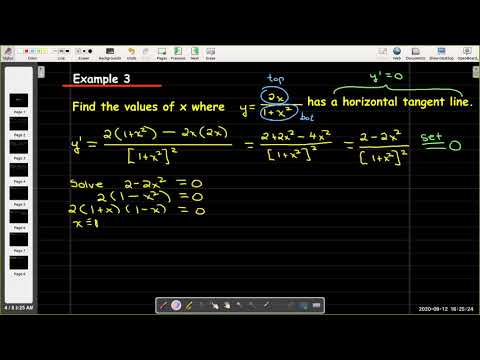
Rules of Differentiation: Differentiation Formulas Pdf
Differentiation Formulas List
- The table below provides the derivatives of basic functions, constant, a constant multiplied with a function, power rule, sum and difference rule, product and quotient rule, etc. Differentiation formulas of basic logarithmic and polynomial functions are also provided. Let us now look into the differentiation formulas for different types of functions.
Differentiation Formulas For Trigonometric Functions
- Sine (sin), cosine (cos), tangent (tan), secant (sec), cosecant (cosec), and cotangent (cot) are the six commonly used trigonometric functions each of which represents the ratio of two sides of a triangle. The derivatives of trigonometric functions are as under:
Differentiation Formulas For Inverse Trigonometric Functions
- Inverse trigonometric functions like (\(\sin^{-1}~ x)\) , (\(\cos^{-1}~ x)\) , and (\(\tan^{-1}~ x)\) represents the unknown measure of an angle (of a right angled triangle) when lengths of the two sides are known. The derivatives of inverse trigonometric functions are as under:
Formulas For Hyperbolic Functions Differentiation
- The hyperbolic function of an angle is expressed as a relationship between the distances from a point on a hyperbola to the origin and to the coordinate axes. The derivatives of hyperbolic functions are as under: Practice Exam Questions So, now you are aware of the differentiation formulas, i.e. derivatives of popular trigonometric, polynomial, inverse trigonometric, logarithmic…
FAQs on Differentiation Formulas Class 12
- You can find the important FAQs answered by our experts below: Students can make use of NCERT Solutionsfor Maths provided by Embibe for their exam preparation. Free Practice Questions and Mock Tests for Maths (Class 8 to 12) We hope that this complete list of differentiation formulas helps you. If you have any questions, feel free to ask in the comment se…