If you follow these steps, solving rational inequalities is a piece of cake:
- Rearrange the inequality so that only 0 remains on the right side. ...
- Create one fraction on the left side, if necessary. ...
- Factor the numerator and denominator. ...
- Set each factor in the numerator equal to 0 and solve. ...
- Set each factor in the denominator equal to 0 and solve. ...
- Choose test points to find soltion intervals. ...
What is the easiest way to solve inequalities?
What are the rules of solving inequalities?
- Add the same number on both sides.
- From both sides, subtract the same number.
- By the same positive number, multiply both sides.
- By the same positive number, divide both sides.
- Multiply the same negative number on both sides and reverse the sign.
What steps do you use to solve rational equations?
The steps to solve a rational equation are:
- Find the common denominator.
- Multiply everything by the common denominator.
- Simplify.
- Check the answer (s) to make sure there isn't an extraneous solution.
What are the steps in solving rational equations?
Solve equations with rational expressions. Step 1. Note any value of the variable that would make any denominator zero. Step 2. Find the least common denominator of all denominators in the equation. Step 3. Clear the fractions by multiplying both sides of the equation by the LCD. Step 4. Solve the resulting equation. Step 5. Check:
What are the steps to solving equations and inequalities?
The steps for solving inequalities are the same as those for solving equations:
- Remove parentheses
- Collect like terms on each side of the inequality symbol
- Get the variables together on one side
- Isolate the variable
- Check

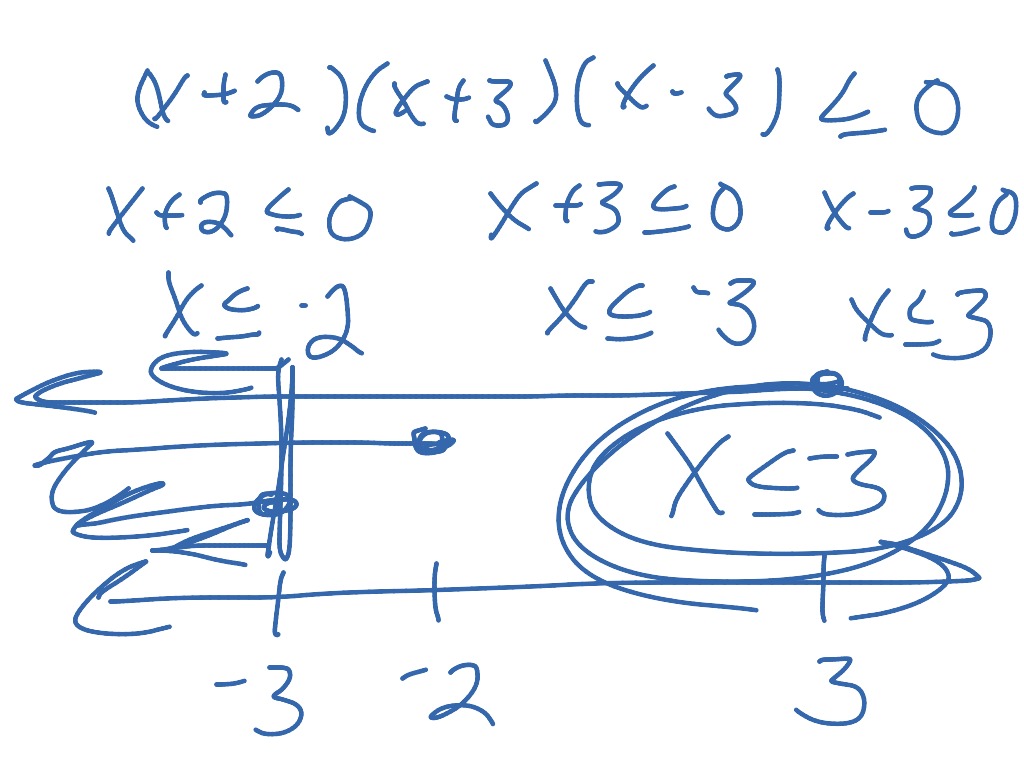
How do you solve a rational inequality?
To solve a rational inequality, we follow these steps:Put the inequality in general form.Set the numerator and denominator equal to zero and solve. ... Plot the critical values on a number line, breaking the number line into intervals.Take a test number from each interval and plug it into the original inequality.More items...•
What is the first step in solving rational inequality?
To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right. Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.
What are 5 examples of rational inequality?
A rational inequality is an inequality that contains a rational expression. Inequalities such as 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , and 1 4 − 2 x 2 ≤ 3 x 1 4 − 2 x 2 ≤ 3 x are rational inequalities as they each contain a rational expression.
What are the steps in solving a rational equation and inequality?
The steps to solve a rational equation are: Find the common denominator. Multiply everything by the common denominator. Simplify.
How do you solve rational equations?
How to: Solve a Rational Equation.Factor all denominators to determine the LCD. Note the restrictions to x. ... Multiply both sides of the equal sign by the LCD. Every term in the equation is multiplied by the LCD. ... Solve the resulting equation.Check for extraneous solutions.
What is the formula for rational equation?
A rational equation is an equation containing at least one fraction whose numerator and denominator are polynomials, \frac{P(x)}{Q(x)}. Q(x)P(x). These fractions may be on one or both sides of the equation.
What is rational inequality in math?
A rational inequality is an inequality which contains a rational expression. The trick to dealing with rational inequalities is to always work with zero on one side of the inequality. Re-write the problem if necessary to obtain a zero on one side!
What is the symbol of rational inequality?
InequalitiesSymbolWordsExample>greater than(x+1)/(3−x) > 2
Definitions: A rational expression is the ratio of two polynomials. If f is a rational expression then f can be written in the form p/q where p and q are polynomials.
The first step in solving rational equations is to transform the equation into a polynomial equation. This is accomplished by clearing the fraction which means multiplying the entire equation by the common denominator of all the rational expressions.
To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right. Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.
This rational inequality is already in standard form. Step 2: Factor the numerator and denominator and find the values of x that make these factors equal to 0 to find the boundary points. -5 and 1 are boundary points. Step 3: Use the boundary point(s) found in step 2 to mark off test intervals on the number line.
1:277:29Solving Rational Exponents and Radical Inequalities - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo i know that eight is really two cubed. So you can see that i have four groups of three. And oneMoreSo i know that eight is really two cubed. So you can see that i have four groups of three. And one two from each group escapes. So i get 2x equals 16 which means that x equals 8.
A rational inequality is an inequality which contains a rational expression. The trick to dealing with rational inequalities is to always work with zero on one side of the inequality. Re-write the problem if necessary to obtain a zero on one side!
Answer: A rational inequality is an inequality which consists of a rational expression. While solving a rational inequality, we can use distinct me...
Answer: When we solve an equation and the outcome is x=7, we are known that there is only one solution, which is 7.On the other hand, when we solve...
Answer: A critical point is a number that makes the rational expression zero (0) or undefined.
When solving a rational inequality, we must first write the inequality with 0 on the right and only one quotient on the left.
Step 1: Write the expression of inequality as one quotient on the left and zero (0) on the right. Step 2: identify the critical points–the points where the rational expression will either be undefined or zero. Step 3: Use the critical points for dividing the number line into intervals. Step 4: Test the value of each interval.
A key approach towards solving rational inequalities depends upon determining the critical values of the rational expression that divides the number line into distinctive open intervals. The critical values are the zeros (0s) of both the numerator as well as the denominator. Note that the zeros of the denominator make the rational expression ...
Struggling with the ways of how to find rational inequalities? Well! There are different ways of solving rational inequalities which are as below: 1 Solving rational inequalities algebraically. 2 Solving inequalities with rational expressions. 3 Solving rational inequalities by graphing.
Critical points are identified for using them to divide the number line into intervals. Once identifying the critical points, factors of the numerator and denominator, and quotient in each interval are found. This will identify the interval, or intervals, which consists of all the solutions of rational inequality.
While solving a rational inequality, we can use distinct methods as we use when solving linear inequalities. We particularly must remember that when we multiply or divide by a negative number, the inequality sign should reverse.
If you observe, the only interval providing a true statement is (- 1, 4) .
So, we need regions that make the rational expression negative. That means the middle region . Also, since we’ve got an “or equal to” part in the inequality we also need to include where the inequality is zero, so this means we include x = − 1 x = − 1. Notice that we will also need to avoid x = 5 x = 5 since that gives division by zero.
Once again, it’s important to note that we really do need to test each region and not just assume that the regions will alternate in sign.
A rational inequality is a kind of mathematical inequality statement that contains a ratio of two polynomials (also called a ~'rational expression~'), usually on the left-hand side of the inequality, with a zero commonly on the right-hand side. Discover the rational inequality, learn how to solve one for its critical values, and investigate how to write a solution using interval notation. Updated: 11/23/2021
Take a test number from each interval and plug it into the original inequality. If it makes a true statement, then the interval from which it came is in the solution. If it makes a false statement, then the interval from which it came is not in the solution.
We see that the intervals that make our inequality a true statement are from -30 to 0 and from 30 to infinity.
The values you get are called critical values. The critical values of a function are where the function is undefined or equal to 0. When the numerator is 0, the function is 0. When the denominator is 0, the function is undefined.
Since you can't sell a negative number of bicycles, we can disregard the interval (-30, 0). This tells us that to make a profit, you need to sell more than 30 bicycles - better get started!
When dealing with inequalities, if we multiply both sides by a negative number, we must switch the direction of the inequality symbol. Since the denominator contains a variable, we don't know if it will be positive or negative, so we don't know if we need to switch the direction of the symbol. Thus, in rational inequalities, we can't eliminate the denominators by multiplying both sides by an expression containing a variable.
Enrolling in a course lets you earn progress by passing quizzes and exams.
Multiplying or dividing by a negative will change the signs of both sides, and thus change the relative positions of the numbers on the number line, effectively mirroring them about zero. So, if you have 2 > 1, and multiply by a -1, you get -2 > -1, which is not true, since -1 is more positive.
Keep in mind that a "value" being greater or less than another value refers to its position on the number line: those with lesser values are "more negative," or further left on the number line, while those with greater values are "more positive," or further to the right on the number line.
Use that and put in the reciprocal of the order of the root. For a fifth root that would be 1/5 or 0.2. A root is really a reciprocal of the power. So a square root is really the same as raising to the power of one half and a fifth root is the same as raising to the power of 1/5 or 0.2.
What is a rational expression in math?
What is the first step in solving a rational equation?
Which Below is the first step in solving the rational inequality Brainly?
What is the third step in solving rational inequality?
How do you solve rational inequalities with exponents?
What is considered rational inequality?
Q1. What is a Rational Inequality?
Q2. What is the Difference Between a Linear Equation and a Rational Inequality?
Q3. What is a Critical Point?
Did You Know?
How to write an inequality?
What are the critical values of rational expressions?
How to solve rational inequalities?
What is critical point?
When solving a rational inequality, can we use distinct methods?
What is the only interval that provides a true statement?
What region of the rational expression is negative?
Do we need to test each region?
What is rational inequality?
How to find the interval from which it came in the inequality?
What intervals make inequality true?
What is the critical value of a function?
How many bicycles do you need to sell to make a profit?
When dealing with inequalities, do we have to switch the direction of the inequality symbol?
What does it mean to enroll in a course?
What happens when you multiply by a negative?
What does it mean when a value is greater than another?
What is the reciprocal of a fifth root?
Popular Posts: