In summary, three steps are required to perform the vector addition using the parallelogram method:
- Step 1: Place the two vectors so that they have a common starting point
- Step 2: Draw and complete the parallelogram using copies of the two original vectors
- Step 3: The diagonal of the parallelogram is then equal to the sum of the two vectors
What are the methods in vector addition?
Vector addition is one of the most common vector operations that a student of physics must master. When adding vectors, a head-to-tail method is employed. The head of the second vector is placed at the tail of the first vector and the head of the third vector is placed at the tail of the second vector; and so forth until all vectors have been added.
What is the formula for vector addition?
What is the formula for vector addition? To add or subtract two vectors, add or subtract the corresponding components. Let →u’=’ u1,u2 and →v’=’ v1,v2 be two vectors. The sum of two or more vectors is called the resultant. The resultant of two vectors can be found using either the parallelogram method or the triangle method .
How do you add vectors using the component method?
Key Points
- To add vectors, lay the first one on a set of axes with its tail at the origin. ...
- To subtract vectors, proceed as if adding the two vectors, but flip the vector to be subtracted across the axes and then join it tail to head as if adding.
- Adding or subtracting any number of vectors yields a resultant vector.
How to set a vector?
- Get the vector.
- Define a set which copies all elements of the vector using 2 pointers begin and end.
- Print the set.
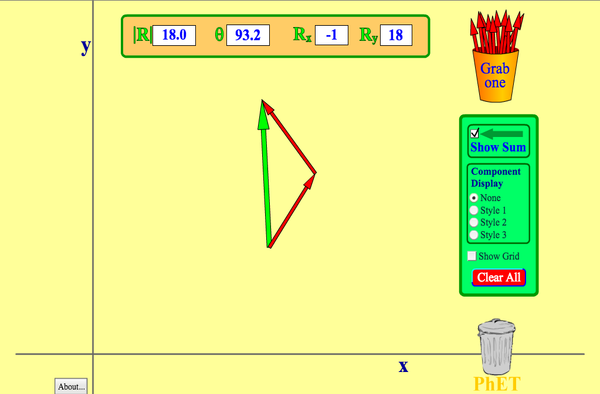
What is the Vector Addition?
Vectors are represented as a combination of direction and magnitude and are written with an alphabet and an arrow over them (or) with an alphabet written in bold. Two vectors, a and b, can be added together using vector addition, and the resultant vector can be written as: a + b. Before learning about the properties of vector addition, we need to know about the conditions that are to be followed while adding vectors. The conditions are as follows:
How to add vectors?
This is the formula for the addition of vectors: Given two vectors →a a → and →b b → , then the magnitude of the resultant sum vector →M M → = | →M M → | = √ ( ( M x M x )2+ ( M y M y )2) . And the angle can be computed as θ = tan-1 ( M y M y / M x M x)
How do you add vectors together?
The triangle law of the addition of vectors states that two vectors can be added together by placing them together in such a way that the first vector’s head joins the tail of the second vector. Thus, by joining the first vector’s tail to the head of the second vector, we can obtain the resultant sum vector.
How are vectors placed together?
First, the two vectors →M M → and →N N → are placed together in such a manner that the head of vector →M M → connects the tail of vector →N N →.
What is vector representation?
Vectors are represented as a combination of direction and magnitude and they are drawn with an arrow representation.
How to determine the components of a vector?
Mathematically, using the magnitude and the angle of the given vector, we can determine the components of a vector.
What is the law of adding vectors?
Triangle Law of Addition of Vectors. The famous triangle law can be used for the addition of vectors and this method is also called the head-to-tail method. As per this law, two vectors can be added together by placing them together in such a way that the first vector’s head joins the tail of the second vector.
How to find the direction of a vector?
Once the measure of the angle is determined , the direction of the vector can be found. In this case the vector makes an angle of 45 degrees with due East. Thus, the direction of this vector is written as 45 degrees. (Recall from earlier in this lesson that the direction of a vector is the counterclockwise angle of rotation that the vector makes with due East.)
How to determine the direction of a resultant vector?
The direction of a resultant vector can often be determined by use of trigonometric functions. Most students recall the meaning of the useful mnemonic SOH CAH TOA from their course in trigonometry. SOH CAH TOA is a mnemonic that helps one remember the meaning of the three common trigonometric functions - sine, cosine, and tangent functions. These three functions relate an acute angle in a right triangle to the ratio of the lengths of two of the sides of the right triangle. The sine function relates the measure of an acute angle to the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine function relates the measure of an acute angle to the ratio of the length of the side adjacent the angle to the length of the hypotenuse. The tangent function relates the measure of an angle to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. The three equations below summarize these three functions in equation form.
How to draw a vector head to tail?
The head-to-tail method involves drawing a vector to scale on a sheet of paper beginning at a designated starting position. Where the head of this first vector ends, the tail of the second vector begins (thus, head-to-tail method). The process is repeated for all vectors that are being added. Once all the vectors have been added head-to-tail, the resultant is then drawn from the tail of the first vector to the head of the last vector; i.e., from start to finish. Once the resultant is drawn, its length can be measured and converted to real units using the given scale. The direction of the resultant can be determined by using a protractor and measuring its counterclockwise angle of rotation from due East.
Why are summing vectors applied to free body diagrams?
These rules for summing vectors were applied to free-body diagrams in order to determine the net force (i.e., the vector sum of all the individual forces). Sample applications are shown in the diagram below.
How to find the magnitude of vectors?
The magnitude and direction of the sum of two or more vectors can also be determined by use of an accurately drawn scaled vector diagram. Using a scaled diagram, the head-to-tail method is employed to determine the vector sum or resultant. A common Physics lab involves a vector walk. Either using centimeter-sized displacements upon a map or meter-sized displacements in a large open area, a student makes several consecutive displacements beginning from a designated starting position. Suppose that you were given a map of your local area and a set of 18 directions to follow. Starting at home base, these 18 displacement vectors could be added together in consecutive fashion to determine the result of adding the set of 18 directions. Perhaps the first vector is measured 5 cm, East. Where this measurement ended, the next measurement would begin. The process would be repeated for all 18 directions. Each time one measurement ended, the next measurement would begin. In essence, you would be using the head-to-tail method of vector addition.
How to scale a vector in a diagram?
Pick a starting location and draw the first vector to scale in the indicated direction. Label the magnitude and direction of the scale on the diagram (e.g., SCALE: 1 cm = 20 m).
Where do you draw the resultant?
Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector as Resultant or simply R.
What is vector addition?
The Graphical Method of Vector Addition and Subtraction. Recall that a vector is a quantity that has magnitude and direction. For example, displacement, velocity, acceleration, and force are all vectors. In one-dimensional or straight-line motion, the direction of a vector can be given simply by a plus or minus sign.
How many graphical representations of vector addition?
This video shows four graphical representations of vector addition and matches them to the correct vector addition formula.
How to subtract vectors?
Vector subtraction is done in the same way as vector addition with one small change. We add the first vector to the negative of the vector that needs to be subtracted. A negative vector has the same magnitude as the original vector, but points in the opposite direction (as shown in Figure 5.6 ). Subtracting the vector B from the vector A, which is written as A − B, is the same as A + (− B ). Since it does not matter in what order vectors are added, A − B is also equal to (− B) + A. This is true for scalars as well as vectors. For example, 5 – 2 = 5 + (−2) = (−2) + 5.
How do vectors work in two dimensions?
In a one-dimensional problem, one of the components simply has a value of zero. For two-dimensional vectors, we work with vectors by using a frame of reference such as a coordinate system. Just as with one-dimensional vectors, we graphically represent vectors with an arrow having a length proportional to the vector’s magnitude and pointing in the direction that the vector points.
What is the direction of a vector?
In one-dimensional or straight-line motion, the direction of a vector can be given simply by a plus or minus sign. Motion that is forward, to the right, or upward is usually considered to be positive (+); and motion that is backward, to the left, or downward is usually considered to be negative (−).
Does head to tail add vectors?
The head-to-tail graphical method of vector addition works for any number of vectors. It is also important to note that it does not matter in what order the vectors are added. Changing the order does not change the resultant. For example, we could add the vectors as shown in Figure 5.12, and we would still get the same solution.
Where are vectors placed in Figure 5.15?
Figure 5.15 The vectors are placed head to tail.
How to add two vectors?
Two vectors a and b represented by the line segments can be added by joining the ‘tail’ of vector b to the ‘nose’ of vector a . Alternatively, the ‘tail’ of vector a can be joined to the ‘nose’ of vector b.
What is the rule for vector addition?
In vector addition, the intermediate letters must be the same. Since PQR forms a triangle, the rule is also called the triangle law of vector addition. Graphically we add vectors with a “head to tail” approach. The addition of vectors using the head-to-tail method.
How are vectors added?
Vectors are added by adding the corresponding components.
When adding two vectors, what is the biggest resultant possible?
When adding two vectors, the biggest resultant possible is when the vectors are parallel.
Is vector addition commutative?
We will find that vector addition is commutative, that is a + b = b + a
Tips & Thanks
Posted 10 years ago. Direct link to Prathamesh's post “In the above example, R1 ...”
Video transcript
In the last video I was a little formal in defining what Rn is, and what a vector is, and what vector addition or scalar multiplication is. In this video I want to kind of go back to basics and just give you a lot of examples. And give you a more tangible sense for what vectors are and how we operate with them.
