In Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (t…
What is the formula for similarity?
SSS or Side-Side-Side Similarity If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar. Thus, if AB/XY = BC/YZ = AC/XZ then ΔABC ~ΔXYZ.
How do you prove similarity in geometry?
2:3329:22Triangle Similarity - AA SSS SAS & AAA Postulates, Proving ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipNow another method that we could use to prove that the two triangles are similar is by calculatingMoreNow another method that we could use to prove that the two triangles are similar is by calculating the ratio of the corresponding sides. So if we can show that the ratio of a b and d e these two
What is similarity in geometry example?
For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other.
How do you solve similarity?
1:0511:40Similar Triangles - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo that's how you can set up the proportion. Now in order to solve it we need to cross multiply. SoMoreSo that's how you can set up the proportion. Now in order to solve it we need to cross multiply. So 8 times x that's 8x. And that's going to be equal to 6 times 12 which is 72..
What are the 3 ways to prove similarity?
These three theorems, known as Angle - Angle (AA), Side - Angle - Side (SAS), and Side - Side - Side (SSS), are foolproof methods for determining similarity in triangles.
What are the 3 similarity rules?
What are the triangle similarity criteria?AA. : Two pairs of corresponding angles are equal.SSS. : Three pairs of corresponding sides are proportional.SAS. : Two pairs of corresponding sides are proportional and the corresponding angles between them are equal.
What is a similar figure in geometry?
In terms of Maths, when two figures have the same shape but their sizes are different, then such figures are called similar figures.
How do you determine if triangles are similar?
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion . In other words, similar triangles are the same shape, but not necessarily the same size. The triangles are congruent if, in addition to this, their corresponding sides are of equal length.
What is a similarity statement in geometry?
Two polygons are similar if and only if corresponding angles are congruent and corresponding sides are proportional.
How do you solve congruence and similarity?
0:473:52Congruent and Similar Triangles - YouTubeYouTubeStart of suggested clipEnd of suggested clipBetween corresponding side lengths are the same. Or that all of the corresponding. Angles areMoreBetween corresponding side lengths are the same. Or that all of the corresponding. Angles are congruent to each other.
How do you find similarity and difference?
0:373:42Finding Difference Within Similarity - YouTubeYouTubeStart of suggested clipEnd of suggested clipMaking for a more interesting paper similarly. If you are analyzing two things that are obviouslyMoreMaking for a more interesting paper similarly. If you are analyzing two things that are obviously different finding a surprising similarity eight races new and interesting questions for you to pursue.
How do you prove two polygons are similar?
Two polygons are similar if their corresponding angles are congruent and the corresponding sides have a constant ratio (in other words, if they are proportional).
What is a similarity statement in geometry?
Two polygons are similar if and only if corresponding angles are congruent and corresponding sides are proportional.
What is the similarity theorem in geometry?
The fundamental theorem of similarity states that a line segment splits two sides of a triangle into proportional segments if and only if the segment is parallel to the triangle's third side.
How do you prove angle angles are similarity?
If all of the corresponding pairs of angles in two figures are congruent, then the figures are similar. If all of the corresponding pairs of sides in two figures have equal ratios, then the figures are similar.
How do you know if two objects are similar?
Two objects, shapes, or figures, are said to be similar when they have the exact same shape, but differ in size. In other words, we can obtain one object from the other by simply resizing the object. When two shapes are similar, they have the following properties relating their corresponding sides and angles.
How to tell if the angles are 90 degrees?
1) Since both shapes are rectangles, we know that all of the angles are 90 degrees, and thus the corresponding angles are equal. We need to verify that the ratios of the corresponding sides are equal. Comparing the shorter sides, we have 4.5 / 3 = 1.5. Comparing the longer sides, we have 7.5 / 5 = 1.5.
What do boxes look like?
All of the boxes are unassembled, so they look like cardboard rectangles. The boxes come in sizes extra small, small, medium, and large. As you are deciding which boxes to buy, you notice that all of the boxes have the exact same shape, but they differ in size.
What do moving boxes look like?
All of the boxes are unassembled, so they look like cardboard rectangles. The boxes come in sizes extra small, small, medium, and large.
What is the difference between a medium and a small box?
You notice that the lengths of the sides of the small box are indicated on the box, but the medium box only has the length of one side indicated.
How long is a ladder to paint the side of a house?
You have two ladders you can use to paint the side of your house. One is 10 feet long, and the other is 16 feet long. When you lean the 10-foot ladder up against the side of the house in the sturdiest way possible, you are able to measure that it reaches 8 feet up the side of the house.
When two shapes are similar, they have the same shape?
As we said, when two shapes are similar, they have the same shape, but differ in size. In other words, we can obtain one shape from the other by resizing one of the shapes. Because of this, similar shapes have two important properties that have to do with the measures of their angles and the lengths of their sides.
Why is similarity important in geometry?
The concept of similarity is fairly important in geometry and helps prove many theorems and corollaries. The ScienceStruck article provides an explanation of similarity statement in geometry with examples.
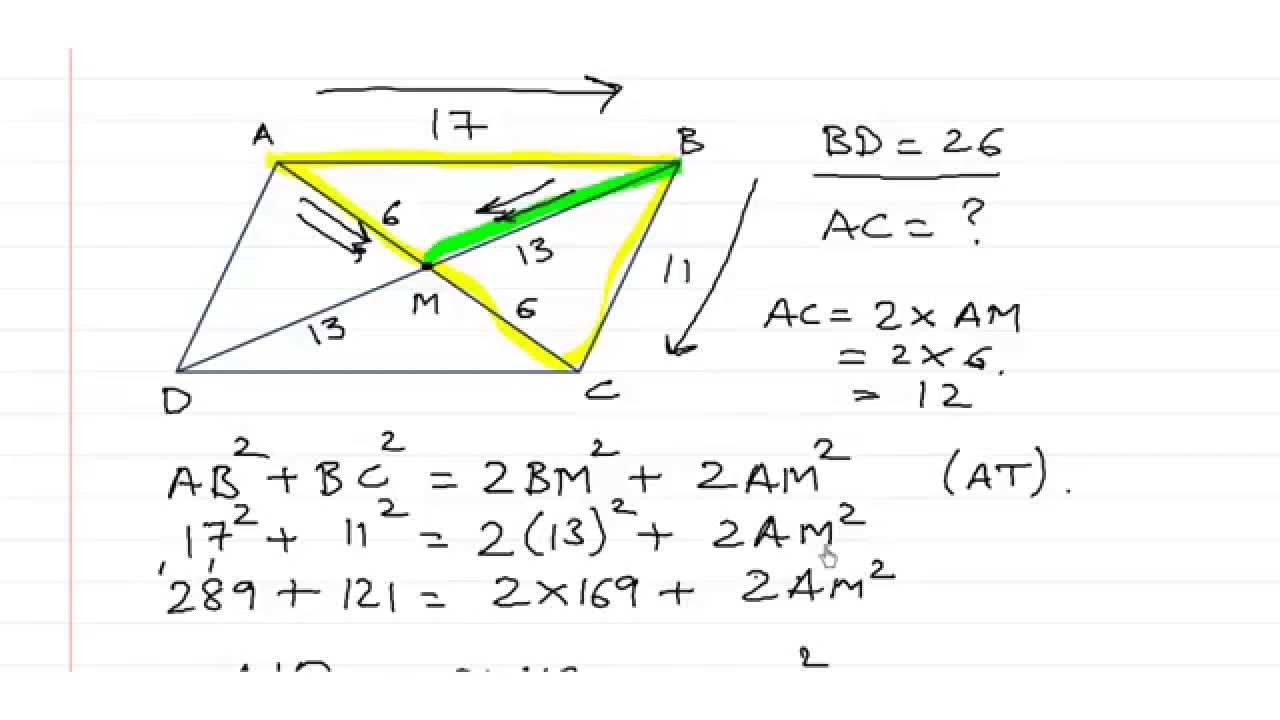
What is the theorem that all three triangles are similar to each other?
Theorem: If an altitude is drawn from the right angle of any right-angled triangle, then the two triangles so formed are similar to the original triangle, and all three triangles are similar to each other.
What is the statement of similarity?
The statement of similarity mentions that for two shapes to be similar, they must have the same angles and their sides must be in proportion. While writing a similarity statement in geometry, the reasons as to why the two shapes are similar, are explained. The concept is used to prove many theorems, as mentioned earlier.
What is the angle of BAC?
In the above figure, assume that angle BAC = 30° and angle ACB = 60°. Then, according to the theorem, angle ABD = 60° and angle DBC = 30°.
What is the ratio of two corresponding side lengths called?
In similar shapes, the sides are in proportion. This ratio of two corresponding side lengths is called scale factor. This must be mentioned while writing the similarity statement.
What is the ratio of the areas of a triangle?
In similar triangles, the ratio of their areas is equal to the square of the ratio of their sides.
Do congruent triangles have to be congruent?
Quick Tips to Remember. Two similar triangles need not be congru ent, but two congruent triangles are similar. If an acute angle of a right-angled triangle is congruent to an acute angle of another right-angled triangle, then the triangles are similar. All equilateral triangles are similar.
What is similarity in geometric shapes?
Geometric figures can be called similar figures if their shapes are the same regardless of size. Learn about geometric shapes, the definition of similar shapes, and how to test and compare for similarity. Updated: 11/09/2021
What does "similar shapes" mean?
We can define similar shapes as shapes that are the same with corresponding sides that are proportional in size. What does this mean? It sounds very technical, but it isn't. Why would you want to learn about similar shapes? Knowing how to work with similar shapes is a good skill to have not only for when you take math tests, but also in real life.
What is geometric shape?
Geometric shape. the form or shape of a particular object: two dimensional circles, triangles, squares, and rectangles. Similar shapes. shapes that are the same with corresponding sides that are proportional in size. Learning Outcomes. When this lesson ends, you should be ready to: Define what makes a geometric shape.
What does it mean to enroll in a course?
Enrolling in a course lets you earn progress by passing quizzes and exams.
When do geometric shapes have the same proportionality?
When we say geometric shape, we're talking about the form or shape of a particular object. Two shapes are similar when all corresponding sides have the same ratio of proportionality. This means that when you take the ratio of one pair of corresponding sides, this ratio must be the same as the ratios of the other corresponding sides of the shape. ...
What is the ratio of windows?
So, in your case, for the windows, your ratios are 2/16 for the shorter sides and 3/24 for the longer sides. We matched the sides with each other and made sure to write our ratios so that the first shape is always the top number. You can write your ratios any way you like, but you have to be consistent. If your second shape is on the top, then it must be on the top for all the other ratios.
How to write ratios?
To set up your ratios, you decide to write the smaller shape on top like you did last time. So matching the long sides together and the short sides together, you get ratios of 12/100 and 3/30. Now, let's simplify these ratios. 12/100 simplifies to 3/25 and 3/30 simplifies to 1/10.
How to tell if two figures are similar?
Two figures are similar if they have the same shape. Learn how to use ratios and proportions to solve similarity problems in a few simple steps.
When are two or more figures similar?
Two or more figures are similar if the corresponding angles are equal, and the corresponding sides are in proportion.
Who is Reza in math?
Reza. Reza is an experienced Math instructor and a test-prep expert who has been tutoring students since 2008. He has helped many students raise their standardized test scores--and attend the colleges of their dreams.
Can you add videos to your watch history?
Videos you watch may be added to the TV's watch history and influence TV recommendations. To avoid this, cancel and sign in to YouTube on your computer.
What Is The Difference Between Similarity And Congruency?
When two figures have the same shape and size, they are congruent. If the figures have the same shape, but not the same size, they are similar.
What is the SSS similarity criterion?
The SSS similarity criterion states that if the three sides of one triangle are respectively proportional to the three sides of another, then the two triangles are similar. This essentially means that any such pair of triangles will be equiangular (All corresponding angle pairs are equal) also.
What is the AA criterion for triangle similarity?
The AA criterion for triangle similarity states that if the three angles of one triangle are respectively equal to the three angles of the other, then the two triangles will be similar. In short, equiangular triangles are similar.
How to find the similarity of a triangle?
What Is The Application Of Similarity? 1 If two angles of two triangles are equal then their third angle is always equal. 2 The angle bisector of a triangle always divides the triangle into two similar triangles. (Angle Bisector Theorem) 3 If two similar triangles have sides in ratio x y x y then the ratio of their areas will be x2 y2 x 2 y 2
What is the angle bisector theorem?
The angle bisector of a triangle always divides the triangle into two similar triangles. (Angle Bisector Theorem) If two similar triangles have sides in ratio x y x y then the ratio of their areas will be x2 y2 x 2 y 2.
What is the difference between congruent and similar figures?
The major difference is all congruent figures are similar but similar figures are not congruent.
What does it mean when two linear figures are similar?
If two linear figures are similar it means that: All corresponding angle pairs are equal. All corresponding sides are proportional. However, due to its vast application, we will discuss the similarity of triangles. We use rules when we do not have information about all sides and all angles of two triangles.
