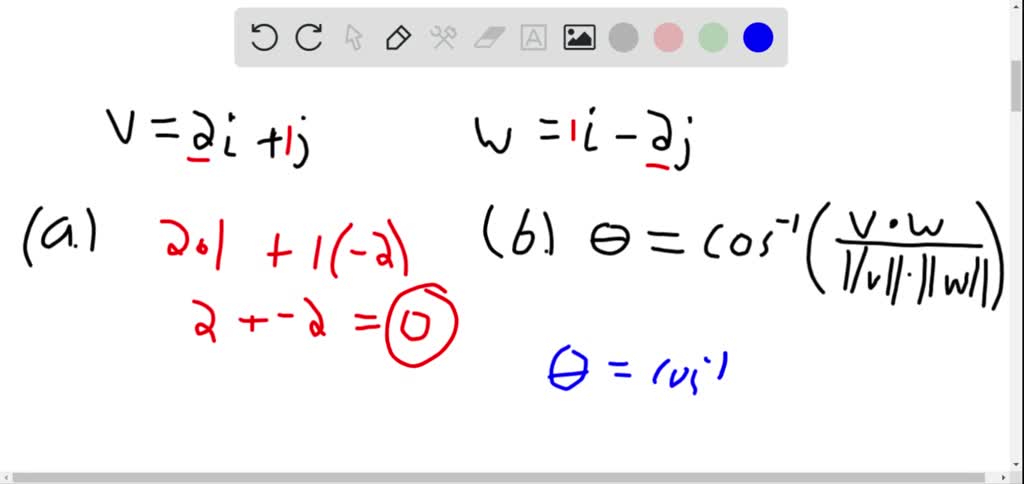
If u − = ⟨u1 u2⟩, and v − = ⟨v1 v2⟩, then the inner product (or dot product), a scaler quantity, is given by: u − ⋅ v − = u1v1 + u2v2 Inner Product = 0 ⇔ vectors are perpendicular
How to find the dot product of two vectors?
b n> we can find the dot product by multiplying the corresponding values in each vector and adding them together, or (a 1 * b 1) + (a 2 * b 2) + (a 3 * b 3) .... + (a n * b n). We can calculate the dot product for any number of vectors, however all vectors must contain an equal number of terms.
What is the use of dot product in math?
The dot product can be used to find out if two vectors are orthogonal (i.e they are perpendicular or their directions make 90 degrees). where θ is the angle between vectors u and v.
How do you find the product of two parallel vectors?
Compute the dot-product: The two vectors are not orthogonal; we know this, because orthogonal vectors have a dot-product that is equal to zero. Determine whether the two vectors are parallel by finding the angle between them. Compute the magnitude of both vectors: The angle between them is:
How do you determine whether u and V are orthogonal?
How do you determine whether u and v are orthogonal, parallel or neither given u = < 3, 15 > and v = < − 1, 5 >? Please see the explanation. Compute the dot-product: The two vectors are not orthogonal; we know this, because orthogonal vectors have a dot-product that is equal to zero.

How do you calculate the dot product of U and V?
0:031:03Dot Product of the Vectors u = (3, 6) and v = (-2, 4) - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo 6 times 4 so again you just multiply 3 times negative 2 so the first components. And then youMoreSo 6 times 4 so again you just multiply 3 times negative 2 so the first components. And then you multiply these second components so 6 times 4 3 times negative 2 is negative 6. And 6 times 4 is 24.
How do i find the dot product?
About Dot Products bn> we can find the dot product by multiplying the corresponding values in each vector and adding them together, or (a1 * b1) + (a2 * b2) + (a3 * b3) .... + (an * bn). We can calculate the dot product for any number of vectors, however all vectors must contain an equal number of terms.
How do you multiply v and u?
0:061:32Dot Product to Multiply Vectors - YouTubeYouTubeStart of suggested clipEnd of suggested clipY2 what you do is you multiply. The x coordinates together you multiply the Y coordinates together.MoreY2 what you do is you multiply. The x coordinates together you multiply the Y coordinates together.
What is the dot product of two orthogonal vectors U and V?
zeroThe dot product of two orthogonal vectors is zero.
What is the dot product of two vectors?
The dot product, or inner product, of two vectors, is the sum of the products of corresponding components. Equivalently, it is the product of their magnitudes, times the cosine of the angle between them. The dot product of a vector with itself is the square of its magnitude.
What is the dot product of i and j?
The dot product of two unit vectors is always equal to zero. Therefore, if i and j are two unit vectors along x and y axes respectively, then their dot product will be: i . j = 0.
How do u do UV?
0:062:15Finding the angle between two vectors u and v - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnswer there magnitude of v square root 3 squared plus 0 squared. So therefore i have cosine theta uMoreAnswer there magnitude of v square root 3 squared plus 0 squared. So therefore i have cosine theta u dot v is 6 divided by 3 times the square root of 5..
How do you find the angle between v and u?
So we can compute the angle θ between u and v using the dot product: θ = arccos ( u · v u v ) . u · v = u vcos(0) = u v > 0.
How do you multiply unit vectors?
2:009:57[Physics] Unit Vectors and Multiplying Vectors - YouTubeYouTubeStart of suggested clipEnd of suggested clipProduct as a b the magnitudes of a and b multiplied by cosine of theta where theta is the angle inMoreProduct as a b the magnitudes of a and b multiplied by cosine of theta where theta is the angle in between the two vectors. And so the scalar product can be a positive or negative scalar quantity.
What does it mean for U and V to be orthogonal?
Orthogonality. Two vectors u and v are said to be orthogonal. (perpendicular), if the angle between them is 90. ◦ .
What is the projection of U onto V?
The distance we travel in the direction of v, while traversing u is called the component of u with respect to v and is denoted compvu. The vector parallel to v, with magnitude compvu, in the direction of v is called the projection of u onto v and is denoted projvu.
How do you prove u and v are orthogonal?
1:474:211.3 Orthogonal Vectors - YouTubeYouTubeStart of suggested clipEnd of suggested clipOkay so if the vectors are orthogonal then the dot product is 0 and in fact that works in the otherMoreOkay so if the vectors are orthogonal then the dot product is 0 and in fact that works in the other direction if the dot product is 0 the vectors are orthogonal. So now we have a definition of
How do you find the dot product of two matrices?
Multiplication of two matrices involves dot products between rows of first matrix and columns of the second matrix. The first step is the dot product between the first row of A and the first column of B. The result of this dot product is the element of resulting matrix at position [0,0] (i.e. first row, first column).
How do you derive the dot product formula?
0:004:53Derivation of Dot Product Formula - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe the formula for u dot V naught as u dot V equals. The magnitude of U times the magnitude of VMoreThe the formula for u dot V naught as u dot V equals. The magnitude of U times the magnitude of V times the cosine of the angle between the two vectors.
What is the dot product of three vectors?
Scalar triple product is the dot product of a vector with the cross product of two other vectors, i.e., if a, b, c are three vectors, then their scalar triple product is a · (b × c). It is also commonly known as the triple scalar product, box product, and mixed product.
How do you find the dot product given the magnitude and angle?
0:373:15Given the magnitude and angle how do you find the dot product of two ...YouTubeStart of suggested clipEnd of suggested clipBetween two vectors we could find by using cosine of theta equals u dot v divided by the magnitudeMoreBetween two vectors we could find by using cosine of theta equals u dot v divided by the magnitude of u times the magnitude of v.
Calculator Use
Enter two or more vectors and click Calculate to find the dot product.
About Dot Products
In linear algebra, a dot product is the result of multiplying the individual numerical values in two or more vectors. If we defined vector a as <a 1, a 2, a 3 .... a n > and vector b as <b 1, b 2, b 3 ...
Further Reading
Khan, Salman "Vector dot product and vector length", The Khan Academy, Vector Dot Product and Vector Length .
Use of Dot Product Calculator
1 - Enter the components of the two vectors as real numbers in decimal form such as 2, 1.5, ... and press "Calculate the dot Product". The answer is a scalar. Characters other than numbers are not accepted by the calculator.
Applications of the Dot Product
The dot product has many applications in mathematics, physics, engineering, ... We will give some examples below.