How to Find the Equation of a Parabola?
- Take any parabola equation, and find a, b, c values from equation
- substitute those values in Vertex v(h, k).
- h = − b ( 2a), k = c − b2 ( 4a).
- focus of the x coordinate is − b ( 2a), and y coordinate is c − b2 − 1 ( 4a)
How do you find the focus of a parabola?
The focus of a parabola can be calculated by knowing the axis of the parabola, and the vertex of the parabola. For an equation of the parabola in standard form y 2 = 4ax, the vertex is the origin and the axis of this parabola is the x-axis.
How to find the equation of a parabola?
Finding the Equation of a Parabola Given Focus and Directrix. 1 Distance between the point on the parabola to the focus. 2 Distance between the point on the parabola to the directrix.
What is the equation of the parabola with focus (a) and directrix Y=C?
This equation in (x 0, y 0) is true for all other values on the parabola and hence we can rewrite with (x, y). Therefore, the equation of the parabola with focus (a, b) and directrix y = c is (x − a) 2 + b 2 − c 2 = 2 (b − c) y
How do you find the opening of a parabola?
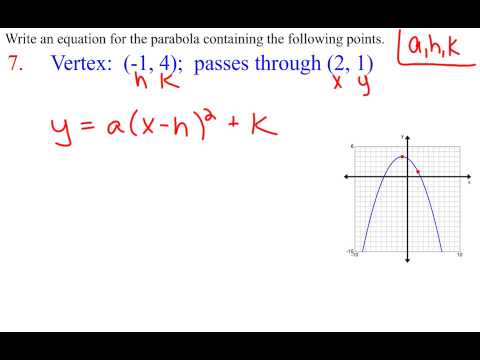
Remember, if the parabola opens vertically (which can mean the open side of the U faces up or down), you'll use this equation: y = a(x - h) 2 + k. And if the parabola opens horizontally (which can mean the open side of the U faces right or left), you'll use this equation:

What Is Focus of Parabola?
The focus of a parabola lies on the axis the parabola. The focus of the parabola helps in defining the parabola. A parabola represents the locus of a point which is equidistant from a fixed point called the focus and the fixed line called the directrix. The focus and the directrix are equidistant from the vertex of the parabola.
How to Locate Focus of Parabola?
The focus of a parabola lies on the axis of the parabola. The focus of a parabola lies at a distance of 'a' units from the vertex of the parabola. The vertex and the focus lies on the axes of the parabola and the axes can be calculated based on the equation of the parabola.
Examples on Focus of Parabola
Example 1: Find the equation of a parabola having the focus of (4, 0), the x-axis as the axis of the parabola, and the origin as the vertex of the parabola.
Practice Questions on Focus of Parabola
Here are a few activities for you to practice. Select your answer and click the "Check Answer" button to see the result.
FAQs on Focus of Parabola
The focus of a parabola can be calculated by knowing the axis of the parabola, and the vertex of the parabola. For an equation of the parabola in standard form y 2 = 4ax, the vertex is the origin and the axis of this parabola is the x-axis. Hence the focus of this parabola is (a, 0).
What is the point where the parabola opens?
In the graph above, you see a given line that intersects the directrix at a 90-degree angle. This straight line is called the axis of symmetry. The point that is marked C, signifying where the parabola opens, is called the vertex. The vertex is always midway between the focus and directrix of a parabola.
How to find the focus of a parabola?
In order to find the focus of a parabola, you must know that the equation of a parabola in a vertex form is y=a (x−h)2+k where a represents the slope of the equation. From the formula, we can see that the coordinates for the focus of the parabola is (h, k+1/4a).
What would happen if a parabola was rotated 90 degrees to the right?
If this parabola was rotated 90 degrees to the right, the fixed line representing the axis of symmetry would be situated along the x-axis. The equation of the parabola is now . The standard form of the equation of a parabola, where the conic shape of the parabola is formed along the y-axis, is .
What is a parabola in math?
A parabola is a curved figure where any point on the curve is equal distance from a fixed point (called the focus) and a fixed straight line (called the directrix). Let’s identify the parts of a parabolic function. In the graph above, you see a given line that intersects the directrix at a 90-degree angle. This straight line is called the axis of ...
Is the section on finding the focus of a parabola incorrect?
The Section on finding the focus of a parabola is incorrect.
Overview
- 1 What terms (like “parabola”) should I know?
2 Which equations/formulas do I use? - Co-authored by Christopher M. Osborne, PhD
Last Updated: October 2, 2022
Things You Should Know
- Depending on the type of parabola, use the equation
to determine the parabola’s vertex coordinates. - Once you have the vertex coordinates, use the formula
to calculate the graph coordinates of the focus.
Community Q&A
- Include your email address to get a message when this question is answered.
Tips
- All tip submissions are carefully reviewed before being published
You Might Also Like
- Calculate the Circumference of a Circle
Calculate the Diameter of a Circle - Find the Height of a Triangle
Calculate the Radius of a Circle
About This Article
- This article was co-authored by wikiHow staff writer, Christopher M. Osborne, PhD. Christopher …
Send fan mail to authors