Steps to Find Vertex Focus and Directrix Of The Parabola
- Step 1. Determine the horizontal or vertical axis of symmetry.
- Step 2. Write the standard equation.
- Step 3. Compare the given equation with the standard equation and find the value of a.
- Step 4. Find the focus, vertex and directrix using the equations given in the following table.
How to find the directrix of a parabola?
Equation of directrix is x = a. I.e x = 3 is the required equation for directrix. Vertex is (0,0). Length of latus rectum = 4a = 4×3 = 12. Example 2. Given the equation of a parabola 5y 2 = 16x, find the vertex, focus and directrix.
How do you find the focus and vertex of a parabola?
You can easily find the focus, vertex, and directrix from the standard form of a parabola. A parabola consists of three parts: Vertex, Focus, and Directrix. The vertex of a parabola is the maximum or minimum of the parabola and the focus of a parabola is a fixed point that lies inside the parabola.
How do you find the axis of a parabola?
Find the vertex, focus, the equation of directrix and length of the latus rectum of the parabola y 2 = -12x. Given equation of parabola is y 2 = -12x … (i) This equation has y 2 term. So the axis of the parabola is the x-axis. Focus is (-a,0) = (-3,0).
How do you draw a parabola using the equation (x-h) ^2?
After expressing the equation in the form (x - h)^2 = 4p (y - k), the vertex is given by (h, k), the focus is given by (h, k + p) and the directrix is given by the line y = k - p. After obtaining the vertex, the focus and the directrix, we can then sketch the parabola.
How do you find the vertex of a focus and Directrix?
The standard form is (x - h)2 = 4p (y - k), where the focus is (h, k + p) and the directrix is y = k - p. If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the x-axis, it has an equation of (y - k)2 = 4p (x - h), where the focus is (h + p, k) and the directrix is x = h - p.
How do you find the equation of a parabola given the Directrix and focus?
0:403:54Equation of Parabola Given Focus and Directrix - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd the vertex. And the focus we call that distance P. And the basic equation of a parabola is inMoreAnd the vertex. And the focus we call that distance P. And the basic equation of a parabola is in the form ax squared equals 4p Y or Y squared equals 4p.
How do you find the vertex of a parabola given the focus?
In order to find the focus of a parabola, you must know that the equation of a parabola in a vertex form is y=a(x−h)2+k where a represents the slope of the equation. From the formula, we can see that the coordinates for the focus of the parabola is (h, k+1/4a).
What is the formula for the vertex?
The vertex formula helps to find the vertex coordinates of a parabola. The standard form of a parabola is y = ax2 + bx + c. The vertex form of the parabola y = a(x - h)2 + k.
What is the relationship between Directrix and focus?
What are the focus and directrix of a parabola? Parabolas are commonly known as the graphs of quadratic functions. They can also be viewed as the set of all points whose distance from a certain point (the focus) is equal to their distance from a certain line (the directrix).
What's the vertex of the parabola?
The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry.
Is the vertex and focus the same?
The fixed-line is the directrix of the parabola and the fixed point is the focus denoted by F. The axis of the parabola is the line through the F and perpendicular to the directrix. The point where the parabola intersects the axis is called the vertex of the parabola.
How do you find the vertex in intercept form?
1:222:25How do you find the axis of symmetry and vertex in intercept form - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe had a table of values. What we did is we chose x values. And we plugged in that x value to findMoreWe had a table of values. What we did is we chose x values. And we plugged in that x value to find the y. Value. So i'm going to use function notation to find this so if i want to find the vertex.
What are the two ways to find the vertex?
0:395:20Learn two different ways to find the vertex and axis of symmetryYouTubeStart of suggested clipEnd of suggested clipRemember is x equals opposite of b divided. By 2a. So if you want to find the axis of symmetry. JustMoreRemember is x equals opposite of b divided. By 2a. So if you want to find the axis of symmetry. Just when given a parabola in this format just take opposite of b divided by 2a. So in this case to find
What are the equation of Directrices of parabola?
Equation of directrix is y = -a. i.e. y = -½ is the equation of directrix. Vertex of the parabola is (0,0).
How do you derive the equation of a parabola?
The general equation of a parabola is given by y = a(x – h)2 + k or x = a(y – k)2 +h. Here (h, k) denotes the vertex. y = a(x – h)2 + k is the regular form. x = a(y – k)2 +h is the sidewise form.
How do you find the equation of the Directrix is given?
2:203:42How to find the focus and directrix of a parabola - YouTubeYouTubeStart of suggested clipEnd of suggested clipLine so my y is going to equal k minus p. So now i just write in y equals and make sure you guysMoreLine so my y is going to equal k minus p. So now i just write in y equals and make sure you guys understand this one. Minus a negative one half right so therefore. My line is going to be y equals.
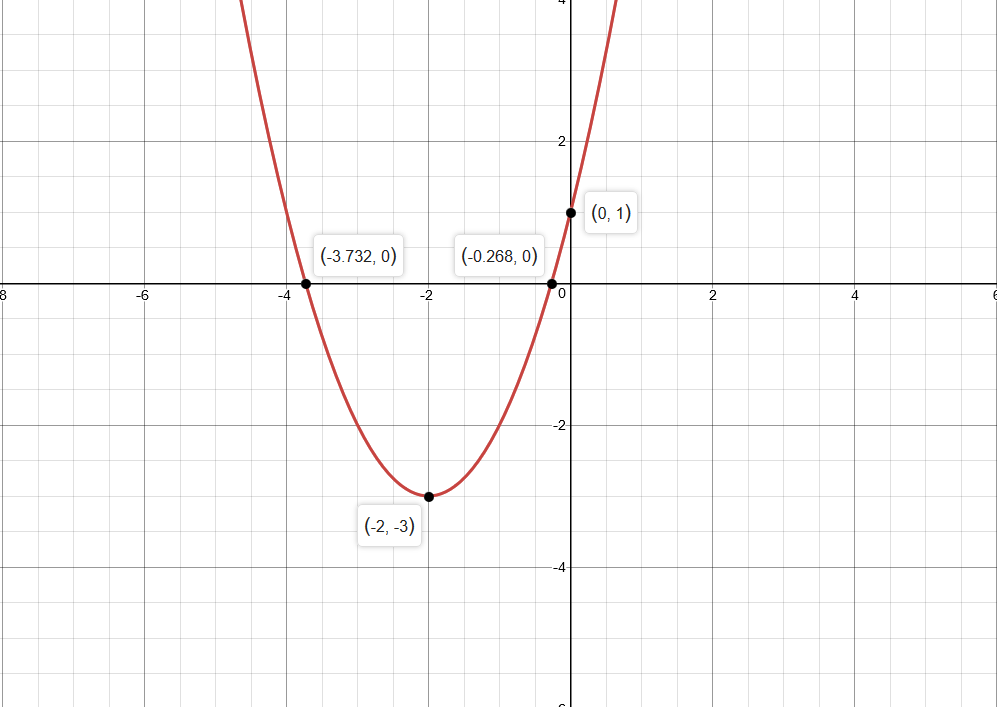
How to find the vertex of a parabola?
Steps to Find Vertex Focus and Directrix Of The Parabola. Step 1. Determine the horizontal or vertical axis of symmetry. Step 2. Write the standard equation. Step 3. Compare the given equation with the standard equation and find the value of a. Step 4. Find the focus, ver tex and directrix using the equations given in the following table .
What is the point where the parabola intersects the axis?
The point where the parabola intersects the axis is called the vertex of the parabola. In this article, we will learn how to find the vertex focus and directrix of the parabola with the given equation.
How is a parabola formed?
A parabola is a plane curve formed by a point moving so that its distance from a fixed point is equal to its distance from a fixed-line. The fixed-line is the directrix of the parabola and the fixed point is the focus denoted by F. The axis of the parabola is the line through the F and perpendicular to the directrix.
What is the equation of a parabola?
Given equation of parabola is y 2 = -12x … (i)
What is the required equation for directrix?
I.e x = 3 is the required equation for directrix.
What is the vertex of a parabola?
Vertex Form: The vertex form of a parabola is {eq}y = a (x-h)^2 + k {/eq}, where the point {eq} (h,k) {/eq} is the vertex of the parabola.
What is the Parabola made of?
Focus and Directrix: A parabola is made of the set of all points which are the same distance from a point called the focus, {eq}left (h, k + dfrac {1} {4a}right) {/eq}, and a line called the directrix, {eq}y = k - dfrac {1} {4a} {/eq}.
Who is Melissa from North Georgia?
Melissa is a former high school math teacher with 9 years of classroom experience in grades 9-12. She has a Bachelor's of Science in Math Education from North Georgia College and State University. She holds a professional teaching license in math grades 6-12, and is also gifted in-field certified.
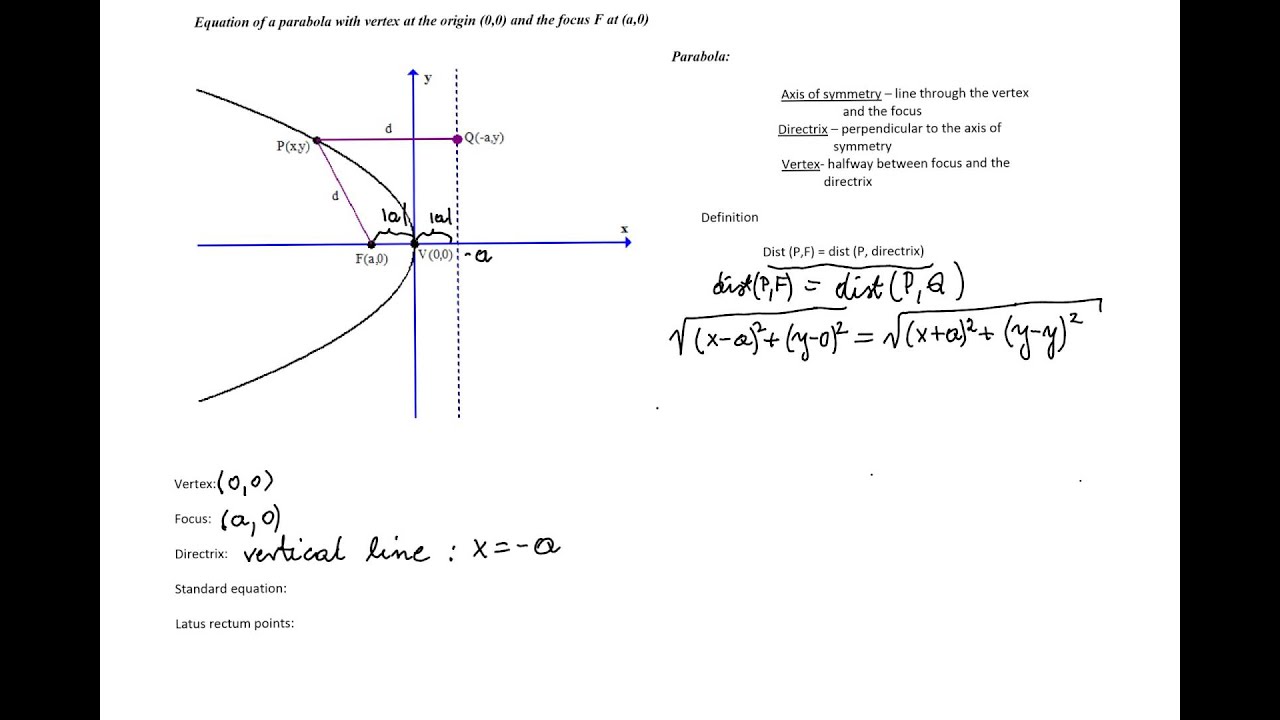
What Is Focus of Parabola?
The focus of a parabola lies on the axis the parabola. The focus of the parabola helps in defining the parabola. A parabola represents the locus of a point which is equidistant from a fixed point called the focus and the fixed line called the directrix. The focus and the directrix are equidistant from the vertex of the parabola.
How to Locate Focus of Parabola?
The focus of a parabola lies on the axis of the parabola. The focus of a parabola lies at a distance of 'a' units from the vertex of the parabola. The vertex and the focus lies on the axes of the parabola and the axes can be calculated based on the equation of the parabola.
Examples on Focus of Parabola
Example 1: Find the equation of a parabola having the focus of (4, 0), the x-axis as the axis of the parabola, and the origin as the vertex of the parabola.
Practice Questions on Focus of Parabola
Here are a few activities for you to practice. Select your answer and click the "Check Answer" button to see the result.
FAQs on Focus of Parabola
The focus of a parabola can be calculated by knowing the axis of the parabola, and the vertex of the parabola. For an equation of the parabola in standard form y 2 = 4ax, the vertex is the origin and the axis of this parabola is the x-axis. Hence the focus of this parabola is (a, 0).
