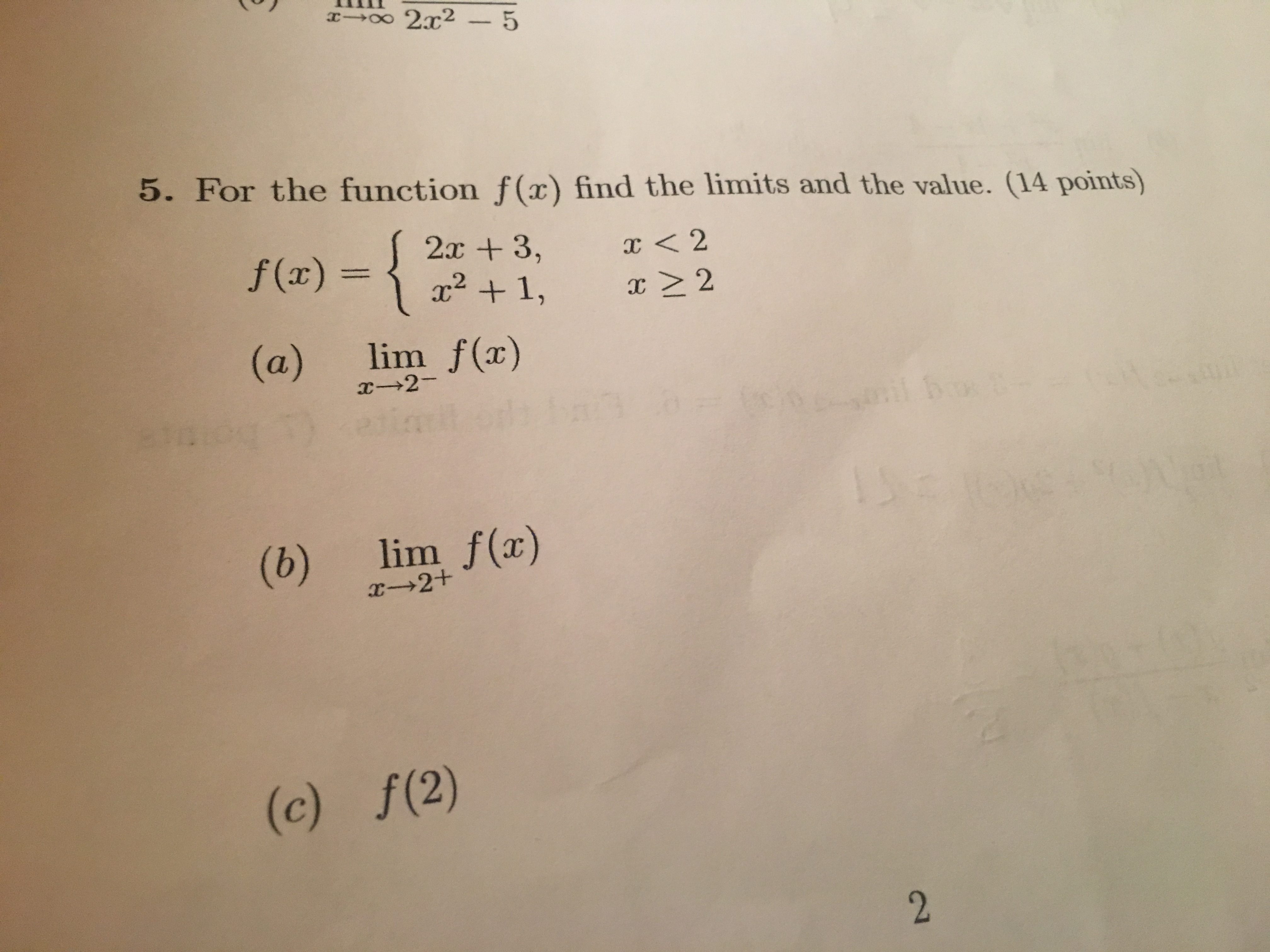Full Answer
What does f (x) = x2 mean?
What is a function?
What is a function in relation?
What is the most common name for a function?
What is the set of elements that get pointed to in Y?
How many parts are there in functions?
Is a set of coordinates a function?
See 4 more
About this website

What is a Function? Definition, Types and Notation - BYJUS
Learn what is a function along with its types and examples. A function in Maths is defined as a relation between two or more variables, whose graph can be plotted in cartesian plane.
Algebra - The Definition of a Function - Lamar University
In this section we will formally define relations and functions. We also give a “working definition” of a function to help understand just what a function is. We introduce function notation and work several examples illustrating how it works. We also define the domain and range of a function. In addition, we introduce piecewise functions in this section.
Function Definition & Meaning - Merriam-Webster
The meaning of FUNCTION is professional or official position : occupation. How to use function in a sentence. Synonym Discussion of Function.
What does f (x) = x2 mean?
f (x) = x2 shows us that function " f " takes " x " and squares it.
What is a function?
A function relates an input to an output.
What is a function in relation?
a function takes elements from a set (the domain) and relates them to elements in a set (the codomain ). all the outputs (the actual values related to) are together called the range. a function is a special type of relation where: every element in the domain is included, and.
What is the most common name for a function?
Names. First, it is useful to give a function a name. The most common name is " f ", but we can have other names like " g " ... or even " marmalade " if we want. what goes into the function is put inside parentheses () after the name of the function:
What is the set of elements that get pointed to in Y?
the set of elements that get pointed to in Y (the actual values produced by the function) is called the Range . We have a special page on Domain, Range and Codomain if you want to know more.
How many parts are there in functions?
We will see many ways to think about functions, but there are always three main parts:
Is a set of coordinates a function?
So a set of coordinates is also a function (if they follow the rules above, that is)
What is the domain of f?
Domain of f = {1, 4, 9, 16} = A.
Is the above relation a function?
So, the above relation is not a function.
What does f (x) mean?
Suppose y = f (x) is a function. What does it mean? f (x) represents a function i.e. an expression in terms of x which equals to y. That is, y is expressed in terms of x or y is dependent on x. Likewise, we can arrange the above equation so that x becomes dependent on y, and y becomes independent.
What is a function like?
Functions are like machine, one specific input gives you one specific output.
What happens when you put a value of x in a function?
when you put a value of x (set of domains) in a function you get y (set of ranges). In an “inverse function” the opposite happens. Meaning, when you put a value of y you will get x.f^-1 (x) is the inverse function of f (x).
What is the inverse of a function?
The inverse of a function “undoes” what a function “does”. Another way you could look at it is that the input of a function is the output of its inverse function, and the output of a function is the input of its inverse function. An example of a function and it’s inverse could be: F (x) = 5x + 3. F^-1 (x) = (x - 3) / 5.
How to find the symmetry of reflection?
If you plot f (x) = x^3 and g (x) = x^ (1/3) you will see the symmetry of the reflection. Also note for this f and its inverse g, f (g (x)) = x, and g (f (x)) = x.
Can you replace f (x) with x?
You can also replace f (x) by the same variable x.
Is inverse function the same as reciprocal function?
P.S. - Inverse functions are not to be confused with reciprocal functions, they both are not the same. Reciprocal functions are (f (x))^-1, whereas inverse functions are f^-1 (x) ( very critical)
Why isn't function #1 a 1 to 1?
Function #1 is not a 1 to 1 because the range element of '5' goes with two different elements ( 4 and 11) in the domain. .
What test is used to determine whether a function is one to one?
We can also look at the graphs of functions and use the horizontal line test to determine whether or not a function is one to one.
What happens if an element repeats in a function?
If an element in the range repeats, like 14 in function #2 , then you do not have a 1 to 1 function.
Why is #1 not one to one?
In a one to one function, every element in the range corresponds with one and only one element in the domain. So, #1 is not one to one because the range element. 5 goes with 2 different values in the domain (4 and 11). Diagram 1.
Is a parabola one to one?
As the picture below shows, parabolas are not one to one.
Is "no" a one to one function?
Since the answer is 'no', this is a one-to-one function.
Is x = 2 a function?
Vertical lines such as x = 2 are not functions at all.
How to tell if a function is 1 to 1?
If the graph of a function f is known, it is easy to determine if the function is 1 -to- 1 . Use the Horizontal Line Test. If no horizontal line intersects the graph of the function f in more than one point, then the function is 1 -to- 1 .
What is the function of f?
A function f is 1 -to- 1 if no two elements in the domain of f correspond to the same element in the range of f . In other words, each x in the domain has exactly one image in the range. And, no y in the range is the image of more than one x in the domain.
What does f (x) = x2 mean?
f (x) = x2 shows us that function " f " takes " x " and squares it.
What is a function?
A function relates an input to an output.
What is a function in relation?
a function takes elements from a set (the domain) and relates them to elements in a set (the codomain ). all the outputs (the actual values related to) are together called the range. a function is a special type of relation where: every element in the domain is included, and.
What is the most common name for a function?
Names. First, it is useful to give a function a name. The most common name is " f ", but we can have other names like " g " ... or even " marmalade " if we want. what goes into the function is put inside parentheses () after the name of the function:
What is the set of elements that get pointed to in Y?
the set of elements that get pointed to in Y (the actual values produced by the function) is called the Range . We have a special page on Domain, Range and Codomain if you want to know more.
How many parts are there in functions?
We will see many ways to think about functions, but there are always three main parts:
Is a set of coordinates a function?
So a set of coordinates is also a function (if they follow the rules above, that is)