how do you prove a quadrilateral

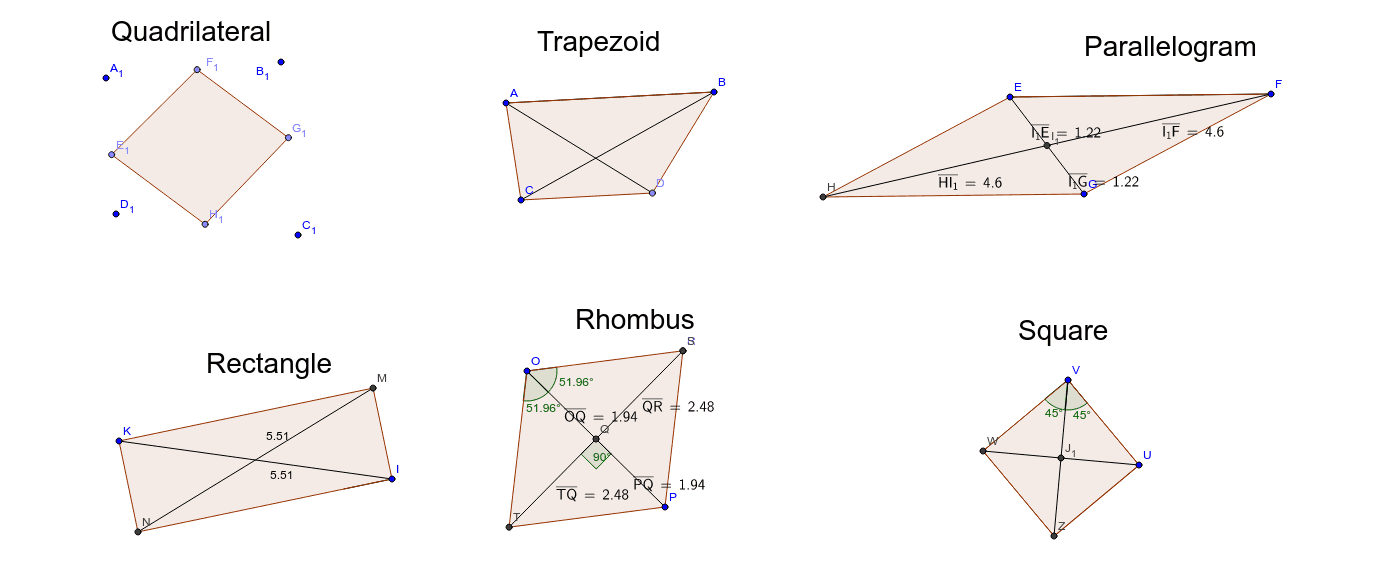
Here are the six ways to prove a quadrilateral is a parallelogram:

• Prove that opposite sides are congruent.
• Prove that opposite angles are congruent.
• Prove that opposite sides are parallel.
• Prove that consecutive angles are supplementary (adding to 180°)
• Prove that an angle is supplementary to both its consecutive angles.
• Prove that the quadrilateral's diagonals bisect each other.

Full Answer

How do you prove a quadrilateral is congruent?

Criteria proving a quadrilateral is parallelogram. 1) If a quadrilateral has one pair of sides that are both parallel and congruent. 2) If all opposite sides of the quadrilateral are congruent. 3) Both pairs of opposite sides are parallel. 4) Opposite angles are congruent. 5) Diagonals bisect.

How do you prove that the opposite sides of a quadrilateral are parallel?

Here, for example, you are given a quadrilateral and told that its opposite sides are congruent. Theorem: If a transversal cuts across two lines and the alternate interior angles are congruent, then the lines are parallel The two-column proof proved the quadrilateral is a parallelogram by proving opposite sides were parallel.

What is the proof of the cyclic quadrilateral?

There are two important theorems which prove the cyclic quadrilateral. In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary. Proof: Let us now try to prove this theorem.

What are the 5 criteria to prove a quadrilateral is a parallelogram?

If a quadrilateral meets any of the 5 criteria below, then it must be a parallelogram. Criteria proving a quadrilateral is parallelogram 1) If a quadrilateral has one pair of sides that are both parallel and congruent. 2) If all opposite sides of the quadrilateral are congruent.

How do you prove a quadrilateral is a quadrilateral?

Here are the six ways to prove a quadrilateral is a parallelogram:Prove that opposite sides are congruent.Prove that opposite angles are congruent.Prove that opposite sides are parallel.Prove that consecutive angles are supplementary (adding to 180°)Prove that an angle is supplementary to both its consecutive angles.More items...

What are quadrilateral proofs?

1) Opposite angles in a quadrilateral are congruent. 2) Parallel lines have congruent corresponding angles. 3) Corresponding parts of congruent triangles are congruent. 4) Alternate interior angles in congruent triangles are congruent.

How do you prove ABCD is a quadrilateral?

e.g. ABCD is a quadrilateral which has four sides AB, BC, CD and DA, four angles ∠A,∠B,∠C and ∠D and four vertices A, B, C and D and also has two diagonals AC and BD. i.e. A quadrilateral has four sides, four angles, four vertices and two diagonals. Hence, ∠A + ∠B + ∠C + ∠D = 360o Proved.

How do you know if it's quadrilateral?

A quadrilateral is a polygon that has exactly four sides. (This also means that a quadrilateral has exactly four vertices, and exactly four angles.)

What formula do you use to prove a quadrilateral is a parallelogram?

If — AB ≅ — CD and — BC ≅ — DA , then ABCD is a parallelogram. If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

How do you prove quadrilaterals congruent?

Generally we have to put side's interior angles of one quadrilateral in correspondence with sides and angles of another and to prove that all correspondence with sides and angles of another and to prove that all corresponding pairs of sides and angles are congruent.

How do you prove a parallelogram?

Well, we must show one of the six basic properties of parallelograms to be true!Both pairs of opposite sides are parallel.Both pairs of opposite sides are congruent.Both pairs of opposite angles are congruent.Diagonals bisect each other.One angle is supplementary to both consecutive angles (same-side interior)More items...•

Which statement about Quadrilaterals is true?

3:206:21Determine True Statements About Quadrilaterals (Common Core 5/6 ...YouTubeStart of suggested clipEnd of suggested clipAnd all four sides have the same length.MoreAnd all four sides have the same length.

Is quadrilateral ABCD a square?

Quadrilateral ABCD is a square. Explanation: Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle.

How do you explain quadrilaterals?

Properties of QuadrilateralsThey have four vertices.They have four sides.The sum of all interior angles is 360°.They have two diagonals.A quadrilateral can be regular or irregular. A regular quadrilateral must have 4 equal sides, and 4 equal angles, and its diagonals must bisect each other.

How do you prove two sides of a quadrilateral are parallel?

14:5221:30Proving a Quadrilateral a Parallelogram | Geometry Proof ...YouTubeStart of suggested clipEnd of suggested clipHere we have two more theorems in this video geometry lesson that we're not necessarily going toMoreHere we have two more theorems in this video geometry lesson that we're not necessarily going to prove in the video these will be left for my students to complete as exercises and/or outside of class.

What are the properties of quadrilateral?

Every quadrilateral has 4 vertices, 4 angles, and 4 sides. The total of its interior angles = 360 degrees....Properties of KiteThe pair of adjacent sides of a kite are of the same length.The largest diagonal of a kite bisect the smallest diagonal.Only one pair of opposite angles are of the same measure.

How do you prove that a quadrilateral is a square?

If a quadrilateral has four congruent sides and four right angles, then it's a square (reverse of the square definition). If two consecutive sides of a rectangle are congruent, then it's a square (neither the reverse of the definition nor the converse of a property).

How do you prove that a quadrilateral is a rectangle?

There are a few ways to prove a quadrilateral is a rectangle. Here are three of the easiest ways: 1) Show all angles are 90°; 2) Show that one pair of sides is parallel and that two opposite angles are 90°; 3) Show the diagonals bisect each other and are of equal length.

What are triangle proofs?

If two triangles have a pair of congruent angles, then we know their opposite side of that angle must be in proportion to each other. If we also have two pairs of sides that are of the same proportions then these triangles would be similar. This theorem guarantees these conditions are met.

How do you prove that a quadrilateral is a rhombus?

To prove a quadrilateral is a rhombus, here are three approaches: 1) Show that the shape is a parallelogram with equal length sides; 2) Show that the shape's diagonals are each others' perpendicular bisectors; or 3) Show that the shape's diagonals bisect both pairs of opposite angles.

How many ways can we prove a quadrilateral is a parallelogram?

We can use these features and properties to establish six ways of proving a quadrilateral is a parallelogram.

What is a quadrilateral?

Quadrilaterals are four-sided, closed polygons. Their sides can be of any length, their angles either congruent or not. The term "quadrilateral" is the loosest possible classification of a four-sided polygon.

How many right angles does a quadrilateral have?

If the quadrilateral has one right angle, then it has four right angles. Bisecting diagonals. Each diagonal separates the parallelogram into two congruent triangles. Parallelograms get their names from having two pairs of parallel opposite sides.

Why are fish angles congruent?

They are congruent because they are vertical angles ( opposite angles sharing a vertex point).

What are the properties of a parallelogram?

Parallelograms are special types of quadrilaterals with opposite sides parallel. Parallelograms have these identifying properties: 1 Congruent opposite sides 2 Congruent opposite angles 3 Supplementary consecutive angles 4 If the quadrilateral has one right angle, then it has four right angles 5 Bisecting diagonals 6 Each diagonal separates the parallelogram into two congruent triangles

How to prove that opposite angles are congruent?

Prove that opposite angles are congruent. Prove that opposite sides are parallel. Prove that consecutive angles are supplementary (adding to 180°) Prove that an angle is supplementary to both its consecutive angles. Prove that the quadrilateral's diagonals bisect each other.

What are the sides of a congruent triangle?

Those two angles are alternate interior angles, and if they are congruent, then sides FI and SH are parallel. You can repeat the steps to prove FH and IS parallel, which means two pairs of opposite sides are parallel.

Criteria needed to prove a shape is a parallogram

There are 5 distinct ways to know that a quadrilateral is a paralleogram. If a quadrilateral meets any of the 5 criteria below, then it must be a parallelogram.

Criteria proving a quadrilateral is parallelogram

1) If a quadrilateral has one pair of sides that are both parallel and congruent.

What is the quadrilateral if its diagonals bisect each other?

Theorem 3: A quadrilateral is a parallelogram if its diagonals bisect each other.

What type of quadrilaterals are parallelograms?

This lesson investigates a specific type of quadrilaterals: the parallelograms. These are defined by specific features that other four-sided polygons may miss. In parallelograms opposite sides are parallel and congruent, opposite angles are congruent, adjacent angles are supplementary, and the diagonals bisect each other.

Do parallelograms have all four characteristics?

Although all parallelograms should have these four characteristics, one does not need to check all of them in order to prove that a quadrilateral is a parallelogram. The next section shows how, often, some characteristics come as a consequence of other ones, making it easier to analyze the polygons.

Is a parallelogram a quadrilateral?

No. Every parallelogram is a quadrilateral, but a quadrilateral is only a parallelogram if it has specific characteristics, such as opposite sides are parallel and congruent, opposite angles are congruent, adjacent angles are supplementary, and the diagonals bisecting each other.

What is a quadrilateral?

A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point.

What happens when the perpendicular bisectors of a quadrilateral meet?

If it is a cyclic quadrilateral, then the perpendicular bisectors will be concurrent compulsorily. In a cyclic quadrilateral, the four perpendicular bisectors of the given four sides meet at the centre O.

What is the ratio between diagonals and sides?

The ratio between the diagonals and the sides can be defined and is known as Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.

What is a quadrilateral that is circumscribed in a circle called?

The definition states that a quadrilateral which is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of quadrilateral lie in the circumference of the circle. Let us understand with a diagram.

How to find the sum of the angles formed at the vertices of a cyclic quadri?

Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360 o and the sum of angles formed at the opposite vertices is always supplementary.

What is the name of the circle that has all the vertices of a polygon on its circumference?

The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle. A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’.

What is the exterior angle of a cyclic quadrilateral?

The exterior angle formed if any one side of the cyclic quadrilateral produced is equal to the interior angle opposite to it. In a given cyclic quadrilateral, d1 / d2 = sum of the product of opposite sides, which shares the diagonals endpoints.

What is a quadrilateral inscribed in a circle?

A quadrilateral inscribed in a circle is known as a cyclic quadrilateral. It is a particular type of quadrilateral whose four vertices lie on the circumference of a circle. In a cyclic quadrilateral, the four sides of the quadrilateral are the chords of the circle. This article will discuss in detail the cyclic quadrilateral, its definition, ...

What is the exterior angle of a quadrilateral?

An exterior angle of a quadrilateral is an angle formed by one of its sides and the extension of an adjacent side. Let the side of the cyclic quadrilateral is extended to. Here and are linear pair, their sum is and the angles and are the opposite angles of a cyclic quadrilateral, and their sum is also.

What is supplementary in a cyclic quadrilateral?

1. In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.

What is a cyclic quadrilateral?

It is a particular type of quadrilateral whose four vertices lie on the circumference of a circle. In a cyclic quadrilateral, the four sides of the quadrilateral are the chords of the circle.

What is the sum of the opposite angles of a quadrilateral?

2. If opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.

What is the proof given?

Proof: Given: is a cyclic quadrilateral of a circle with a centre at . To prove: is the chord of the circle. (Angles in the same segment are equal) is the chord of the circle. (Angles in the same segment are equal) is the chord of the circle. (Angles in the same segment are equal) is the chord of the circle.

How many theorems are related to the cyclic quadrilateral?

There are three important theorems related to the cyclic quadrilateral.