Note - To rotate a point (a, b) in cartesian co-ordinate by angle ϕ you just need to multiply matrix [ cos ϕ − sin ϕ sin ϕ cos ϕ] and [ a b], hence you can apply this matrix multiplication to [ a − c b − d] and then add c and d to the x and y co-ordinate. Share edited Aug 20, 2016 at 3:50
How to rotate objects on the coordinate plane?
- Draw a ray from the center of rotation to the point you wish to rotate.
- Draw an angle with the center of rotation as the vertex.
- Use a compass to draw a circle (arc) with the center at the center of rotation and a radius from the center of rotation to the point you are rotating.
- Now rotate all the other points and connect the dots.
What are the different parts of a Cartesian coordinate system?
Important Terms:
- Quadrants: Moreover, the axes divide the plane into four parts and these four parts are called quadrants (one-fourth part).
- Cartesian Plane: A plane consists of axes and quadrants. Thus, we call the plane the Cartesian Plane, or the Coordinate Plane, or the x-y plane.
- Number line: A line with a chosen Cartesian system is called a number line. ...
How do you read Cartesian coordinates?
How do you read Cartesian coordinates? The position of any point on the Cartesian plane is described by using two numbers: (x, y). The first number, x, is the horizontal position of the point from the origin. It is called the x-coordinate. The second number, y, is the vertical position of the point from the origin. What is Cartesian thinking?
How to graph points using Cartesian coordinates?
Cartesian Coordinates. Using Cartesian Coordinates we mark a point on a graph by how far along and how far up it is: The point (12,5) is 12 units along, and 5 units up. They are also called Rectangular Coordinates because it is like we are forming a rectangle.

How do you rotate Cartesian coordinates?
The rule of a rotation rO of 90° centered on the origin point O of the Cartesian plane, in the positive direction (counter-clockwise), is rO:(x,y)↦(−y,x). The rule of a rotation rO of 180° centered on the origin point O of the Cartesian plane, in the positive direction (counter-clockwise) is rO:(x,y)↦(−x,−y).
How do you rotate coordinates on a graph?
0:001:32Rotations (Easier Method) 90 180 270 - YouTubeYouTubeStart of suggested clipEnd of suggested clipPosition. Ok and now what you want to do is plot these points on the diagram. So negative 1 0 isMorePosition. Ok and now what you want to do is plot these points on the diagram. So negative 1 0 is going to be here.
What is the rule for rotating coordinates?
Here are the rotation rules: 90° clockwise rotation: (x,y) becomes (y,-x) 90° counterclockwise rotation: (x,y) becomes (-y,x) 180° clockwise and counterclockwise rotation: (x, y) becomes (-x,-y)
How do you rotate a line on a coordinate plane?
6:5210:36How to Rotate Objects on the Coordinate Plane - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo each time you sweep through a whole quadrant of the coordinate plane you're going 90 degrees. SoMoreSo each time you sweep through a whole quadrant of the coordinate plane you're going 90 degrees. So we want to do 180. It's it's a positive rotation. So we're doing we're going counterclockwise.
How do you rotate a Cartesian plane 90 degrees?
The rule for a rotation by 90° about the origin is (x,y)→(−y,x) .
How do you rotate an equation?
To rotate any curve by any angle, you need to use parametric equations. x=tcosθ−f(t)sinθ, y=tsinθ+f(t)cosθ.
How do you rotate?
When this accessibility setting is on, the screen automatically rotates when you move your device between portrait and landscape position....How to automatically rotate your screenOpen your device's Settings app. .Select Accessibility.Select Auto-rotate screen.
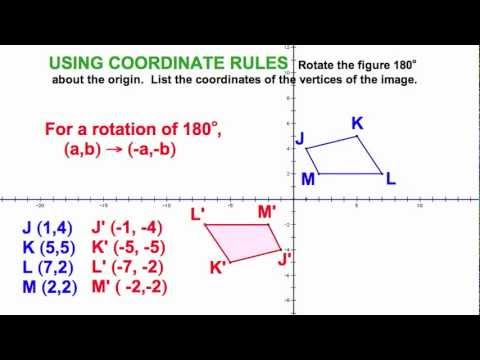
How do you rotate coordinates 180 degrees?
180 Degree Rotation When rotating a point 180 degrees counterclockwise about the origin our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.
How do you rotate a point 90 degrees clockwise?
Answer: To rotate the figure 90 degrees clockwise about a point, every point(x,y) will rotate to (y, -x). Let's understand the rotation of 90 degrees clockwise about a point visually. So, each point has to be rotated and new coordinates have to be found. Then we can join the points and find the new positioned figure.
What happens to coordinates when rotated 270 degrees clockwise?
Rotating a figure 270 degrees clockwise is the same as rotating a figure 90 degrees counterclockwise. Example: What will be the coordinate of a point having coordinates (3,-6) after rotations as 90° anti-clockwise and 270° clockwise? The coordinate of a point is (-6, -3).
How do you rotate coordinate 45 degrees?
If we represent the point (x,y) by the complex number x+iy, then we can rotate it 45 degrees clockwise simply by multiplying by the complex number (1−i)/√2 and then reading off their x and y coordinates. (x+iy)(1−i)/√2=((x+y)+i(y−x))/√2=x+y√2+iy−x√2. Therefore, the rotated coordinates of (x,y) are (x+y√2,y−x√2).
How do you rotate the shape of a degree?
Then draw in the shape below. Here is another example. Rotate the shape 270° clockwise about the point using tracing paper....Rules for Rotating a Shape About the Origin.Clockwise rotation angleCounter-clockwise rotation angleRule90°270°(x, y) → (y, -x)180°180°(x, y) → (-x, -y)1 more row•Sep 28, 2021
How do you rotate a shape 90 degrees around a point?
2:438:39Rotation around a point - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd y. Change the sign of my X swap my x and y change the sign of my X swap. My x and y change theMoreAnd y. Change the sign of my X swap my x and y change the sign of my X swap. My x and y change the sign of my X. Okay. Now because we subtracted this point from here to get these pretend.
How do you rotate a triangle 90 degrees about the origin?
0:574:48Learn how to rotate a triangle 90 degrees clockwise about the originYouTubeStart of suggested clipEnd of suggested clipSo when it says rotate clock 90 degrees clockwise all i'm going to do is take this piece of paper.MoreSo when it says rotate clock 90 degrees clockwise all i'm going to do is take this piece of paper. And rotate it 90 degrees. Right so now where this was my x-axis. Now rotating on degrees now that's
How do you rotate coordinates 180 degrees?
180 Degree Rotation When rotating a point 180 degrees counterclockwise about the origin our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.
How do you rotate coordinate 45 degrees?
If we represent the point (x,y) by the complex number x+iy, then we can rotate it 45 degrees clockwise simply by multiplying by the complex number (1−i)/√2 and then reading off their x and y coordinates. (x+iy)(1−i)/√2=((x+y)+i(y−x))/√2=x+y√2+iy−x√2. Therefore, the rotated coordinates of (x,y) are (x+y√2,y−x√2).
How do you rotate a point 90 degrees clockwise?
Answer: To rotate the figure 90 degrees clockwise about a point, every point(x,y) will rotate to (y, -x). Let's understand the rotation of 90 degrees clockwise about a point visually. So, each point has to be rotated and new coordinates have to be found. Then we can join the points and find the new positioned figure.
How do you rotate a point on a graph 180 degrees?
0:132:36Rotate 180 Degrees Around The Origin - YouTubeYouTubeStart of suggested clipEnd of suggested clipNotice that all of our values are positive because they are located in quadrant number one to rotateMoreNotice that all of our values are positive because they are located in quadrant number one to rotate any object 180 degrees around the origin. Simply change all of the signs inside your parenthesis.
How to get a Cartesian coordinate?
In that case, each coordinate is obtained by projecting the point onto one axis along a direction that is parallel to the other axis (or, in general, to the hyperplane defined by all the other axes). In such an oblique coordinate system the computations of distances and angles must be modified from that in standard Cartesian systems, and many standard formulas (such as the Pythagorean formula for the distance) do not hold (see affine plane ).
What is Cartesian coordinate system?
A Cartesian coordinate system ( UK: / kɑːˈtiːzjən /, US: / kɑːrˈtiʒən /) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis (plural axes) of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.
What are the first and second coordinates of a coordinate system called?
The first and second coordinates are called the abscissa and the ordinate of P, respectively; and the point where the axes meet is called the origin of the coordinate system. The coordinates are usually written as two numbers in parentheses, in that order, separated by a comma, as in (3, −10.5).
How many octants are there in a three-dimensional Cartesian system?
Similarly, a three-dimensional Cartesian system defines a division of space into eight regions or octants, according to the signs of the coordinates of the points. The convention used for naming a specific octant is to list its signs; for example, (+ + +) or (− + −). The generalization of the quadrant and octant to an arbitrary number of dimensions is the orthant, and a similar naming system applies.
What are the letters that represent the coordinates of a point?
The origin is often labelled with the capital letter O. In analytic geometry, unknown or generic coordinates are often denoted by the letters ( x, y) in the plane, and ( x, y, z) in three-dimensional space. This custom comes from a convention of algebra, which uses letters near the end of the alphabet for unknown values (such as the coordinates of points in many geometric problems), and letters near the beginning for given quantities.
What is the first coordinate of a two-dimensional cartesian system?
In mathematical illustrations of two-dimensional Cartesian systems, the first coordinate (traditionally called the abscissa) is measured along a horizontal axis, oriented from left to right. The second coordinate (the ordinate) is then measured along a vertical axis, usually oriented from bottom to top. Young children learning the Cartesian system, commonly learn the order to read the values before cementing the x -, y -, and z -axis concepts, by starting with 2D mnemonics (for example, 'Walk along the hall then up the stairs' akin to straight across the x -axis then up vertically along the y -axis).
What is a coordinate system in two dimensions?
A Cartesian coordinate system in two dimensions (also called a rectangular coordinate system or an orthogonal coordinate system) is defined by an ordered pair of perpendicular lines (axes), a single unit of length for both axes, and an orientation for each axis.
How to rotate axes in two dimensions?
In mathematics, a rotation of axes in two dimensions is a mapping from an xy - Cartesian coordinate system to an x'y' -Cartesian coordinate system in which the origin is kept fixed and the x' and y' axes are obtained by rotating the x and y axes counterclockwise through an angle#N#θ {displaystyle [&theta &] }#N#. A point P has coordinates ( x, y) with respect to the original system and coordinates ( x', y') with respect to the new system. In the new coordinate system, the point P will appear to have been rotated in the opposite direction, that is, clockwise through the angle#N#θ {displaystyle theta }#N#. A rotation of axes in more than two dimensions is defined similarly. A rotation of axes is a linear map and a rigid transformation .
Where are the foci located in coordinate geometry?
For example, to study the equations of ellipses and hyperbolas, the foci are usually located on one of the axes and are situated symmetrically with respect to the origin.
Overview
Cartesian formulae for the plane
The Euclidean distance between two points of the plane with Cartesian coordinates and is
This is the Cartesian version of Pythagoras's theorem. In three-dimensional space, the distance between points and is
which can be obtained by two consecutive applications of Pythagoras' theorem.
The Euclidean transformations or Euclidean motions are the (bijective) mappings of points of the Euclidean …
History
The adjective Cartesian refers to the French mathematician and philosopher René Descartes, who published this idea in 1637 while he was resident in the Netherlands. It was independently discovered by Pierre de Fermat, who also worked in three dimensions, although Fermat did not publish the discovery. The French cleric Nicole Oresme used constructions similar to Cartesian coordinates well before the time of Descartes and Fermat.
Description
Choosing a Cartesian coordinate system for a one-dimensional space—that is, for a straight line—involves choosing a point O of the line (the origin), a unit of length, and an orientation for the line. An orientation chooses which of the two half-lines determined by O is the positive and which is negative; we then say that the line "is oriented" (or "points") from the negative half towards the positive half. Then each point P of the line can be specified by its distance from O, taken with a …
Notations and conventions
The Cartesian coordinates of a point are usually written in parentheses and separated by commas, as in (10, 5) or (3, 5, 7). The origin is often labelled with the capital letter O. In analytic geometry, unknown or generic coordinates are often denoted by the letters (x, y) in the plane, and (x, y, z) in three-dimensional space. This custom comes from a convention of algebra, which uses letters near the end of the alphabet for unknown values (such as the coordinates of points in many geo…
Orientation and handedness
Fixing or choosing the x-axis determines the y-axis up to direction. Namely, the y-axis is necessarily the perpendicular to the x-axis through the point marked 0 on the x-axis. But there is a choice of which of the two half lines on the perpendicular to designate as positive and which as negative. Each of these two choices determines a different orientation (also called handedness) of the Cartesian plane.
Representing a vector in the standard basis
A point in space in a Cartesian coordinate system may also be represented by a position vector, which can be thought of as an arrow pointing from the origin of the coordinate system to the point. If the coordinates represent spatial positions (displacements), it is common to represent the vector from the origin to the point of interest as . In two dimensions, the vector from the origin to the point with Cartesian coordinates (x, y) can be written as:
Applications
Cartesian coordinates are an abstraction that have a multitude of possible applications in the real world. However, three constructive steps are involved in superimposing coordinates on a problem application.
1. Units of distance must be decided defining the spatial size represented by the numbers used as coordinates.