
- Start from the root.
- Compare the searching element with root, if less than root, then recursively call left subtree, else recursively call right subtree.
- If the element to search is found anywhere, return true, else return false.
How do you create a binary search tree?
Let’s begin by first establishing some rules for Binary Search Trees:
- A parent node has, at most, 2 child nodes.
- The left child node is always less than the parent node.
- The right child node is always greater than or equal to the parent node.
How do you validate a binary search tree?
Validate Binary Search Tree
- Problem. In Validate Binary Search Tree problem we have given the root of a tree, we have to check if it is a binary search tree or not.
- Approach. First, we do inorder traversal of the given tree and store it in an array. ...
- Time complexity. O (n) as we are traversing each node only once.
- Space complexity. ...
What is an example of an optimal binary search tree?
Optimal Binary Search Tree. A set of integers are given in the sorted order and another array freq to frequency count. Our task is to create a binary search tree with those data to find the minimum cost for all searches. An auxiliary array cost [n, n] is created to solve and store the solution of subproblems.
What is the best balanced binary search tree to know?
To check if a Binary tree is balanced we need to check three conditions :
- The absolute difference between heights of left and right subtrees at any node should be less than 1.
- For each node, its left subtree should be a balanced binary tree.
- For each node, its right subtree should be a balanced binary tree.
How do binary search trees work?
Definition. A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node's left subtree and smaller than the keys in all nodes in that node's right subtree.
What is binary search tree with example?
The binary search tree is an advanced algorithm used for analyzing the node, its left and right branches, which are modeled in a tree structure and returning the value. The BST is devised on the architecture of a basic binary search algorithm; hence it enables faster lookups, insertions, and removals of nodes.
How do you find a node in a binary tree?
0:0512:24Find Node in Binary Tree - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo what we will need to do we need to find this node and return it note that we're talking about aMoreSo what we will need to do we need to find this node and return it note that we're talking about a generic binary tree which is not necessarily a binary search tree.
Where is binary search tree used?
1. IntroductionA binary tree is a tree data structure comprising of nodes with at most two children i.e. a right and left child. ... In computing, binary trees are mainly used for searching and sorting as they provide a means to store data hierarchically. ... A routing table is used to link routers in a network.More items...•
What is binary search tree in C++?
Binary search tree in C++ is defined as a data structure that consists of the node-based binary tree where each node consists of at most 2 nodes that are referred to as child nodes. This tree is also known as an ordered or sorted tree.
What is BST explain its traversal?
An inorder traversal first visits the left child (including its entire subtree), then visits the node, and finally visits the right child (including its entire subtree). The binary search tree makes use of this traversal to print all nodes in ascending order of value.
What is binary search tree?
The following is the definition of Binary Search Tree (BST) according to Wikipedia. Binary Search Tree is a node-based binary tree data structure which has the following properties: The left subtree of a node contains only nodes with keys lesser than the node’s key. The right subtree of a node contains only nodes with keys greater than ...
Is there a duplicate node in a binary search tree?
The left and right subtree each must also be a binary search tree. There must be no duplicate nodes. The above properties of Binary Search Tree provides an ordering among keys so that the operations like search, minimum and maximum can be done fast.
How to search a binary tree?
Data Structure - Binary Search Tree 1 The value of the key of the left sub-tree is less than the value of its parent (root) node's key. 2 The value of the key of the right sub-tree is greater than or equal to the value of its parent (root) node's key.
How to search for an element in a subtree?
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
What is the value of the key of the left sub-tree?
The value of the key of the left sub-tree is less than the value of its parent (root) node's key. The value of the key of the right sub-tree is greater than or equal to the value of its parent (root) node's key.
What is BST in a database?
BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.
What is binary search tree?
What is a Binary Search Tree? A tree is a data structure composed of nodes that has the following characteristics: Each tree has a root node at the top (also known as Parent Node) containing some value (can be any datatype). The root node has zero or more child nodes.
How many children does a binary search tree have?
This means that every node on its own can be a tree. A binary search tree (BST) adds these two characteristics: Each node has a maximum of up to two children. For each node, the values of its left descendent nodes are less than that of the current node, which in turn is less than the right descendent nodes (if any).
How many children does a subtree have?
One subtree (one child): You have to make sure that after the node is deleted, its child is then connected to the deleted node's parent. Two subtrees (two children): You have to find and replace the node you want to delete with its inorder successor (the leftmost node in the right subtree).
What is breadth first search?
It begins at the root node and travels in a lateral manner (side to side), searching for the desired node. This type of search can be described as O (n) given that each node is visited once and the size of the tree directly correlates to the length of the search.
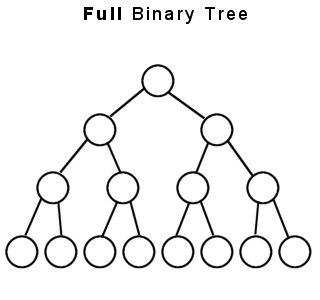
What is the number of leaf nodes in a binary tree?
In Full Binary Tree, number of leaf nodes is equal to number of internal nodes plus one. Complete Binary Tree: A Binary Tree is complete Binary Tree if all levels are completely filled except possibly the last level and the last level has all keys as left as possible.
How to search for an element in a subtree?
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Where to find successors in a tree?
To find the successor of the current node, look at the left-most/smallest leaf node in the right subtree.
Binary Search Trees
A binary search tree (BST) provides a way to implement a symbol table that combines the flexibility of insertion in linked lists with the efficiency of searching in an ordered array. BSTs are a dynamic data structure that is fast to both search and insert.
The Vocabulary of Trees
The words we use to describe trees in computer science employs a strange mixture of imagery...
Basic Operations on A BST
Special Types of Bt
Runtime
- Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Let's Look at A Couple of Procedures Operating on Trees.
Pre-Order
- Create: creates an empty tree.
- Insert: insert a node in the tree.
- Search: Searches for a node in the tree.
- Delete: deletes a node from the tree.
Post-Order
- Heap
- Red-black tree
- B-tree
- Splay tree