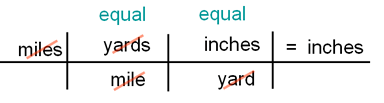
What is an example of dimensional analysis?
Example Of Dimensional Analysis For using a conversion factor, it is necessary that the values must represent the same quantity. For example, 60 minutes is the same as 1 hour, or 1000 meters is the same as 1 kilometer, or 12 months is the same as 1 year.
What is the length of 1 cm in meters?
5. 1 centimeter=1 meter=0.01 meter, or 1 cm =1100100 m = 0.01 m 6. 1 kilogram = 1,000 grams, or 1 kg = 1,000 g 7. 1 kilometer = 1,000 meters, or 1 km = 1000 m
What are the limitations of dimensional analysis?
Dimensional analysis is used to derive formulas. ● The dimensional analysis doesn't provide information about the dimensional constant. ● Dimensional analysis cannot derive trigonometric, exponential, and logarithmic functions.
How do you know if a dimensional relation is correct?
The dimensional relation will be correct if the L.H.S and R.H.S of an equation have identical dimensions. If the dimensions on two sides are incorrect, then the relations will also be incorrect. Dimensional analysis is used to convert the value of a physical quantity from one system of units to another system of units.

How many meters is a mile?
1609.34 metersAnswer: 1 mile is 1609.34 meters. To find the approximate distance in miles, multiply the length value by 1609.
How many meters are in a mile in scientific notation?
Let's start with the bare facts. One mile is the same as 1609.344 meters (or 'metres', if you're British). This means that 5 miles is 8046.72m and 10 miles is 16093.44m. To convert miles into meters, you simply multiply the number of miles by the number of meters in a mile: Number of miles × 1609.344m.
How many meters are in a mile in chemistry?
There are exactly 1609.344 meters in a mile.
How many feet is a mile dimensional analysis?
How Many Feet Are in a Mile? There are 5,280 feet in a mile, which is why we use this value in the formula above.
What are miles measured in?
5,280 feetmile, any of various units of distance, such as the statute mile of 5,280 feet (1.609 km). It originated from the Roman mille passus, or “thousand paces,” which measured 5,000 Roman feet. About the year 1500 the “old London” mile was defined as eight furlongs.
How do you convert meters to miles formula?
To convert meters to mile, use this formula: m/1,609.344=mi (meters divided by 1,609.344 equals miles).
How do you measure one mile?
Now that you know the stride of your step in feet, you can calculate a mile. There are 5,280 feet in one mile. Simply divide 5,280 feet by your average stride length to learn how many steps it will take to walk a mile. If your average stride length is 2 feet, for example, it will take 2,640 steps to walk a mile.
Is meters a mile or meter?
There are 1609.344 meters (m) in 1 mile. A meter, or metre, is the base unit of length in the International System of Units (SI). A mile is a measurement of length in the US customary and imperial systems of measurement.
What is Mi in the metric system?
The mile is a linear measurement of length equal to exactly 1,609.344 meters. One mile is also equal to 5,280 feet or 1,760 yards. The mile is a US customary and imperial unit of length.
How many blocks is a mile?
How many blocks are in a mile. From our sample size below using major cities, the average number of blocks in a mile would be 20.3 blocks. However, blocks can vary dramatically between each city or even direction.
How many football fields make a mile?
How many football fields are there in a mile? It would take 17.6 football fields laid end to end to travel a mile.
How many feet is a linear mile?
The mile is a linear measurement of length equal to exactly 1,609.344 meters. One mile is also equal to 5,280 feet or 1,760 yards.
How do you write meters in scientific notation?
As an example, the distance from Earth to the Sun is about 150,000,000,000 meters – a very large distance indeed. In scientific notation, the distance is written as 1.5 × 1011 m. The coefficient is the 1.5 and must be a number greater than or equal to 1 and less than 10.
What does m stand for in scientific notation?
As an example, the distance from Earth to the Sun is about 150,000,000,000 meters—a very large distance indeed. In scientific notation, the distance is written as 1.5×1011m. The coefficient is the 1.5 and must be a number greater than or equal to 1, and less than 10.
How do you convert to scientific notation?
0:171:53Converting to Scientific Notation - MathHelp.com - Math Help - YouTubeYouTubeStart of suggested clipEnd of suggested clipTo write a number in scientific notation. First write a decimal point in the numbers so that there'sMoreTo write a number in scientific notation. First write a decimal point in the numbers so that there's only one digit to the left of the decimal point.
How do you write scientific notation?
A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10. For example, 650,000,000 can be written in scientific notation as 6.5 ✕ 10^8.
What is dimensional analysis?
Dimensional analysis is used to represent the nature of physical quantity. The expressions of dimensions can be manipulated as algebraic quantities. Dimensional analysis is used to derive formulas.
Why is dimensional analysis important?
Dimensional analysis is used mainly because of five reasons, they are: To check the correctness of an equation or any other physical relation based on the principle of homogeneity.
What are the limitations of dimensional analysis?
Some major limitations of dimensional analysis are: ● The dimensional analysis doesn't provide information about the dimensional constant. ● Dimensional analysis cannot derive trigonometric, exponential, and logarithmic functions. ● Dimensional analysis doesn't give information about the scalar or vector identity of a physical quantity.
What does the principle of dimensions mean?
This principle depicts that, “the dimensions are the same for every equation that represents physical units. If two sides of an equation don’t have the same dimensions, it cannot represent a physical situation.”
Why is it important to know about dimensions?
To solve the mathematical problems of physical quantities, it is important to have a brief knowledge about units and dimensions. The basic concept of dimensions is that, only those quantities can be added or subtracted which have the same dimension. This concept helps us to derive relationships between physical quantities.
What is the dimensional formula of kinetic energy?
Therefore, the dimensional formula of kinetic energy is represented by [M1 L2 T-2].
How to do dimensional analysis?
Performing dimensional analysis is a pretty easy process. All you have to do is set up a series of fractions where the units end up canceling out. Remember, when you have fractions and want something to cancel out, you have to make sure it is present in both the numerator and denominator. Here’s a basic example of converting from feet to inches that uses the conversion factor of 1 foot = 12 inches.
What is dimensional analysis in chemistry?
In chemistry, a lot of your dimensional analysis will involve the number of molecules and atoms involved in a reaction (these calculations are called stoichiometry). Using the given information, use the skills of dimensional analysis to answer the following question.
How to manipulate units?
The process of manipulating our units is called dimensional analysis. This uses the principle that we can multiply a number by fractions that are equivalent to 1 to change the units without changing the actual value of the number. An easy way to think of this is to imagine a ruler that has inches on one side and centimeters on the other. If we measure a piece of string with either side, we get two different numbers with different units, but they represent the same real world length. That is the goal of dimensional analysis: to get the same real world value represented with different units.
How much lead is 11.3 g/ml?
For word problems, a necessary conversion factor is almost always given in the problem itself. In this case, 11.3 g/mL can help us find the mass of 45 mL of lead. We also need the fact that 1000 grams is equivalent to 1 kilogram.
Is 12 inches the same as 1 foot?
Pay careful attention to your conversion factors here. While we know that 12 inches is the same as 1 foot, notice that we are dealing with cubic inches. So, we have to cube all our numbers and units to get units that will actually cancel out.
When did the metric system start?
The Metric System had its beginnings back in 1670 by a mathematician called Gabriel Mouton. The modern version, (since 1960) is correctly called "International System of Units" or "SI" (from the French "Système International"). The metric system has been officially sanctioned for use in the United States since 1866, but it remains the only industrialized country that has not adopted the metric system as its official system of measurement. Many sources also cite Liberia and Burma as the only other countries not to have done so.
How many square feet are there in a 3 ft by 4 ft rectangle?
12 square feet = 12 ft2 means 12 squares 1 foot by 1 foot. The measure of the area of a rectangle 3 ft by 4 ft is 12 ft2 since it can be covered (tiled) with 12 squares each 1 foot by 1 foot.

Unit Conversion
- Dimensional analysis is also called a Unit Factor Method or Factor Label Method because a conversion factor is used to evaluate the units. For example, suppose we want to know how many meters there are in 4 km. Normally, we calculate as- 1 km = 1000 meters 4 km = 1000 × 4 = 4000 meters (Here the conversion factor used is 1000 meters)
Principle of Homogeneity of Dimensional Analysis
- This principle depicts that, “the dimensions are the same for every equation that represents physical units. If two sides of an equation don’t have the same dimensions, it cannot represent a physical situation.” For example, in the equation [MaLbTc] = MxLyTz As per this principle, we have a = x, b = y, and c = z
Example of Dimensional Analysis
- For using a conversion factor, it is necessary that the values must represent the same quantity. For example, 60 minutes is the same as 1 hour, 1000 meters is the same as 1 kilometre, or 12 months is the same as 1 year. Let us try to understand it in this way. Imagine you have 15 pens and you multiply that by 1, now you still have the same number of 15 pens. If you want to find ou…
Applications of Dimensional Analysis
- Dimensional analysis is an important aspect of measurement, and it has many applications in Physics. Dimensional analysis is used mainly because of five reasons, which are: 1. To check the correctness of an equation or any other physical relation based on the principle of homogeneity. There should be dimensions on two sides of the equation. The dimensional relation will be corre…
Limitations of Dimensional Analysis
- Some major limitations of dimensional analysis are: 1. Dimensional analysis doesn't provide information about the dimensional constant. 1. Dimensional analysis cannot derive trigonometric, exponential, and logarithmic functions. 1. It doesn't give information about the scalar or vector identity of a physical quantity.
Example of Dimensional Formula: Derivation For Kinetic Energy
- The dimensional formula of any physical entity is the mathematical expression representing the powers to which the fundamental units (mass M, length L, time T) are to be raised to obtain one unit of a derived quantity. Let us now understand the dimensional formula with an example. Now, we know that kinetic energy is one of the fundamental parts of Physics, hence its formula plays …
Derivation
- Kinetic energy (K.E) is given by = 12 [Mass x Velocity2]---- (I) The dimensional formula of Mass is =[M1L0T0]--- (ii) We know that, Velocity = Distance × Time-1 = Lx T-1(dimensional formula) Velocity has a dimensional formula [M0L1T-1]----- (iii) On substituting equation (ii) and iii) in the above equation (i) we get, Kinetic energy (K.E) = 12[Mass x Velocity2] Or, K.E = [M1L0T0] [M0L1…
Solved Example
- 1. Find out how many feet are there in 300 centimeters (cm). Ans.We need to convert cm into feet. Firstly, we have to convert cm into inches, and then inches into feet, as we can't directly convert cm into feet. The calculation of two conversion factors is required here: Then, 300 cm = 300 x 130.48 feet = 9.84 feet