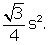
How many equilateral triangles are there in an icosahedron?
These lower symmetries allow geometric distortions from 20 equilateral triangular faces, instead having 8 equilateral triangles and 12 congruent isosceles triangles . These symmetries offer Coxeter diagrams: and respectively, each representing the lower symmetry to the regular icosahedron , (*532), [5,3] icosahedral symmetry of order 120.
What is icosahedron?
Icosahedron. Definition: An icosahedron is a regular polyhedron with 20 congruent equilateral triangular faces. It is one of the five Platonic solids. Try this Click on the figure to stop rotation. Drag anywhere to rotate. An icosahedron is a regular polyhedron that has 20 faces. All the faces are equilateral triangles and are all congruent,...
How many different shapes of icosahedra are there?
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex, non- stellated) regular icosahedron —one of the Platonic solids —whose faces are 20 equilateral triangles.
How many edges does a truncated icosahedron have?
1 The truncated icosahedron is an Archimedean solid. 2 Its face has two or more types of regular polygons. 3 It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices, and 90 edges. 4 It is the shape used in constructing soccer balls where white hexagons and black pentagons are joined together. More items...

How many triangle faces does an icosahedron have?
20 facesThe 20 faces of the icosahedron are equilateral triangles; they meet in 30 edges and 12 vertices.
How many does a icosahedron have?
20 facesIn geometry, a regular icosahedron (/ˌaɪkɒsəˈhiːdrən, -kə-, -koʊ-/ or /aɪˌkɒsəˈhiːdrən/) is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
How many edges are in a icosahedron?
30Icosahedron / Number of edges
What shapes make up a icosahedron?
The icosahedron is made up of twenty triangular faces. It has twelve vertices (five triangles meet at each vertex) and thirty edges. Using origami, one can combine platonic solids to create intricate stars or compounds. An example of this is the interlocking tetrahedra which is created from five tetrahedra.
What is a 20 faced shape called?
An Icosahedron is a 3D shape that has 20 faces. The name comes from the Greek word eikosi, meaning 'twenty', and hedra, meaning 'seat'.
What's a shape with 20 sides called?
In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.
What is special about icosahedron?
, the golden ratio. The solid therefore consists of 20 equilateral triangles. The symmetry of their arrangement is such that the resulting solid contains 12 pentagrams.
How do you make an icosahedron?
0:593:18How to Construct an Icosahedron - YouTubeYouTubeStart of suggested clipEnd of suggested clipPoints we create a top Pentagon plane. We can connect the vertices of the top and bottom planes withMorePoints we create a top Pentagon plane. We can connect the vertices of the top and bottom planes with a line moving in a zigzag formation. As you can see this forms the body of their Casa.
Why is icosahedron water?
The icosahedron represents the WATER element, symbolizing dreams, intuition, and emotions. Compared to the sharpness of the tetrahedron which is associated with the sharpness of spicy foods, the icosahedron's much duller angles make it the closest in shape to the sphere.
What is a 33 sided shape called?
What is the name of a polygon with…?#Name of the Polygon + Geometric Drawing33 sidestritriacontagon34 sidestetratriacontagon35 sidespentatriacontagon36 sideshexatriacontagon54 more rows
What is a 12 sided shape called?
dodecagonA dodecagon is a 12-sided polygon. Several special types of dodecagons are illustrated above. In particular, a dodecagon with vertices equally spaced around a circle and with all sides the same length is a regular polygon known as a regular dodecagon.
What shape is a d12?
rhombic dodecahedronThe standard form of the d12 is a regular dodecahedron, which is a Platonic solid whose faces are twelve regular pentagons. The sum of the numbers on opposite faces is usually 13. A d12 shaped like a rhombic dodecahedron.
What is a 10 sided dice called?
Pentagonal trapezohedronCommon variationsFaces/ SidesShape8Octahedron10Pentagonal trapezohedron12Dodecahedron20Icosahedron2 more rows
What is a 12 sided 3d shape called?
In geometry, a dodecahedron (Greek δωδεκάεδρον, from δώδεκα dōdeka "twelve" + ἕδρα hédra "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid.
What does icosahedron symbolize?
The Icosahedron is the fifth and final platonic solid having 20 triangular sides and symbol for the element of water. Meaning: trust in the wisdom of the universe is needed with a willingness to allow others to assist in the situation versus pursuing an active role. As the water suggests, it time to go with the flow.
How many faces can an icosahedron have?
20Icosahedron / Number of faces
How many faces does an icosahedron have?
It is one of the five platonic solids with equilateral triangular faces. Icosahedron has 20 faces, 30 edges, and 12 vertices. It is a shape with the largest volume among all platonic solids for its surface area. It has the most number of faces among all platonic solids. Icosahedron's vertices.
What Is an Icosahedron in Geometry?
It is a platonic solid constituting 20 faces, 30 edges, and 12 vertices.
Who Discovered the Icosahedron?
Athenian mathematician Theatetus (c. 417–369 BC) discovered regular icosahedron along with the octahedron. These two platonic solids are known to be discovered by Theatetus, while the other three were discovered by Plato.
What Is the Difference Between Icosahedron and Icosagon?
An icosahedron is a three-dimensional shape while Icosagon is a two-dimensional shape.
What is an icosahedron?
It is one of the five platonic solids with equilateral triangular faces.
What is the truncated icosahedron?
The truncated icosahedron is the base model of the Buckminsterfullerene.
How many faces does a platonic solid have?
The tetrahedron, cube, octahedron, icosahedron, and dodecahedron are the only five platonic solids. An icosahedron is the only platonic solid with 20 faces. This is the maximum number of faces a platonic solid can have.
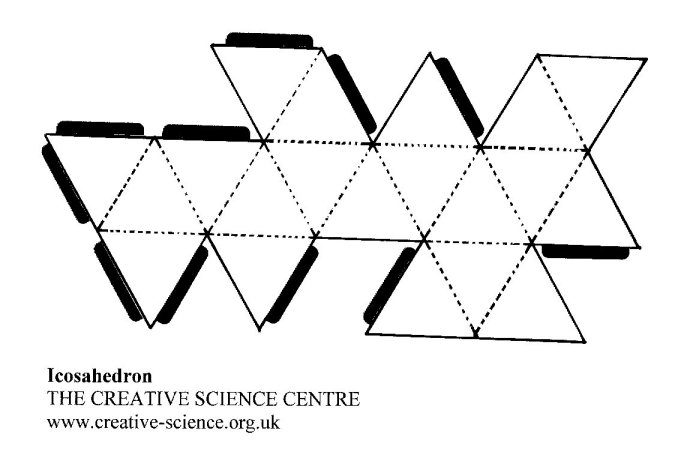
How many nets does an icosahedron have?
The Net of the Icosahedron. An icosahedron has 43,380 distinct nets. These are all the ways 20 equilateral triangles can be arranged to fold into the icosahedron. Here is one: The Icosahedron has: 15 2-fold axes. 10 3-fold axes. Six 5-fold axes.
What is the icosahedron associated with?
The icosahedron is associated with ‘Water ’. To Plato, water was the densest and least penetrating of the three fluid elements: fire, water and air. In modern times the large-scale clustering of tetrahedral water molecules have been found to take the shape of an icosahedron. We discuss this in detail in Article 173.
What element is the icosahedron?
In chemistry, in the work of Dr. Robert Moon, the icosahedron is the element Iron.
How many close packed spheres are in an icosahedron?
The icosahedron (and its dual the dodecahedron) can also be made from 32 close-packed spheres.
What is the ratio of a rectangle drawn inside an icosahedron?
A rectangle drawn inside an icosahedron has edges in the ratio φ:1 (or 1:φ).
Which scientist showed that tetrahedral water molecules form icosahedral clusters?
The work of Martin Chaplin shows us that tetrahedral water molecules form icosahedral clusters, linking modern science with ancient philosophy.
When was the truncated icosahedron discovered?
The Truncated Icosahedron is also the shape of the Fullerene molecule (Buckyball), an allotrope of carbon, discovered in 1985.
What is the icosahedron?
For example, the icosahedron is {3,5+} 1,0, and pentakis dodecahedron, {3,5+} 1,1 is seen as a regular dodecahedron with pentagonal faces divided into 5 triangles.
What is the symbol for a polyhedron?
In Magnus Wenninger 's Spherical models, polyhedra are given geodesic notation in the form {3,q+}b,c, where {3,q} is the Schläfli symbol for the regular polyhedron with triangular faces, and q- valence vertices. The + symbol indicates the valence of the vertices being increased. b,c represent a subdivision description, with 1,0 representing the base form. There are 3 symmetry classes of forms: {3,3+} 1,0 for a tetrahedron, {3,4+} 1,0 for an octahedron, and {3,5+} 1,0 for an icosahedron .
How are geodesic polyhedra made?
Geodesic polyhedra are constructed by subdividing faces of simpler polyhedra, and then projecting the new vertices onto the surface of a sphere. A geodesic polyhedron has straight edges and flat faces that approximate a sphere, but it can also be made as a spherical polyhedron (a tessellation on a sphere) with true geodesic curved edges on the surface of a sphere and spherical triangle faces.
What is a geodesic polyhedron?
A geodesic polyhedron is a convex polyhedron made from triangles. They usually have icosahedral symmetry, such that they have 6 triangles at a vertex, except 12 vertices which have 5 triangles. They are the dual of corresponding Goldberg polyhedra with mostly hexagonal faces.
How to define a polyhedron?
An icosahedron and related symmetry polyhedra can be used to define a high geodesic polyhedron by dividing triangular faces into smaller triangles, and projecting all the new vertices onto a sphere. Higher order polygonal faces can be divided into triangles by adding new vertices centered on each face. The new faces on the sphere are not equilateral triangles, but they are approximately equal edge length. All vertices are valence-6 except 12 vertices which are valence 5.
How to get subgrids in class 3?
The subgrids can be extracted by looking at a triangular tiling, positioning a large triangle on top of grid vertices and walking paths from one vertex b steps in one direction, and a turn, either clockwise or counterclockwise, and then another c steps to the next primary vertex.
How to find frequency of a polyhedron?
The frequency of a geodesic polyhedron is defined by the sum of ν = b + c. A harmonic is a subfrequency and can be any whole divisor of ν. Class II always have a harmonic of 2, since ν = 2 b .