how was the word trigonometry derived

Full Answer

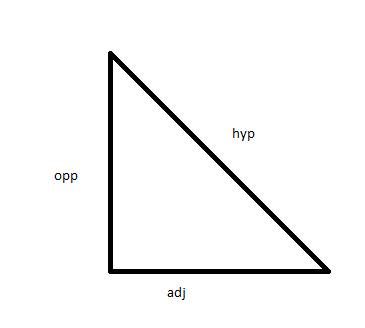
What is the best way to learn trigonometry?

What is the easiest way to learn trigonometry?

• Step 1: Review your all basics.
• Step 2: Start with the right angle triangles. …
• Example: A right angle have two sides 5 cm and 3 cm find the hypotenuse.
• Solution: Given opposite =5cm and adjacent=3 cm.
• Using Pythagoras theorem. …
• Step 4: Learn the other important function of trigonometry.

What is the history of trigonometry?

The history of trigonometry. In the earliest times, when at sea all terrestrial landmarks had disappeared, the last means available to mariners were the stars. Trigonometry was developed early in the history of mankind, because it allowed a reading of heaven essential to navigation.

What is the origin of the of the word trigonometry?

What is the meaning of the word trigonometry? The word trigonometry comes from the Greek words trigonon (“triangle”) and metron (“to measure”). For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated.

Which are the six functions in trigonometry?

These are:

• Cosecant (csc)
• Secant (sec)
• Cotangent (cot)

How old is the word trigonometry?

Trigonometry (from Ancient Greek τρίγωνον (trígōnon) 'triangle', and μέτρον (métron) 'measure') is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.

Who is the father of trigonometry?

The first trigonometric table was apparently compiled by Hipparchus, who is consequently now known as "the father of trigonometry".

Which country invented trigonometry?

The Babylonians could measure angles, and are believed to have invented the division of the circle into 360º. However, it was the Greeks who are seen as the original pioneers of trigonometry.

Who discovered sin?

Sine was introduced by Abu'l Wafa in 8th century, as a more convenient function, and gradually spread first in the Muslim world, and then to the West. (But apparently it was used in India centuries before him), as a more convenient function. However this new notation was adopted very slowly, it took centuries.

Where does trigonometry come from?

The word trigonometry comes from the Greek words trigonon (“triangle”) and metron (“to measure”). Until about the 16th century, trigonometry was chiefly concerned with computing the numerical values of the missing parts of a triangle (or any shape that can be dissected into triangles) when the values of other parts were given. For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated. Such calculations distinguish trigonometry from geometry, which mainly investigates qualitative relations. Of course, this distinction is not always absolute: the Pythagorean theorem, for example, is a statement about the lengths of the three sides in a right triangle and is thus quantitative in nature. Still, in its original form, trigonometry was by and large an offspring of geometry; it was not until the 16th century that the two became separate branches of mathematics.

Who was the first person to use trigonometry?

See all videos for this article. The first major ancient work on trigonometry to reach Europe intact after the Dark Ages was the Almagest by Ptolemy ( c. 100–170 ce ). He lived in Alexandria, the intellectual centre of the Hellenistic world, but little else is known about him.

How many trigonometric functions are there in a right triangle?

These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly.

What is a triangle inscribed in a circle?

He considered every triangle—planar or spherical—as being inscribed in a circle, so that each side becomes a chord (that is, a straight line that connects two points on a curve or surface, as shown by the inscribed triangle ABC in the figure).

What was Hipparchus' main interest in trigonometry?

This became the chief task of trigonometry for the next several centuries. As an astronomer, Hipparchus was mainly interested in spherical triangles, such as the imaginary triangle formed by three stars on the celestial sphere, but he was also familiar with the basic formulas of plane trigonometry.

What are the functions of an angle?

trigonometry, the branch of mathematics concerned with specific functions of angles and their application to calculations. There are six functions of an angle commonly used in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly. These functions are properties of the angle A independent of the size of the triangle, and calculated values were tabulated for many angles before computers made trigonometry tables obsolete. Trigonometric functions are used in obtaining unknown angles and distances from known or measured angles in geometric figures.

Where did trigonometry originate?

However, the systematic study of trigonometry dates to the middle ages in Hellenistic India where it began to spread across the Greek empire and bled into Latin territories during the Renaissance. With the Renaissance came an enormous growth of mathematics.

When was trigonometry first used?

The earliest known "strong" example of trigonometry is found on the Rhind Mathematical Papyrus which dates to around 1650 BC.

What are some examples of trigonometric functions?

Hyperbolae and ellipses serve as great examples of how trigonometry can quickly deviate from just stating the Pythagorean Theorem and the few relationships between the lengths of the sides of a simple triangle (the trig functions.)

What is trigonometry in math?

What is Trigonometry: Trigonometry is the branch of mathematics devoted explicitly to the relationship between the sides and angles of triangles. Its name even sounds triangle-y and for a good reason: the word trigonometry is derived from two Greek words - 'trigonon' which means 'triangle' and 'metron' meaning 'measure.'.

How many functions are there in a right triangle?

In a right triangle, six functions can be used to relate the lengths of its sides with an angle (θ.) The three ratios sine, cosine, and tangent are reciprocals of the ratios cosecant, secant, and cotangent respectively, as shown: pinterest-pin-it.

How to find radii and arcs of a circle?

Let's start with a circle. One of the first things one learns in trigonometry is that the radii and arcs of a circle can be found using a right triangle. This is because the hypotenuse of a right triangle is also the slope of the line connecting the center of the circle with a point on the circle (as shown below.)

Can conics be used in trigonometry?

Geometric Curves: Conics in Trig. As mentioned above, trigonometry is powerful enough to make measurements of things that are not triangles. Conics such as hyperbolae and ellipses are examples of how awesomely sneaky trigonometry can be -- a triangle (and all its formulae) can be hidden inside an oval!

What does trigonometry mean?

Therefore, the meaning of trigonometry is measuring a triangle. A triangle contains angles and sides basically. So, measuring angles, sides and investigating relation between them is called Trigonometry.

How many functions are there in trigonometry?

There are six functions in trigonometry and each trigonometric function is defined on the basis of ratio between any two sides of the triangle. Hence, every function is also called as trigonometric ratio simply.

What is trigonometric study?

The study of the properties and uses of trigonometric functions.

What percentage of people never use trigonometry?

Less than 2 percent of respondents said that they use trigonometry in their daily life, but over 70 percent of them said that they never use it.

What is the branch of mathematics that deals with the relations between the sides and angles of plane or spherical?

trigonometry . the branch of mathematics that deals with the relations between the sides and angles of plane or spherical triangles, and the calculations based on them.

Where does the word "infant" come from?

The word "infant" comes from the Latin word "infans" which literally means "unable to speak; speechless."

Why is the word "sinister" Latin?

The word "sinister" is Latin for "left," because left-handed people were often thought of as suspicious, evil, or demonic.

When was trigonometry first used?

Trigonometry began during the Third Century B.C. At this time, geometry concepts were used for astronomical studies only. The word trigonometry was derived from two Greek words. Trigonometry is from the word trigonon, meaning triangle, and the word metron, meaning measure. Trigonometry studies involve the lengths of sides and angles of triangles. The early astronomers of this time period first discovered that the lengths of the sides of a right-angle triangle and the angles between those sides are correlated. Because of those relationships, if the length of at least one side and the value of one angle are known, then all other angles and lengths can be determined using a system of proportions. This branch of mathematics has had many contributions …show more content…

What is the name of the geometry that was invented to measure angles in the sky?

Mathematicians of antiquity were concerned with the measurement of angles in the skies, and the geometry invented to deal with this problem was called spherics and was studied as part of the quadrivium of study [1]. While spherics became elliptic geometry, trigonometry evolved in its own path. Any discussion of trigonometry, however, must discuss the concept of angle first. Degree measurement for angles was already in use by the Babylonians in the year 300 B.C.E. This civilization was the first to assign coordinates to stars.…

Who discovered Pascal's triangle?

A literature of Pascal’s Triangle emerged in 1068 discovered by Hindu mathematician Bhattotpala (c.1068) who recorded the first 16 rows of the triangle (Wilson, 2013, p170). Meanwhile, in Persia, Al-Karaji (953-1029) also found the binomial theorem according to Pascal’s Triangle as well as several theorems related to it (Coolidge, 1949, p151). Although the original work from Al-Karaji had lost, the later Persian mathematician Khayyam (1048-1122) referred Al-Karaji’s work about Pascal’s Triangle and uses it to find the nth roots according to the binomial expansion. Also around 11th century, Chinese mathematician Jia Xian (1010-1070) used Pascal’s Triangle to extract square roots and cube roots – more details will be mentioned later in this paper. He wrote down his discovery in the book Shi Shuo Suan Shu [The key to Mathematics].…

What is trigonometry used for?

Trigonometry is an important branch of mathematics that is used to study the relationship between ratios of the sides of a right-angled triangle with its angles. The word “trigonometry” is derived from the Greek words, “trigon” and “metron”. The word “trigon” means a triangle and the word ”metron” means a measure. Hence, trigonometry means the science of measuring triangles. In broader cases it is that branch of mathematics which deals with the measurement of the sides and the angles of a triangle and the problems allied with the angles.

What are Trigonometric Ratios?

Consider an acute angle ∠YAX = θ with initial side AX and terminal side AY. Let P be any point on the terminal side AY. Draw PM perpendicular from P on AX to get the right angled triangle AMP in which ∠PAM = θ.

What happens to the lengths of the trigonometric ratios if we choose P somewhere else on AY?

The above trigonometric ratios, as we can see depend upon the value of angle θ and are independent of the position of the point P on the terminal side AY of the acute angle ∠XAY. This means that if we choose P somewhere else on AY, then the lengths PM, AM and AP will change. However, the trigonometric ratios will remain same. Hence we can say that –

What is the science of measuring triangles?

Trigonometry means the science of measuring triangles.

How many units are in a triangle with a hypotenuse?

So, we draw a triangle ABC, right angled at B such that Perpendicular = BC = 3 units and Hypotenuse = Ac = 5 units.

What is the bisector of angle A and D?

Since each angle of an equilateral triangle is 60 o, therefore, each angle of the triangle ABC will be equal to 60 o. Let AD be perpendicular from A on BC. Since the triangle is equilateral, therefore, AD is the bisector of angle A and D is the mid-point of BC.

What is the measure of an angle?

The measure of an angle is the amount of rotation from the initial side to the terminal side.

What is Trigonometry?

The word “Trigonometry” is derived from three Greek words i.e. Trio meaning thrice, Gonia meaning angle and Metron meaning measure. Literally, it means “measurement of triangles i.e., measuring the sides and angles of triangles”.

Positive and Negative Angles

In geometry, angles are always taken in the positive sense and their measures lie between 0° and 360° but in trigonometry, angles may be positive or negative and their measures may have any value.

Units of Measurement of Angles

There are three systems of units in which angles are measured. They are-

Length of an Arc of a Circle

Let ∠AOB be a given angle. With O as a centre and taking r as the radius (on a certain scale), a circle is drawn to cut OA at P and OB at Q respectively. Now, from the arc PQ, PC is cut off such that PC = r.O and C are joined. Let PQ = l.

It's More Than Just Triangles

The Early Roots of Trigonometry

• Defining the very beginning of a concept is difficult. Because mathematics is so abstract, we can't just say a cave painting of a triangle is trigonometry. What did the painter mean by the triangle? Did he just like triangles? Was he enthralled with how the length of one side, another side, and the angle they made dictated the length and angles of ...

See more on owlcation.com

The Trigonometric Functions

Geometric Curves: Conics in Trig

Equations For Ellipses

Equations For Hyperbolae

Comments