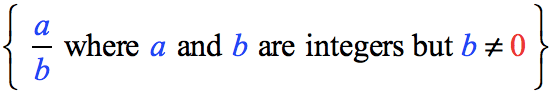
Integers can be expressed as rational numbers such as -3/1, -6/2 But rational numbers like -5/3, 8/11, 2/5, etc. are not integers as they don't simplify to give us a whole number (including negatives of the whole numbers). ⇒ All integers are rational numbers but all rational numbers are not integers.
Is 3 over 4 a rational number?
Similarly, q4, q5 are the rational numbers between ‘a’ and ‘b’ lie to the right of q1 as follows: Average of two numbers always lies between them. Let q1, q2, q3, q4, q5,.......... be the rational number between 3 and 4. In this way, we can find many rational numbers between 3 & 4 as given below.
How do you calculate rational numbers?
- – Once determined that it is a Rational Root, the root index should be identified.
- – Subsequently, the root of each element of the fraction, that is, of the Numerator and Denominator, must be calculated.
- – Finally, it will be searched if there is any way to simplify the obtained fraction.
Is 4 times pi a rational number?
Pi is an irrational number, same is pi/4. But then u will say that pi=22/7, then how is it irrational? actually, 22/7 is the closest approximation of the value of pi and not the actual value. Plz, upvote !!
Why is negative 8 a rational number?
A rational number is what happens when you divide one integer by another. For instance, .9 is a rational number because it comes from diving the 9 integer by the 10 integer. Hover for more information. Who are the experts?

Why are decimals considered rational numbers?
If you’re wondering why repeating decimals are considered rational numbers, the answer is that repeating decimals can be described as a ratio of two integers. So any decimal which uses repetitive numbers such as 0.575757 and 0.818181 will always be considered rational numbers. At the same time all numbers which repeat themselves continuously such ...
What is an integer in math?
In the study of mathematics an integer is not simply a number but a whole number, rather than a fractional number.
Is 0.36363 a rational number?
As while decimal figures which have unique numbers such as pi are irrational numbers, decimal numbers which have repeating numbers such as 0.36363 are rational numbers. Which means that 0.363636 is a prime example of a rational number that is not an integer. Further examples of rational numbers that are not integers: ...
Is a decimal an integer?
Now that you fully comprehend what an integer is, it will be easier to find a rational number that isn’t an integer. A great example to keep in mind is a decimal number, which has reoccurring, repeating decimal numbers. As while decimal figures which have unique numbers such as pi are irrational numbers, decimal numbers which have repeating numbers ...
Can integers be negative?
However, keep in mind that integers don ’t have to be positive and negative whole numbers can also be classified as integers. An example of a rational integer which is a negative number is -5.
Is there a term for a decimal that never ends?
There is actually an offical mathematical term for a decimal number which is infinite and never ends. In fact, both the terms reptend and repetend can be properly used in order to describe such numbers. Why is it important to be able to recognize rational numbers:
Classifying Integer, Whole, Rational, and Irrational Numbers
Step 1: Determine if the number has a decimal or fraction part. If it is already in fraction form, check if it simplifies to a non-fraction. If the number does not need a decimal or fraction part, it is an integer and a rational number. If it is written as a fraction, it is a rational number.
Classifying Integer, Whole, Rational, and Irrational Numbers - Vocabulary
Whole number: The whole numbers consist of 0 and the positive numbers that do not need a fraction or decimal part.
Types Of Numbers
There are different types of numbers categorized into sets by the number system. The types are described below,
What are Rational Numbers and Integers?
Rational numbers are of the form p/q, where p and q are integers and q ≠ 0. Because of the underlying structure of numbers, p/q form, most individuals find it difficult to distinguish between fractions and rational numbers.
Is Every Rational Number an Integer?
All rational numbers are not integer because as we know Rational numbers are of the form p/q, where p and q are integers and q ≠ 0. Because of the underlying structure of numbers, p/q form, most individuals find it difficult to distinguish between fractions and rational numbers.
Sample Problems
Question 1: Identify these numbers which are both rational and integer numbers?
