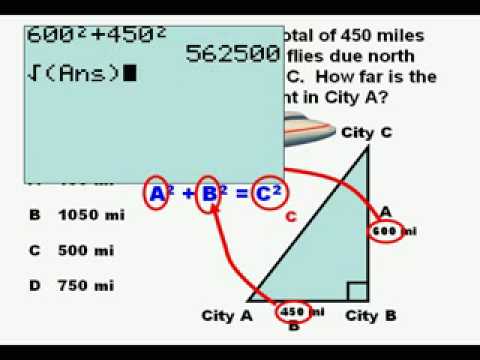
What are the lengths of the sides in a right triangle?
If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.
Which side lengths would not make a triangle?
Therefore, all you have to do is add together each combination of 2 sides to see if it's greater than the third side. If each combination is, the 3 side lengths are a triangle, but if one or more of them isn't, it's not a triangle. To see examples of how to apply the triangle equality theorem, keep reading!
Do these side lengths make a right triangle?
How do you tell if a triangle is a right triangle with side lengths? The converse of the Pythagorean Theorem is: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
How do you find the longest side of a triangle?
To find out which, first we give names to the sides:
- Adjacent is adjacent (next to) to the angle,
- Opposite is opposite the angle,
- and the longest side is the Hypotenuse.
What is the geometric place for the right angle in a right angle triangle?
Which side of the syringe has the longest side?
What is the maximum length of a secant?
What is the side opposite the right angle?
Is diameter twice radius?
Does Thales' theorem prove Pythagoras' theorem?
See 3 more
About this website
Which is the longest side of a right triangle Class 7?
hypotenuseIn a right triangle, hypotenuse is the longest side.
Is hypotenuse always the longest side?
The hypotenuse side of a right triangle is always across from the 90 degree angle (the little box). It is always the longest side of the triangle. The opposite and adjacent sides of a right triangle are the legs of the triangle and they form the 90 degree angle.
Is side C on a right triangle is always the longest?
2 Answers. Side A and B does not matter when your trying to apply this to the pythagorean theorem but side C must always be the hypotenuse. The hypotenuse is always the triangle's longest side.
How do you know which side is the longest?
The longest side in a triangle is opposite the largest angle, and the shortest side is opposite the smallest angle. Triangle Inequality: In any triangle, the sum of the lengths of any two sides is greater than the length of the third side. Pythagorean Theorem: In a right triangle with hypotenuse .
Is the hypotenuse the shortest?
The "c" is the hypotenuse, and although it represents the longest side of a right triangle, it is the shortest path between the two points on either end.
Is C always the biggest angle?
1 Expert Answer No, c is not necessarily the longest side. If the sides are called a, b, c, let C = angle opposite side c, let B = angle opposite side b, and let A be the angle opposite side a. a2+b2 = c2.
What side is always C?
the hypotenuseNOTE: The side “c” is always the side opposite the right angle. Side “c” is called the hypotenuse.
What letter is the longest side of a triangle?
The longest side of the right triangle is its hypotenuse i.e., the side opposite to the right angle. Q.
Why is hypotenuse always the longest side?
The hypotenuse is always the longest side of a right triangle because it is across from the right angle, which is 90 degrees. The other two angles cannot be more than 90 degrees so the right angle has to be the largest angle. Therefore, the side across from it is the longest side, which is the hypotenuse.
What is the longest side in Pythagoras?
the hypotenuseThe longest side of a right-angled triangle is the hypotenuse. The hypotenuse is always opposite the right angle.
What is the longest side of the Pythagoras Theorem?
the hypotenuse sidePythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°.
Why is hypotenuse longest side?
On a right triangle, two angles are acute and the third is a right angle. Hence the side opposite the right angle is the longest side.
Prove that in a right angled triangle, hypotenuse is the longest side.
Click here👆to get an answer to your question ️ Prove that in a right angled triangle, hypotenuse is the longest side.
trigonometry - Prove that the hypotenuse is the longest side in a right ...
From trig text. Given hint: is $ a^2 + b^2 > a^2 $. Pythagorean theorem,obviously. What would be an acceptable proof?
Relationship of sides to interior angles in a triangle - Math Open Ref
Recall that in a scalene triangle, all the sides have different lengths and all the interior angles have different measures. In such a triangle, the shortest side is always opposite the smallest angle. (These are shown in bold color above) Similarly, the longest side is opposite the largest angle.
What is the geometric place for the right angle in a right angle triangle?
I just wanted to illustrate the fact that the geometric place for the right angle in a right angle triangle is a half circle with the hypotenuse as diameter.
Which side of the syringe has the longest side?
And we have proved that the hypotenuse is the longest side.
What is the maximum length of a secant?
An even simpler proof: The maximum length a secant can have is the diameter . Thus (using the fact that the the geometric place for the right angle in a right-angled triangle is the circle with the hypotenuse as a diameter) the two cathetes are secants in the same circle.
What is the side opposite the right angle?
I'm using the definition that the hypotenuse is the side opposite the right angle.
Is diameter twice radius?
Now the diameter, , is twice the radius which is equal to . Therefore we have
Does Thales' theorem prove Pythagoras' theorem?
Not sure what your point is. Thales' theorem doesn't prove Pythagoras' theorem as far as I know.
Which triangle has 2 sides of equal length?
Another of special triangles is the isosceles triangle, which has 2 sides of equal length, and hence two angles of the same size. As opposed to the equilateral triangle, isosceles triangles come in many different shapes, but all have certain properties that are exploited by the isosceles triangle calculator to obtain all the parameters of these triangles.
What is a right triangle (or right-angled triangle)?
The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90°. The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.
How to find the base of a triangle if you don't know the height?
If you don't know the base or the height, you can find it using the Pythagorean theorem. Use the right triangle calculator to check your calculations or calculate the area of triangles with sides that have larger or decimal value length.
How to solve for hypotenuse in a right triangle?
To solve for c, take the square root of both sides to get c = √ (b²+a²).
What happens if you separate rectangles by diagonals?
If we separate the rectangle by the diagonal, what will we obtain is two right-angled triangles. Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. This means that the area of the rectangle is double that of each triangle.
What are the sets of numbers that satisfy the Pythagorean theorem?
These sets of numbers are called the Pythagorean triplets and are sets of 3 integers (let's call the a, b and c) and satisfy the Pythagorean theorem: a² + b² = c². That is, they could form a right triangle with sides of length a, b and c. The amount of numbers that satisfy this relationship is limited but mathematicians find joy in searching for new ones.
Why are the other two angles smaller than the right angle?
The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°. In a right angled triangle the sides are defined in a special way. The side opposing the right angle is always the biggest in the triangle and receives the name of "hypotenuse".
What is a right triangle?
A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.
What is the purpose of knowing the side of a 30°-60° 90° triangle?
As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily . This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.
What is the name of the triangle that divides the original triangle into two smaller triangles that are similar to the original?
The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle. If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle.
What are some examples of Pythagorean triples?
In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc. Area and perimeter of a right triangle are calculated in the same way as any other triangle.
What is the geometric place for the right angle in a right angle triangle?
I just wanted to illustrate the fact that the geometric place for the right angle in a right angle triangle is a half circle with the hypotenuse as diameter.
Which side of the syringe has the longest side?
And we have proved that the hypotenuse is the longest side.
What is the maximum length of a secant?
An even simpler proof: The maximum length a secant can have is the diameter . Thus (using the fact that the the geometric place for the right angle in a right-angled triangle is the circle with the hypotenuse as a diameter) the two cathetes are secants in the same circle.
What is the side opposite the right angle?
I'm using the definition that the hypotenuse is the side opposite the right angle.
Is diameter twice radius?
Now the diameter, , is twice the radius which is equal to . Therefore we have
Does Thales' theorem prove Pythagoras' theorem?
Not sure what your point is. Thales' theorem doesn't prove Pythagoras' theorem as far as I know.