
How do you calculate the central limit theorem?
μ = E ( X i) = r = 3. while the variance of a chi-square random variable with three degrees of freedom is: σ 2 = V a r ( X i) = 2 r = 2 ( 3) = 6. The Central Limit Theorem, therefore, tells us that the sample mean X ¯ is approximately normally distributed with mean: μ X ¯ = μ = 3. and variance: σ X ¯ 2 = σ 2 n = 6 n.
How to understand the central limit theorem?
What is the Central Limit Theorem?
- To begin, select groups of students from the class at random. ...
- Calculate each sample's individual mean.
- Calculate the average of these sample means.
- The value will give us the approximate average marks of the students in Class X.
- The histogram of the sample means marks of the students will resemble a bell curve or normal distribution.
When can you use central limit theorem?
The central limit theorem can be used to illustrate the law of large numbers. The law of large numbers states that the larger the sample size you take from a population, the closer the sample mean gets to μ .
What is so important about the central limit theorem?
- It can be used for making confidence intervals.
- It is able to disregard the distribution that some underlying X follows.
- The distribution of a sum approaches the normal distribution. This occurs while the distribution of terms in the underlying distribution are not necessarily normal.
Do you need a large sample for central limit theorem?
Before illustrating the use of the Central Limit Theorem (CLT) we will first illustrate the result. In order for the result of the CLT to hold, the sample must be sufficiently large (n > 30).
How do you know if a sample size is large enough for CLT?
In practice, some statisticians say that a sample size of 30 is large enough when the population distribution is roughly bell-shaped. Others recommend a sample size of at least 40.
How can we tell if the sample size is big enough before applying the central limit theorem?
The Large Enough Sample Condition tests whether you have a large enough sample size compared to the population. A general rule of thumb for the Large Enough Sample Condition is that n≥30, where n is your sample size. However, it depends on what you are trying to accomplish and what you know about the distribution.
When can you not use the central limit theorem?
If the sample size is at least 30 or the population is normally distributed, then the central limit theorem applies. If the sample size is less than 30 and the population is not normally distributed, then the central limit theorem does not apply.
What is the minimum sample size required for the central limit theorem?
30Sample size equal to or greater than 30 are required for the central limit theorem to hold true. A sufficiently large sample can predict the parameters of a population such as the mean and standard deviation.
What are the conditions of the central limit theorem?
It must be sampled randomly. Samples should be independent of each other. One sample should not influence the other samples. Sample size should be not more than 10% of the population when sampling is done without replacement.
Which of the following conditions regarding sample size must be met to apply the central limit theorem for simple proportions?
Which of the following conditions regarding sample size must be met to apply the Central Limit Theorem for Sample Proportions? To apply the Central Limit Theorem for Sample Proportions the sample size must be large enough that the sample expects at least 10 successes and 10 failures.
Why is a large sample size important?
The larger the study sample size, the smaller the margin of error.) Larger sample sizes allow researchers to control the risk of reporting false-negative or false-positive findings. The greater number of samples, the greater the precision of results will be.
Which sample size is enough?
The minimum sample size is 100 Most statisticians agree that the minimum sample size to get any kind of meaningful result is 100. If your population is less than 100 then you really need to survey all of them.
Why is 30 the minimum sample size?
“A minimum of 30 observations is sufficient to conduct significant statistics.” This is open to many interpretations of which the most fallible one is that the sample size of 30 is enough to trust your confidence interval.
What is the minimum sample size for statistical significance?
For example, in regression analysis, many researchers say that there should be at least 10 observations per variable. If we are using three independent variables, then a clear rule would be to have a minimum sample size of 30. Some researchers follow a statistical formula to calculate the sample size.
Which of the following is false about the central limit theorem?
It is false. The correct statement is: The central limit theorem states that if you have a population with mean and standard deviation and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. Thus, D is false.
How many samples do you need for the CLT?
30The central limit theorem (CLT) states that the distribution of sample means approximates a normal distribution as the sample size gets larger, regardless of the population's distribution. Sample sizes equal to or greater than 30 are often considered sufficient for the CLT to hold.
What is a sufficient sample size?
Most statisticians agree that the minimum sample size to get any kind of meaningful result is 100. If your population is less than 100 then you really need to survey all of them.
What's a large enough sample size?
Often a sample size is considered “large enough” if it's greater than or equal to 30, but this number can vary a bit based on the underlying shape of the population distribution. In particular: If the population distribution is symmetric, sometimes a sample size as small as 15 is sufficient.
How many samples are needed for the sample size to be considered as large?
Usually, researchers regard 100 participants as the minimum sample size when the population is large.
How large of a sample is sufficient for the central limit theorem?
There is no exact definition for how large a sample size needs to be in order for the central limit theorem to apply, but in general it depends on the skewness of the population distribution that the sample comes from: If the population distribution is symmetric, sometimes a sample size as small as 15 is sufficient.
What does the central limit theorem state about sampling distribution?
Recall that the central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is “large enough”, even if the population distribution is not normal.
How to find the variance of a sampling distribution?
2. The variance of the sampling distribution will be equal to the variance of the population distribution divided by the sample size: s2 = σ2 / n.
Why is the sampling distribution for the sample mean called the sampling distribution?
This is known as the sampling distribution for the sample mean because it shows the distribution of sample means.
What is the central limit theorem?
The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough, even if the population distribution is not normal.
What is the variance of a chi square distribution?
The variance of a chi-square distribution is 2 * df. In this case, σ2 = 2 * 3 = 6.
What is the sample size of a symmetric population?
If the population distribution is symmetric, sometimes a sample size as small as 15 is sufficient.
What is the sample size of the central limit theorem?
The sample size must be 30 or higher for the central limit theorem to hold. One of the most important components of the theorem is that the mean of the sample will be the mean of the entire population. If you calculate the mean of multiple samples of the population, add them up, and find their average, the result will be the estimate ...
Who coined the central limit theorem?
History of the Central Limit Theorem. The initial version of the central limit theorem was coined by Abraham De Moivre, a French-born mathematician. In an article published in 1733, De Moivre used the normal distribution to find the number of heads resulting from multiple tosses of a coin. The concept was unpopular at the time, ...
What is the variance of the sample distribution?
The variance of the sample distribution, on the other hand, is the variance of the population divided by n. Therefore, the larger the sample size of the distribution, the smaller the variance of the sample mean.
What is Bayes' theorem?
Bayes' Theorem The Bayes theorem (also known as the Bayes’ rule) is a mathematical formula used to determine the conditional probability of events. Central Tendency.
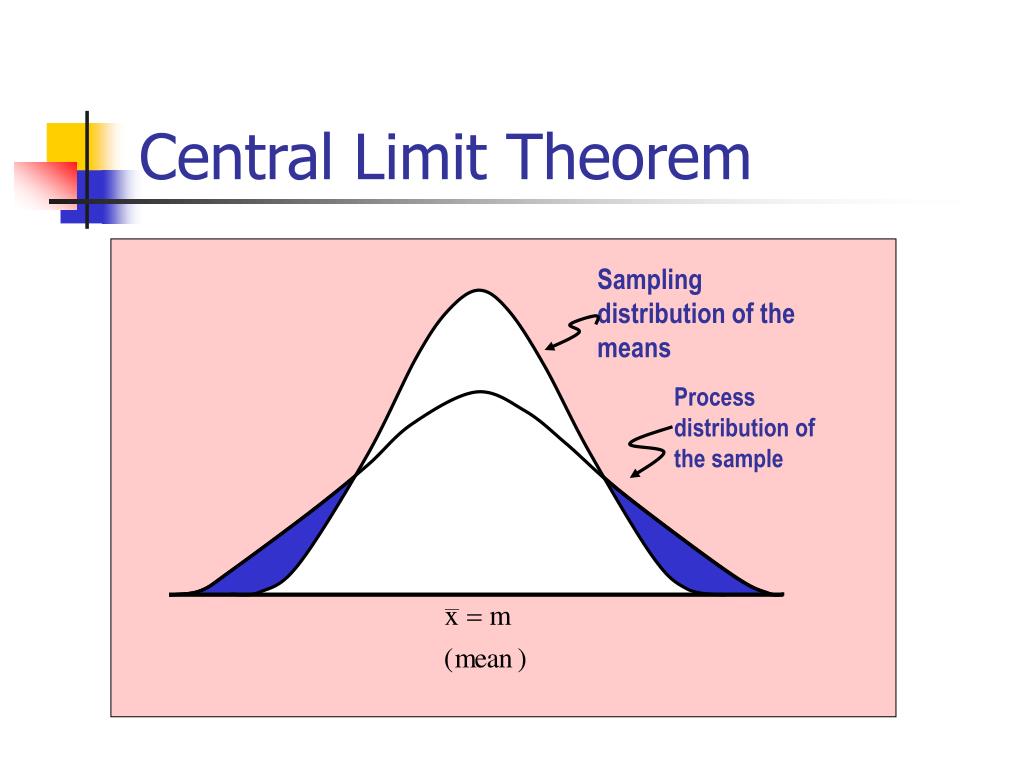
What happens to the distribution of the means from repeated samples?
As the sample sizes get bigger, the distribution of the means from the repeated samples tend to normalize and resemble a normal distribution. The result remains the same regardless of what the original shape of the distribution was. It can be illustrated in the figure below:
What is the law of large numbers?
Law of Large Numbers In statistics and probability theory, the law of large numbers is a theorem that describes the result of repeating the same experiment a large number of. Total Probability Rule.
How does randomized sampling work?
With the nature of randomized sampling, each sample will produce a different result. As you increase the size of the sample size with each sample you pick, the sample means will start forming their own distributions. The distribution of the sample means will move toward normal as the value of n increases.
What is the central limit theorem?
The central limit theorem in statistics states that, given a sufficiently large sample size, the sampling distribution of the mean for a variable will approximate a normal distribution regardless of that variable’s distribution in the population.
Why is the Central Limit Theorem Important?
The central limit theorem is vital in statistics for two main reasons—the normality assumption and the precision of the estimates.
How big of a sample size is needed for a skewed distribution?
The more the population distribution differs from being normal, the larger the sample size must be. Typically, statisticians say that a sample size of 30 is sufficient for most distributions. However, strongly skewed distributions can require larger sample sizes. We’ll see the sample size aspect in action during the empirical demonstration below.
Why does the standard deviation of the sampling distribution become smaller as the sample size increases?
As the sample size (n) increases, the standard deviation of the sampling distribution becomes smaller because the square root of the sample size is in the denominator. In other words, the sampling distribution clusters more tightly around the mean as sample size increases. Let’s put all of this together.
What happens to the sampling distribution as the sample size increases?
As the sample size increases, the sampling distributions more closely approximate the normal distribution and become more tightly clustered around the population mean —just as the central limit theorem states!
What is the shape of the sampling distribution?
The shape of the sampling distribution depends on the sample size. If you perform the study using the same procedure and change only the sample size, the shape of the sampling distribution will differ for each sample size. And, that brings us to the next part of the CLT definition!
What does CLT mean in population?
Specifically, the CLT states that regardless of the variable’s distribution in the population, the sampling distribution of the mean will tend to approximate the normal distribution.
How many failures are expected in the Central Limit Theorem?
To apply the Central Limit Theorem for Sample Proportions the sample size must be large enough that the sample expects at least 10 successes and 10 failures.
How big must a population be to be considered a sample?
The population size must be at least 10 times bigger than the sample size.
What is the probability that a sample proportion will fall within 2 standard errors of the population proportion?
The probability that a sample proportion will fall within 2 standard errors of the population proportion is 95%.
Can population proportion be replaced with sample proportion?
The population proportion p can be replaced with the sample proportion.
What Is The Central Limit Theorem?
Central Limit Theorem Formula
- Fortunately, you don’t need to actually repeatedly sample a population to know the shape of the sampling distribution. The parametersof the sampling distribution of the mean are determined by the parameters of the population: 1. The meanof the sampling distribution is the mean of the population. 1. The standard deviationof the sampling distribution is the standard deviation of th…
Sample Size and The Central Limit Theorem
- The sample size (n) is the number of observations drawn from the population for each sample. The sample size is the same for all samples. The sample size affects the sampling distribution of the mean in two ways.
Conditions of The Central Limit Theorem
- The central limit theorem states that the sampling distribution of the mean will always follow a normal distributionunder the following conditions: 1. The sample size is sufficiently large. This condition is usually met if the sample size is n ≥ 30. 1. The samples are independent and identically distributed (i.i.d.) random variables. This condition...
Importance of The Central Limit Theorem
- The central limit theorem is one of the most fundamental statistical theorems. In fact, the “central” in “central limit theorem” refers to the importance of the theorem.
Central Limit Theorem Examples
- Applying the central limit theorem to real distributions may help you to better understand how it works.