
Euclid's Postulates
- 1. A straight line segment can be drawn joining any two points.
- 2. Any straight line segment can be extended indefinitely in a straight line.
- 3. Given any straight lines segment, a circle can be drawn having the segment as radius and one endpoint as center.
- 4. All Right Angles are congruent.
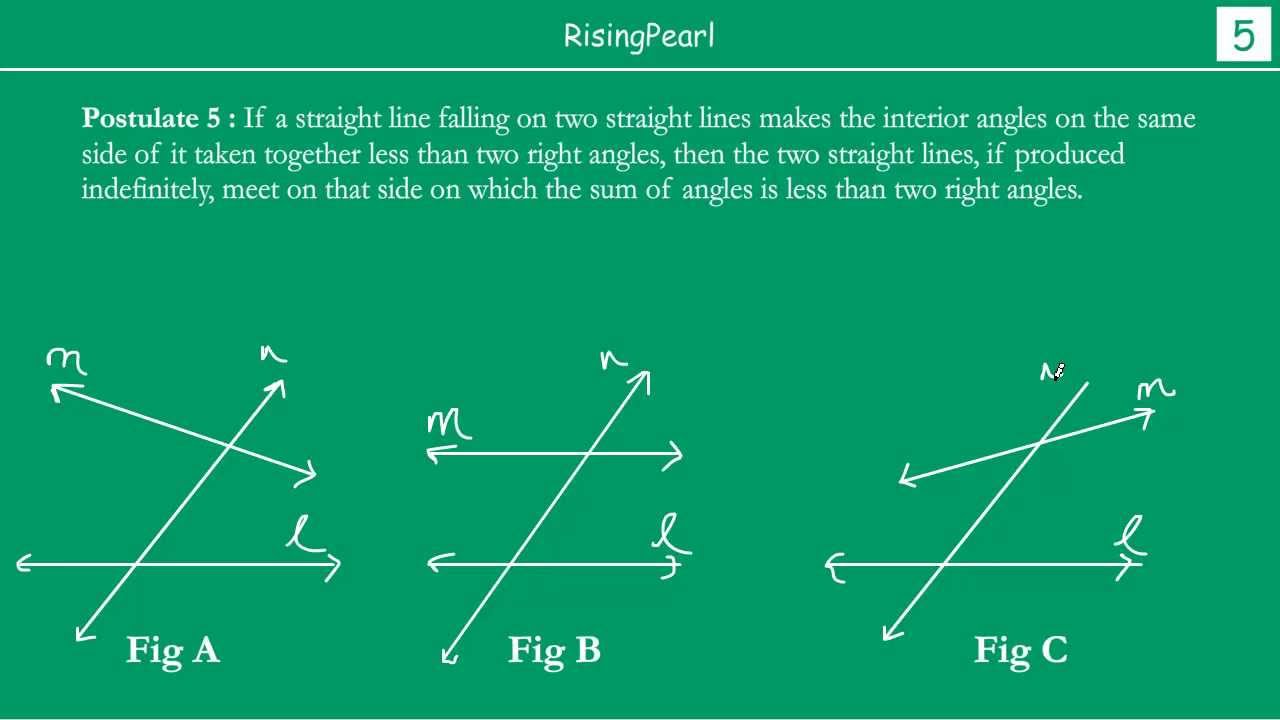
What does Euclid's 5th postulate say?
Euclid's fifth postulate states that if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two right angles, then both straight lines, if produced indefinitely, will meet on the other side on which the sum of angles is less than two right angles.
What are the postulates of Euclidean geometry?
What are the five postulates of Euclid’s geometry?
- A straight line may be drawn from any point to another point.
- A terminated line can be produced indefinitely.
- A circle can be drawn with any centre and radius.
- All right angles are equal to each other.
What is the meaning of postulates?
Postulates are statements assumed to be true without any requirement of proof. They are built upon the knowledge that satisfies the reader (or listener) in terms of veracity.
How are postulates and Theorems similar?
Postulates and Theorems. A postulate is a statement that is assumed true without proof. A theorem is a true statement that can be proven. Listed below are six postulates and the theorems that can be proven from these postulates. Postulate 1: A line contains at least two points. Postulate 2: A plane contains at least three noncollinear points.
What is the Euclids third postulate?
If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines inevitably must intersect each other on that side if extended far enough.
What are the 5 Euclidean postulates?
The five postulates on which Euclid based his geometry are:To draw a straight line from any point to any point.To produce a finite straight line continuously in a straight line.To describe a circle with any center and distance.That all right angles are equal to one another.More items...
What is the 3rd postulate?
Postulate 3: Through any two points, there is exactly one line.
How many postulates are there in Euclid's geometry?
5Euclid has introduced the geometry fundamentals like geometric shapes and figures in his book elements and has stated 5 main axioms or postulates.
What are Euclidean postulates?
If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
What are the basic postulates of Euclidean geometry?
0:502:41The 5 Postulates of Euclidean Geometry - YouTubeYouTubeStart of suggested clipEnd of suggested clipOn a flat surface Euclidean geometry can be Illustrated on flat paper or a chalk. Board. Because itMoreOn a flat surface Euclidean geometry can be Illustrated on flat paper or a chalk. Board. Because it is based on a flat surface all of the following will be true the shortest distance between two
What is the first postulate of Euclid?
Euclid's postulates were : Postulate 1 : A straight line may be drawn from any one point to any other point. Postulate 2 :A terminated line can be produced indefinitely. Postulate 3 : A circle can be drawn with any centre and any radius. Postulate 4 : All right angles are equal to one another.
What does Euclid's second postulate mean?
The second postulate of Euclid. Let us give below one of the formulations of the second postulate [1] A finite straight line may be extended continuously in a straight line. Like any statement expressed in verbal form, it differs in ambiguity and admits numerous variants.
What is SAS ASA and SSS congruence postulates?
The congruency can also be tested by three postulates shown in the lesson: ASA (angle-side-angle), SAS (side-angle-side), and SSS (side-side-side). The first one claims that triangles are congruent if two angles and one side (between the angles) of one triangle are equal to two angles and one side of another triangle.
What is Euclid's 4 postulate?
All right angles are congruent or equal to one another. A right angle is an angle measuring 90 degrees. So, irrespective of the length of a right angle or its orientation all right angles are identical in form and coincide exactly when placed one on top of the other.
What is the another name of Euclid's fifth postulate?
The converse of the parallel postulate: If the sum of the two interior angles equals 180°, then the lines are parallel and will never intersect.
What are postulates give two examples?
Some examples of mathematical postulates are: A line grows infinitely. All right angles are equivalent. The intersection between two planes is a line.
What is Euclid's 4th postulate?
All right angles are congruent or equal to one another. A right angle is an angle measuring 90 degrees. So, irrespective of the length of a right angle or its orientation all right angles are identical in form and coincide exactly when placed one on top of the other.
How many types of postulates are there?
The five postulates of Euclidean Geometry define the basic rules governing the creation and extension of geometric figures with ruler and compass.
What is the fifth proposition of Euclid?
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
What is SAS ASA and SSS congruence postulates?
The congruency can also be tested by three postulates shown in the lesson: ASA (angle-side-angle), SAS (side-angle-side), and SSS (side-side-side). The first one claims that triangles are congruent if two angles and one side (between the angles) of one triangle are equal to two angles and one side of another triangle.
State the five postulates of Euclidean geometry?
Five common postulates of Euclidean geometry are: • You can draw a straight-line segment from any given point to others. • You can extend a straigh...
What are the uses of Euclidean geometry?
We use Euclidean geometry to design buildings, predict the location of moving objects, and survey land.
How Euclid contribute to geometry?
From a small set of axioms Euclid deduced the theorems of what is now known as Euclidean geometry. In addition, he also wrote works on conic sectio...
How does Euclid define a line?
When Euclid first formalized the geometry, he defined a general line as “breathless length” as a straight line is a line “that lies evenly with the...
What are Euclid's postulates?
1. A straight line segment can be drawn joining any two points. 2. Any straight line segment can be extended indefinitely in a straight line. 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. All right angles are congruent .
Which postulate did Euclid use?
Euclid himself used only the first four postulates (" absolute geometry ") for the first 28 propositions of the Elements , but was forced to invoke the parallel postulate on the 29th.
After each and every natural disasters, the villages and cities required new constructions
After each and every natural disasters, the villages and cities required new constructions.
A well known mathematician Euclid tried to overcome this problem with his geometrical techniques
A well known mathematician Euclid tried to overcome this problem with his geometrical techniques.
Suppose we consider two points M and N. Then, we can draw a line M N by joining them
Suppose we consider two points M and N. Then, we can draw a line M N by joining them.
Then, the axiom is considered as, given any two distinct points, there is a unique line that passes through these points
Then, the axiom is considered as, given any two distinct points, there is a unique line that passes through these points.
Here, one end of line is center and radius is the length of line segment
Here, one end of line is center and radius is the length of line segment.
Then, the two lines automatically must intersect each other on that side if extended far enough
Then, the two lines automatically must intersect each other on that side if extended far enough.
The third postulate states that, from any given line segment we can draw a circle
The third postulate states that, from any given line segment we can draw a circle.
How many postulates did Euclid give?
He gave five postulates for plane geometry known as Euclid’s Postulates and the geometry is known as Euclidean geometry. It was through his works, we have a collective source for learning geometry; it lays the foundation for geometry as we know now.
What were Euclid’s Five Postulates?
Before discussing Postulates in Euclidean geometry, let us discuss a few terms as listed by Euclid in his book 1 of the ‘Elements’. The postulated statements of these are:
How many books are in Euclid's Elements?
Euclid’s Elements is a mathematical and geometrical work consisting of 13 books written by ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt. Further, the ‘Elements’ was divided into thirteen books which popularized geometry all over the world. As a whole, these Elements is a collection of definitions, postulates (axioms), ...
What are Euclid's axioms?
The axioms or postulates are the assumptions which are obvious universal truths, they are not proved. Euclid has introduced the geometry fundamentals like geometric shapes and figures in his book elements and has stated 5 main axioms or postulates. Here, we are going to discuss the definition of euclidean geometry, its elements, ...
What is the difference between Euclid geometry and parallel geometry?
In Euclid geometry, for the given point and line, there is exactly a single line that passes through the given points in the same plane and it never intersects.
What are the seven axioms of Euclid?
Here are the seven axioms given by Euclid for geometry. Things which are equal to the same thing are equal to one another. If equals are added to equals, the wholes are equal. If equals are subtracted from equals, the remainders are equal. Things which coincide with one another are equal to one another.
How to find the three steps from solids to points?
Assume the three steps from solids to points as solids-surface-lines-points. In each step, one dimension is lost. A solid has 3 dimensions, the surface has 2, the line has 1 and point is dimensionless. A point is anything that has no part, a breadthless length is a line and the ends of a line point.
Which postulates did Euler use to explain the affine geometry?
Euler discussed a generalization of Euclidean geometry called affine geometry, which retains the fifth postulate unmodified while weakening postulates three and four in a way that eliminates the notions of angle (whence right triangles become meaningless) and of equality of length of line segments in general (w hence circles become meaningless) while retaining the notions of parallelism as an equivalence relation between lines, and equality of length of parallel line segments (so line segments continue to have a midpoint).
Which logic is used in Euclid's geometry?
Classical logic. Euclid frequently used the method of proof by contradiction, and therefore the traditional presentation of Euclidean geometry assumes classical logic , in which every proposition is either true or false, i.e., for any proposition P, the proposition "P or not P" is automatically true.
How does Euclid prove the congruence of two triangles?
For example, proposition I.4, side-angle-side congruence of triangles, is proved by moving one of the two triangles so that one of its sides coincides with the other triangle's equal side, and then proving that the other sides coincide as well. Some modern treatments add a sixth postulate, the rigidity of the triangle, which can be used as an alternative to superposition.
What is Euclidean geometry?
Euclidean geometry is a mathematical system attributed to Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions ( theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.
How many proofs of the fifth postulate were published?
Many tried in vain to prove the fifth postulate from the first four. By 1763, at least 28 different proofs had been published, but all were found incorrect.
Why is Euclidean unnecessary?
For more than two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry had been conceived.
What is the transitive property of Euclidean relation?
Things that are equal to the same thing are also equal to one another (the transitive property of a Euclidean relation ). If equals are added to equals, then the wholes are equal (Addition property of equality). If equals are subtracted from equals, then the differences are equal (subtraction property of equality).
