- There are three types of congruent transformations: reflection, translation, and rotations.
- Congruence transformations do not change the shape or size of the object.
- If one shape can be obtained from another by a sequence of congruence transformations, the shapes are congruent.
- Congruency between two shapes can be proved by a single congruence transformation or by a sequence of congruence transformations.
What is a congruent transformation?
Two objects are congruent if they’re the identical measurement and form. A congruence transformation is a transformation that does not change the dimensions or form of an object. There are three primary kinds of congruence transformations, and people are reflections (flips), rotations (turns), and translations (slides).
Which of the following is a congruence transformation?
Congruence transformations are transformations performed on an object that create a congruent object. There are three main types of congruence transformations: Translation (a slide) Rotation (a turn) Reflection (a flip)Jan 15, 2021.
Which are types of transformations preserve congruence?
Two objects are congruent if they are the same size and shape. A congruence transformation is a transformation that doesn't change the size or shape of an object. There are three main types of congruence transformations, and those are reflections (flips), rotations (turns), and translations (slides). Click to see full answer.
Is reflecting a congruence transformation?
In mathematics, this is called a reflection, and it’s an example of a congruence transformation. We say that two objects are congruent if they have the same shape and size. We say that two objects are congruent if they have the same shape and size.
What are the 3 congruent transformations?
Congruence transformations Using three forms of transformations, Rotations, Reflections and Translations, we can create congruent shapes. In fact all pairs of congruent shapes can be matched to each other using a series or one or more of these three transformations.
How do you find congruence transformations?
3:408:50Geometry 4.7 Congruence Transformations - YouTubeYouTubeStart of suggested clipEnd of suggested clipWhenever you make a transformation. You can verify that it is a congruence transformation to verifyMoreWhenever you make a transformation. You can verify that it is a congruence transformation to verify that you need to make sure that each of the shapes is the same shape and same size.
What are the 4 types of congruence?
Different rules of congruency are as follows.SSS (Side-Side-Side)SAS (Side-Angle-Side)ASA (Angle-Side-Angle)AAS (Angle-Angle-Side)RHS (Right angle-Hypotenuse-Side)
How many transformations are congruent?
Two figures are congruent if you can translate, rotate, and/or reflect one shape to get the other. Congruence and Transformations Using congruence transformations, including translation, reflection, and rotation.
Which transformation is not congruent?
non-rigid transformationsRigid transformations are transformations that preserve the shape and size of the geometric figure. Only position or orientation may change, so the preimage and image are congruent. In non-rigid transformations, the preimage and image are not congruent.
What are congruent shapes examples?
If two figures have the same shape and the same size, then they are said to be congruent figures. For example, rectangle ABCD and rectangle PQRS are congruent rectangles as they have the same shape and the same size. Side AB and side PQ are in the same relative position in each of the figures.
What are the 5 rules of congruence?
Two triangles are congruent if they satisfy the 5 conditions of congruence. They are side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), angle-angle-side (AAS) and right angle-hypotenuse-side (RHS).
What are the 3 properties of congruence?
The three properties of congruence are the reflexive property, the symmetric property, and the transitive property. Reflexive property says that any angle A is congruent to angle A. Symmetric property says that if angle A is congruent to angle B, then angle B is congruent to angle A.
What are the 4 ways to prove triangles are congruent?
These four criteria used to test triangle congruence include: Side – Side – Side (SSS), Side – Angle – Side (SAS), Angle – Side – Angle (ASA), and Angle – Angle – Side (AAS). There are more ways to prove the congruency of triangles, but in this lesson, we will restrict ourselves to these postulates only.
What are the 5 transformations?
These are Transformations:RotationTurn!ReflectionFlip!TranslationSlide!
What are the 4 transformations in maths?
There are 4 types of transformation: translation, rotation, reflection, and enlargement. You need to be able to perform each transformation as well as identify which transformations have been performed.
What are the different types of transformations?
There are four main types of transformations: translation, rotation, reflection and dilation.
How do you determine if a shape is congruent?
Congruent shapesThe three sides are equal (SSS: side, side, side)Two angles are the same and a corresponding side is the same (ASA: angle, side, angle)Two sides are equal and the angle between the two sides is equal (SAS: side, angle, side)More items...
Which transformation S can be used to map △ RST onto △ VWX?
Which tranformation(s) can be used to map RST onto VWX? d. rotation, then translation.
What are the congruence theorems?
In simple words, if all the three sides of one triangle are equal to all the three sides of another triangle, then both the triangles are congruent to each other.
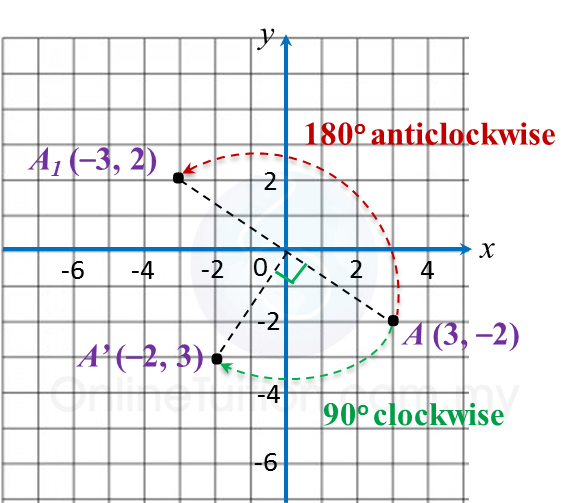
Is rotating a congruence transformation?
Since the size and shape of figures are not affected when a figure is rotated, we say rotations are congruence transformations.
What are congruence transformations?
Congruence transformations are transformations which when performed on an object produce congruent objects.
What are the 3 types of congruence transformations?
Rotation Reflection Translation
How can you visually identify a congruence transformation?
A congruence transformation does not change the shape or size of the object
Give real three life examples of congruence transformations
Sliding a paper on a tabletop (translation) A number rotating in a roulette wheel (rotation) Reflection on a mirror (reflection)
What are congruence transformations rules?
A congruence transformation should not change the shape or size of the object when applied to the object. If one object can be moved and placed exa...
Why is dilation not a congruence transformation?
Because it changes the size of the object which breaks the rules that define a congruent transformation.
What is a congruent transformation?
Congruence transformations are transformations performed on an object that create a congruent object. There are three main types of congruence transformations: Translation (a slide) Rotation (a turn) Reflection (a flip) Congruence transformations happen all the time in our daily lives.
Why are congruence transformations interesting?
Congruence transformations are interesting, because various combinations of transformations are equivalent to various other combinations of transformations. For instance, the reflections in parallel lines theorem states that if we reflect an image over two parallel lines, it is the same as translating that image.
How to define congruent objects?
This is another way to define congruent objects. That is, two objects are congruent if we can move one of the objects, without changing its shape or size, in such a way that it fits exactly over the other image. We call these movements congruence transformations. Congruence transformations are transformations performed on an object ...
What is the definition of congruent?
Two objects are congruent if they are the same size and shape. We can also define objects as congruent if we can move one object to obtain the other object through a congruence transformation, one that doesn't change the size or shape of an object. There are three main types of congruence transformations: reflections (flips), rotations (turns), and translations (slides). These congruence transformations can be used to obtain congruent shapes or to verify that two shapes are congruent.
What is the result of the reflections in intersecting lines theorem?
The reflections in intersecting lines theorem states that if two lines intersect one another, and we reflect a shape over one and then the other, the result is the same as a rotation of the original shape.
How do you know if two objects are congruent?
We say that two objects are congruent if they have the same shape and size. For instance, our reflections in a mirror have the same shape and size as we do, so we would say that we are congruent to our reflection in a mirror.
What is the reflection in parallel lines theorem?
The reflections in parallel lines theorem states that if two lines are parallel and you reflect a shape over one and then the other, the result is the same as a translation of the original shape.
How to translate a figure in coordinate plane?
To translate or reflect or rotate a figure in the coordinate plane, we have to transform each of its vertices. Then, we have to connect the vertices to form the image.
How many vertices does a triangle have?
A triangle has the vertices (3, 4), (5, 4) and (5, 2). Apply the indicated series of transformations to the triangle. Each transformation is applied to the image of the previous transformation, not the original figure. Label each image with the letter of the transformation applied.
How many units to add to each y coordinate?
Since there is a translation of 4 units up, we have to add 4 to each y-coordinate. That is,