
CHARACTERISTICS OF QUADRATIC FUNCTIONS
- Axis of symmetry
- x and y-intercepts
- Zeroes
- vertex
- Point symmetric to y-intercept
What makes it a quadratic function?
quadratic function, a quadratic polynomial, a polynomial of degree 2, or simply a quadratic, is a polynomial function with one or more variables in which the highest-degree term is of the second degree. For example, a quadratic function in three variables x, y, and z contains exclusively terms x^2,y^2,z^2, xy, xz, yz, x, y, z, and a constant:
What are the two forms of a quadratic function?
- General form: we should all know this one. f ( x) = a x 2 + b x + c. ...
- Vertex form: f ( x) = a ( x − h) 2 + k. ...
- Intercept form: f ( x) = a ( x − b) ( x − c). My favourite form; the factorised version of the equation. This one here
What does a quadratic function look like?
The shape of a quadratic is called a parabola . This shape looks like a u (or n) when we graph the quadratic function. If the quadratic function has the form f (x) = ax 2 + bx + c, then the shape depends on the sign of a: For a > 0: the parabola is u-shaped, since it opens upward (it is convex or concave up)
How do you find a quadratic function?
Method 2 Method 2 of 2: Completing the Square
- Write down the equation. Completing the square is another way to find the vertex of a quadratic equation.
- Dividing each term by 1 would not change anything. Dividing each term by 0, however, will change everything.
- Move the constant term to the right side of the equation. ...
- Complete the square on the left side of the equation.
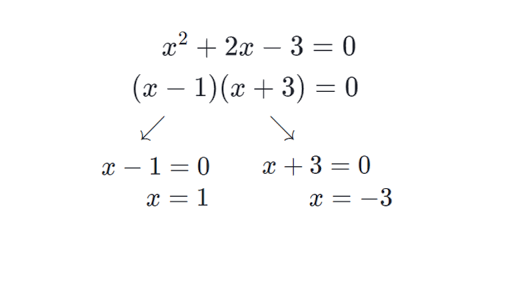
What are the 5 key features of a quadratic graph?
There are many key features in a quadratic graph such as the zeroes (x-intercepts, also known as the roots), y-intercept, axis of symmetry, and the vertex.
What are the key concepts of quadratic equations?
A quadratic equation can be expressed in the general form of ax2+bx+c=0, where a, b and c are numerical coefficients or constants, and the value of x is variable. One fundamental rule of a quadratic equation is that the value of the first constant never can be zero.
How do you identify the key features of a function?
Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.
What are the properties of quadratic equation?
properties of quadratic equationIt has in C two roots (which may be equal), since the complex numbers. form an algebraically closed field containing the coefficients.• The sum of the roots is equal to −ba , i.e. −p .• The product. of the roots is equal to ca , i.e. q .
What is the concept of quadratic function?
A quadratic function is a function whose rule may be written in the form f(x) = ax2 + bx + c where a, b, and c are real numbers and a is not zero. The graph of a quadratic function is a parabola which opens up if. a > 0 and opens down if a < 0.
How do you identify a quadratic equation?
0:031:55Identifying Quadratic Equations - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe quadratic equations a quadratic equation is an equation where you have X to the 2nd power andMoreThe quadratic equations a quadratic equation is an equation where you have X to the 2nd power and that's your highest power of X. So y equals x squared would be the most basic quadratic.
What are the key features?
Key Features means the document describing the important characteristics of the Plan to which your application relates, including its aims and associated risks.
What are the key concepts of functions?
A function is tied to a specific rule, formula, or computation and requires the completion of specific computations and/or steps. A function is a generalized input-output process that defines a mapping of a set of input values to a set of output values. A student must perform or imagine each action.
How do you interpret key features of functions and graphs?
0:1022:14Identify Key Features of Graphs - YouTubeYouTubeStart of suggested clipEnd of suggested clipX-intercept so this is the point where a graph goes through the x-axis. So there can be more thanMoreX-intercept so this is the point where a graph goes through the x-axis. So there can be more than one x-intercept. So it's at every single point where your graph goes through the x-axis.
How do you find the key features of a parabola?
0:026:35Identifying Key Features of a Parabola - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe top part or the bottom part of the graph this is known as your vertex. So wherever the graphMoreThe top part or the bottom part of the graph this is known as your vertex. So wherever the graph curves. This is going to be your vertex. Your vertex should always be written as an ordered pair.
What are the 5 examples of quadratic equation?
Examples of the standard form of a quadratic equation (ax² + bx + c = 0) include:6x² + 11x - 35 = 0.2x² - 4x - 2 = 0.-4x² - 7x +12 = 0.20x² -15x - 10 = 0.x² -x - 3 = 0.5x² - 2x - 9 = 0.3x² + 4x + 2 = 0.-x² +6x + 18 = 0.
Does every quadratic function have a vertex?
The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function.
What are 4 examples of quadratic equation?
Examples include:2x² - 64 = 0.x² - 16 = 0.9x² + 49 = 0.-2x² - 4 = 0.4x² + 81 = 0.-x² - 9 = 0.3x² - 36 = 0.6x² + 144 = 0.
What are the four methods in solving quadratic equations?
The four methods of solving a quadratic equation are factoring, using the square roots, completing the square and the quadratic formula.
What are the forms of quadratic equations?
The 3 Forms of Quadratic EquationsStandard Form: y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c.Factored Form: y = a ( x − r 1 ) ( x − r 2 ) y=a(x-r_1)(x-r_2) y=a(x−r1)(x−r2)Vertex Form: y = a ( x − h ) 2 + k y=a(x-h)^2+k y=a(x−h)2+k.
What pre knowledge concepts would a Grade 11 learner need to know before learning quadratic equations?
Here are three prerequisite topics are key to understanding quadratic equations: Principles of Graphing. Basic Solving Skills. Factoring.
What is the point symmetric to y intercept?
The point symmetric to y intercept will have the same horizontal distance from the axis of symmetry.
How to get zeros of a quadratic function?
We can get the zeroes of a quadratic function by applying y = 0. Zeroes of a quadratic function and x-intercepts are same.
What is the point at which the parabola cuts the x-axis?
The point at which the parabola cuts the x-axis is known as x-intercept.To find x-intercept we have to put y = 0.
Why is the parabola open upward?
Because a > 0, the parabola is open upward.
Can the y intercept be reflected across the axis of symmetry?
The y-intercept (and other points) can be reflected across the axis of symmetry to find other points on the graph of the function.
Do quadratic functions have characteristics?
Each quadratic functions will have some characteristics.
