The most common form of explicit proof in highschool geometry is a two column proof consists of five parts: the given, the proposition, the statement column, the reason column, and the diagram(if one is given). What is a geometry proof? Geometric
Geometry
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.
What is a cuemath mini lesson?
What is an equilateral triangle?
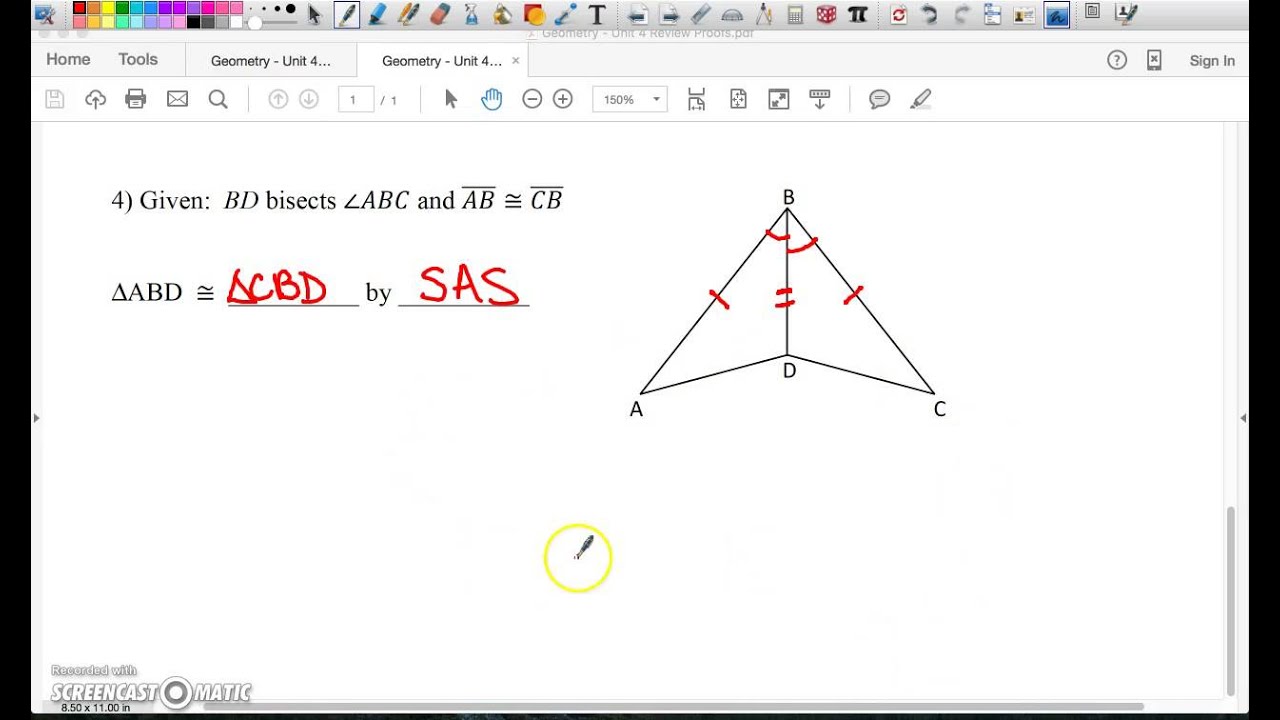
What is 2.AD 2. A D?
What is geometric proof?
What is the axiom for XY?
Can an equilateral triangle be constructed on any segment?
See 3 more
About this website

What are the different types of proofs in geometry?
Paragraph proofs and geometric proofs are the two main types of proofs in geometry. Among these two, two-column proofs are widely used as they are...
How do you solve proofs in geometry?
Write down the given information in a summarized manner. Draw a figure. Decide on the outline to proceed. Write down the statements and reasons by...
What are the parts to a geometry proof?
The given information, things to prove, the figures, and statements with their reasons are the main parts of the geometry proof. The if-then struct...
Proofs and Postulates - Math Plane
Proofs and Postulates - Math Plane
What is geometric proof?
We need a geometric proof. A geometric proof is a method of determining whether a statement is true or false with the use of logic, facts and deductions. A proof is kind of like a series of directions from one place to another.
What does it mean to enroll in a course?
Enrolling in a course lets you earn progress by passing quizzes and exams.
What is a two column proof?
A two-column proof has - wait for it - two columns. The column on the left is a list of statements. These are things we know are true. On the right, we have a list of reasons. This is the 'why' for each statement.
Why do you need to write a proof?
In a proof, what's given can be a big deal. When you start writing your proof, the only reason why that you need for these statements is that they're given. If it said, 'Runners live, on average, 150 years longer than non-runners,' well, that's crazy talk, but it's a given statement, so it's valid in your proof.
Is triangle XYB congruent to triangle XZB?
Now triangle XYB is congruent to triangle XZB. That's the SSS postulate. Great! Are we done? Check the problem. We wanted to find out if those two angles are congruent. So, we need one more step. Be careful not to get to that big moment, like finding that two triangles are congruent, and stopping.
Is XY congruent to XZ?
So, we have a triangle, XYZ. We know XY is congruent to XZ. That's one of our given statements. So, let's add hash marks to remember that. There's a point B on YZ - let's add that. And there's a line from X to B. That bisects YZ. If it bisects YZ, then YB and BZ are congruent. Let's add hash marks to remember that.
Can proofs be written in paragraph form?
These proofs can be written as a two-column chart or in paragraph form. You see the two-column kind more often. This is a neat, orderly way to walk through the steps. We're more likely to skip a step in the paragraph style, though there's nothing inherently wrong with that format.
How to find the exterior angle of a triangle?
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles and the value is greater than either non-adjacent interior angle.
What happens when you get thorough with the geometry proofs list?
Once they get thorough with the geometry proofs list, they would get an intuition for how different structures act and interact and what strategies might be best to apply.. this way they won't even find geometry hard, and will be able to solve the complete list of geometry proofs.
What does it mean when a triangle is isosceles?
Says that “If a triangle is isosceles, then its BASE ANGLES are congruent.” This applies to the above point that you have already learned.
What is geometry proof?
Geometry proofs are what math actually is. To put it simply- they're the explanation, and everything else follows from them. This means they're the most important part of the whole field by a very large measure, but they're generally going to be more difficult than anything else.
Why are geometry proofs different from solving problems?
They're inherently different from solving problems because you already know the result and are solving for it . All kids need to do is manipulate the logic and structures after understanding how to solve these geometry proofs.
What is a tangent drop in a circle?
A tangent dropped to a circle, is perpendicular to the radius made at the point of tangency. Tangent segments from a single point to a circle at different points are equal. An angle inscribed in a semi-circle or half-circle is a right angle. This was the important geometry proofs list.
What does a parallel line mean in a proof?
3. Parallel Lines can be a lifesaver. This is an old trick that you would be familiar with as well. Any parallel lines in the proof’s diagram mean that you would use one of the parallel-line theorems. Pass on this wisdom to help your children solve geometry proofs given in the geometry proofs list. 4.
What is a Proof in Geometry?
Before beginning geometry proofs, review key concepts related to the topic.
How to Describe the Main Parts of a Proof
A geometric proof uses the given statement, facts, deduction, logic, and a figure from which the given statement is proven. All of these arguments, together with their reasons, are written down, and then the answer is given.
Geometry Proofs: Paragraph Proofs vs. Two-Column Proofs
Two types of proof that are widely used in geometry are paragraph proofs and two-column proofs.
How to Write Geometry Proofs
Let's look at an example of a two-column proof. Though it is a basic example, it will give an idea of how to proceed with a two-column proof.
Answer
The most common form of explicit proof in high school geometry is a two column proof consists of five parts: the given, the proposition, the statement column, the reason column, and the diagram.
Answer
Proofs contain given information and a statement to be proven. You use deductive reasoning to create an argument with justification of steps using theorems, postulates, and definitions. Then you arrive at a conclusion.
What is a cuemath mini lesson?
The mini-lesson targeted the fascinating concept of Geometric Proofs. The math journey around proofs starts with the statements and basic results that a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
What is an equilateral triangle?
Solution. An equilateral triangle is a triangle in which all three sides are equal. Suppose that you have a segment XY X Y: You want to construct an equilateral triangle on XY X Y. Euclid’s third postulate says that a circle can be constructed with any center and any radius.
What is 2.AD 2. A D?
2.AD 2. A D is the angle bisector of ∠ ∠ A A
What is geometric proof?
A geometric proof is a deduction reached using known facts such as axioms, postulates, lemmas, etc. with a series of logical statements. While proving any geometric proof statements are listed with the supporting reasons.
What is the axiom for XY?
Clearly, XY =XZ X Y = X Z (radii of the same circle) and XY = Y Z X Y = Y Z (radii of the same circle). Also, one of Euclid’s axioms says that things that are equal to the same thing are equal to one another. Thus,
Can an equilateral triangle be constructed on any segment?
Thus, we have proved that an equilateral triangle can be constructed on any segment, and we have shown how to carry out that construction.