
...
| PROPERTIES OF INEQUALITY | |
|---|---|
| Anti reflexive Property | For all real numbers x , x≮x and x≯x |
| Addition Property | For all real numbers x,y, and z , if x<y then x+z<y+z . |
How do the properties help solve equations and inequalities?
Solving multi-step inequalities is very similar to solving equations—what you do to one side you need to do to the other side in order to maintain the “balance” of the inequality. The Properties of Inequality can help you understand how to add, subtract, multiply, or divide within an inequality.
What are some examples of properties of equality?
Three Properties of Equality
- The reflexive property states that any real number, a, is equal to itself. That is, a = a .
- The symmetric property states that for any real numbers, a and b, if a = b then b = a .
- The transitive property states that for any real numbers, a, b, and c, if a = b and b = c, then a = c .
What are the properties of equality and inequality?
What are the properties of equality and inequality?
- The Reflexive Property. a =a.
- The Symmetric Property. If a=b, then b=a.
- The Transitive Property. If a=b and b=c, then a=c.
- The Substitution Property. If a=b, then a can be substituted for b in any equation.
- The Addition and Subtraction Properties.
- The Multiplication Properties.
- The Division Properties.
- The Square Roots Property*
How do you use inequalities in real life?
- Some people are more intelligent than me.
- Some people are more good looking than me.
- Some people make more money than me.
- Some people have better degrees from better schools than me.
- Some people have more power than me.
- Some people have more talent than me.
- Some people work harder than me.
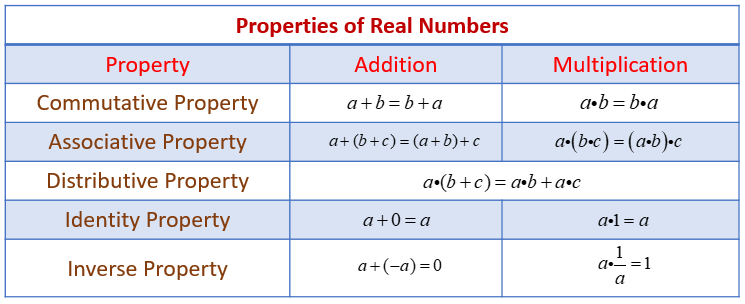
What are the 4 properties of inequality?
Properties of inequalityAddition property: If x < y, then x + z < y + z. ... Subtraction property: If x < y, then x − z < y − z. ... Multiplication property:z > 0. If x < y, and z > 0 then x × z < y × z. ... z < 0. If x < y, and z < 0 then x × z > y × z. ... Division property:It works exactly the same way as multiplication.z > 0.More items...
What is property of inequality?
Transitive Properties of Inequality: If a < b and b < c, then a < c. If a > b and b > c, then a > c.
What are the 6 properties of equality?
The Reflexive Property. a =a.The Symmetric Property. If a=b, then b=a.The Transitive Property. If a=b and b=c, then a=c.The Substitution Property. If a=b, then a can be substituted for b in any equation.The Addition and Subtraction Properties. ... The Multiplication Properties. ... The Division Properties. ... The Square Roots Property*
What are the four properties of equality in math?
The addition, subtraction, multiplication, and division properties of equality help to solve algebraic equations involving real numbers. The reflexive, symmetric, and transitive properties of equality together define the equivalence relation.
What is properties of equality?
3. Transitive property of equality: Two quantities that are equal to the same thing are equal to each other. Example: If x = 10 and 10 = y, then x = y.
What types of inequality are there?
There are five systems or types of social inequality: wealth inequality, treatment and responsibility inequality, political inequality, life inequality, and membership inequality.
How many properties of equalities are there?
PROPERTIES OF EQUALITYReflexive PropertyFor all real numbers x , x=x . A number equals itself.These three properties define an equivalence relationSymmetric PropertyFor all real numbers x and y , if x=y , then y=x . Order of equality does not matter.7 more rows
What is associative property of equality?
The Associative Property is simply a mathematical way of stating that if we are adding three numbers, the order in which we add them does not matter. Similarly, if we are multiplying three numbers together, the order in which we multiply them does not matter. EXAMPLE 1. (3+4)+6=3+(4+6) (7)+6=3+(10)
What are the 3 properties of addition?
Properties of additionCommutative property of addition: Changing the order of addends does not change the sum. ... Associative property of addition: Changing the grouping of addends does not change the sum. ... Identity property of addition: The sum of 0 and any number is that number.
What are the four properties?
Number Properties – Definition with ExamplesCommutative Property.Associative Property.Identity Property.Distributive Property.
What is distributive property of equality?
The distributive property states that the product of an expression and a sum is equal to the sum of the products of the expression and each term in the sum.
What is the commutative property of equality?
Commutative Property For addition, the rule is "a + b = b + a"; in numbers, this means 2 + 3 = 3 + 2. For multiplication, the rule is "ab = ba"; in numbers, this means 2×3 = 3×2.
Q.1. What are the properties of inequality?
Ans: The following are the properties of linear inequalities: i. The sign of a positive term becomes negative when it is transferred from one side...
Q.2. What are the basic properties of the addition of inequality?
Ans: According to the addition property of linear inequality, adding the same number to each side of the inequality results in an equivalent inequa...
Q.3. What is the distributive property of inequality?
Ans: Parentheses have a role in the inequalities you'll see in this concept. The distributive property can be used to simplify an equation containi...
Properties of addition and subtraction
When we add z to both sides of the inequality, we are simply moving the whole inequality, so the inequality remains the same:
Properties of multiplication and division
When we multiply both x and y by a positive number, the inequality remains the same.
Transitive property
When we relate inequalities in order, we can skip the inequality in the middle.
Antisymmetric property
The values x and y cannot be swapped if we keep the same inequality sign.
Properties of Linear Inequalities
An inequation is said to be linear if and only if the exponent of each variable in it is one (or each variable occurs in first degree only) and there is no term involving the variables’ product. The following are the properties of linear inequalities:
Addition Property of Inequality Definition
According to the addition property of linear inequality, adding the same number to each side of the inequality results in an equivalent inequality, i.e., the inequality symbol remains the same.
Subtraction Property of Inequality Definition
According to the linear inequality subtraction property, removing the same number from either side generates an identical inequality, i.e., the inequality symbol remains the same.
Multiplication Property of Inequality Definition
According to the linear inequality multiplication property, multiplying both sides of an inequality by a positive number always results in an equivalent inequality, i.e., the inequality symbol remains the same.
Division Property of Inequality Definition
According to the division property of linear inequality, dividing both sides of an inequality with a positive number results in an equivalent inequality, i.e., the inequality symbol remains the same.
Comparison Property of Inequality
Comparison property in mathematics in inequality is a relation that compares two numbers or other mathematical expressions in a non-equal way. It’s mostly used to compare two numbers on a number line based on their size.
Summary
In this article, we learnt about properties of linear inequalities, addition property of inequality definition, subtraction property of inequality definition, multiplication property of inequality definition, division property of inequality definition, transitive property of inequality, comparison property of inequality, solved examples on properties of inequalities, and FAQs on properties of inequalities..
Formal Definition of Inequalities
There are formal definitions of the inequality relations > , < ,≥,≤ in terms of the familiar notion of equality. We say a is less than b, written a < b if and only if there is a positive number c such that a + c = b. Recall that zero is not a positive number, so this cannot hold if a = b.
The Trichotomy Property and the Transitive Properties of Inequality
Trichotomy Property: For any two real numbers a and b, exactly one of the following is true: a < b, a = b, a > b .
Properties of Multiplication and Division
Before examining the multiplication and division properties of inequality, note the following: Inequality Properties of Opposites
How to determine the direction of an inequality?
Use the number line to determine the direction of the inequality. Multiply each side by -1. Use the number line to determine the direction of the inequality. Notice that when you multiply (or divide) both sides of an inequality by a negative number, you must reverse the inequality symbol.
Can you subtraction property of inequality?
Subtraction Property of Inequality. Same number can be subtracted from each side of an inequality , and the statement will still be true. Because there can be an infinite number of solutions to an inequality, it is not possible to check all the solutions.
What Are Properties of Equality?
Properties of equality are facts about any two or more quantities related with an equal sign.
How Are Properties of Equality Used?
Properties of equality are useful in a variety of mathematical contexts.
Examples
This section covers common problems using properties of equality and their step-by-step solutions.

Properties of Addition and Subtraction
Properties of Multiplication and Division
- When we multiply both x and yby a positive number, the inequality remains the same. However, when we multiply both x and yby a negative number, the inequality flips. x>y becomes x<ywhen multiplying by -2 But the inequality remains the same when multiplying by 2 These are the general rules: 1. If x<y and z is positive, then xz<yz 2. If x<y and z is ...
Transitive Property
- When we relate inequalities in order, we can skip the inequality in the middle. If we have x<y and y<z, then x<z. Similarly, if we have x>y and y>z, then x>z.
Antisymmetric Property
- The values x and ycannot be swapped if we keep the same inequality sign. 1. If we have x>y, this is different than y>x. Then, we have y≯x 2. If we have x<y, this is different than y<x. Then, we have y≮x If we swap the x and yvalues, we must make sure to change the inequality sign: 1. If x>y, then, y<x 2. If x<y, then, y>x
See Also
- Interested in learning more about inequalities? Take a look at these pages: 1. How to Solve Linear Inequalities? 2. Examples of Inequalities 3. Examples of Linear Inequalities