Features of a Right Triangle
- The right angle is always the largest angle in a right triangle.
- The hypotenuse, the side opposite the right angle, is the longest side.
- There can’t be any obtuse angles in a right triangle.
What angles make a right triangle?
Key Terms
- legs: The sides adjacent to the right angle in a right triangle.
- right triangle: A 3 3 -sided shape where one angle has a value of 90 90 degrees
- hypotenuse: The side opposite the right angle of a triangle, and the longest side of a right triangle.
What is a real life example of a right triangle?
While teaching various types of triangles, when you provide the right triangle concept, you can provide examples of stairs and stairs. The reason is that these stairs and stairs are built on the right triangle triangle concept. When you put the stairs on the wall, the stairs make the right corner triangle with the wall.
How many right angles are there in a right triangle?
In the Euclidean plane, triangles can have at most one right angle, because 2 right angle turns put you on course parallel to the first side, which, by the parallel postulate, will never meet. It would take at least two more turns to get back to the original side, but a triangle has only three angles.
What are the characteristics of right triangles?
Characteristics of the right triangle They are polygons that have three sides. They are formed by three segments. They all have a right angle of ninety degrees. The two angles that are not right will always be acute angles. The right angle is made up of the two shorter side. They can be isosceles or scalene.

What must a right triangle have?
A right triangle is a triangle that has one angle whose measure is 90°. A right triangle CANNOT have two 90º angles. This is because the angles of a triangle must add up to 180°. With one angle measuring 90°, the other two angles in the right triangle must add up to 90°.
What are the 3 sides of a right triangle?
In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle. We use special words to describe the sides of right triangles.
What makes a triangle a right triangle?
The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90°. The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.
What triangle has a right angle?
A right angled triangle is a triangle with one of the angles as 90 degrees. A 90-degree angle is called a right angle, and hence the triangle with a right angle is called a right triangle. In this triangle, the relationship between the various sides can be easily understood with the help of the Pythagoras rule.
What are the 4 main parts to a right triangle?
These sides are the hypotenuse, the opposite side, and adjacent side. Using the figure above, the hypotenuse is side c, the opposite side is side a, and the adjacent side is side b. Here are the sides of a general right triangle labeled in the coordinate lane.
Can triangles have 3 right angles?
No, a triangle cannot have 3 right angles. Since the sum of the angles in a triangle is 180 degrees.
How do you know if it makes a right triangle?
The converse of the Pythagorean Theorem is: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. That is, in ΔABC, if c2=a2+b2 then ∠C is a right triangle, ΔPQR being the right angle.
How do you identify a right angle?
To test if an angle is right angle, place a protractor over one line of the angle and read the number that is in line with the other line of the angle. If the angle is 90 degrees, then it is a right angle.
What angles does a triangle have?
A triangle has three angles. The sum of the measures of the angles is always 180° in a triangle. We have different types of triangles. A triangle is classified by its angles and by the number of congruent sides.
Do right triangles have two equal sides?
An isosceles right triangle has the characteristic of both the isosceles and the right triangles. It has two equal sides, two equal angles, and one right angle.
How many angles does a right triangle have?
Explanation: The sum of the angles in a triangle is 180. A right triangle has one angle of 90. Thus, the sum of the other two angles will be 90.
How do you find the 3rd side of a triangle?
Different Ways to Find the Third Side of a Triangle For a right triangle, use the Pythagorean Theorem. For an isosceles triangle, use the area formula for an isosceles. If you know some of the angles and other side lengths, use the law of cosines or the law of sines.
Does a right triangle have 3 equal sides?
A right triangle can be scalene (having all three sides of different length) or isosceles (having exactly two sides of equal length). It can never be an equilateral triangle.
Can a right triangle have two equal sides?
A right triangle can also be an isosceles triangle which means that it has two sides and two angles equal. A right isosceles triangle has a 90° ang...
Can 8 cm, 15 cm, and 17 cm form three sides of a right triangle?
We can check if 8 cm, 15 cm, and 17 cm form three sides of a right triangle using the pythagorean theorem. H (Hypotenuse)2 = P (Perpendicular heigh...
What are the 3 sides of the right triangle called?
The base, perpendicular height, and hypotenuse are the three sides of a right triangle.
What is the pythagorean formula for a right-angled triangle?
The Pythagoras theorem states the following formula for a right triangle:H (Hypotenuse)2 = P (Perpendicular height)2 + B (Base)2
What are Right Angled Triangles?
Right-angled triangles are those triangles in which one angle is 90 degrees. Since one angle is 90°, the sum of the other two angles will be 90°.
How to Find the Missing Side of any Right Angled Triangle?
For a right-angled triangle, trigonometric functions or the Pythagoras theorem can be used to find its missing sides. If two sides are given, the P...
Can a Triangle have Two Right Angles? Explain.
No, a triangle can never have 2 right angles. A triangle has exactly 3 sides and the sum of interior angles sum up to 180°. So, if a triangle has t...
What is the sum of all the interior angles of the right triangle?
For any triangle, the sum of all the interior angles is equal to 180 degrees.
What are the three sides of the right triangle?
The three sides of a right triangle are base, perpendicular and hypotenuse. What is the formula for a right-angled triangle? We can use the Pytha...
What is a right triangle?
Right Triangle Definition. All triangles have interior angles adding to 180° 180 °. When one of those interior angles measures 90° 90 ° , it is a right angle and the triangle is a right triangle. In drawing right triangles, the interior 90° 90 ° angle is indicated with a little square □ in the vertex. The term "right" triangle may mislead you ...
How many angles does a right triangle have?
A right triangle must have one interior angle of exactly 90° 90 °. It can be scalene or isosceles but never equilateral.
What is the right triangle altitude theorem?
The right triangle altitude theorem tells us that the altitude of a right triangle drawn to the hypotenuse c c forms two similar right triangles that are also similar to the original right triangle.
What is the Pythagorean theorem?
You also know what the Pythagorean Theorem is ( a2 + b2 = c2 a 2 + b 2 = c 2) and how to prove it, and what the right triangle altitude theorem is (the altitude of a right triangle drawn to the hypotenuse c c forms two similar right triangles that are also similar to the original right triangle) and how to prove it.
How to tell if a new triangle is similar to the original triangle?
You can prove this by seeing that new triangle's ∠ADC ∠ A D C = original triangle's ∠AC B ∠ A C B, while new triangle's ∠C AD ∠ C A D = original triangle's ∠C AB ∠ C A B.
What is 9 square units + 16 square units?
Think: what is 9 square units + 16 square units? It is 25 square units, the area of c2 c 2 .
Is the vertex of a right triangle a right angle?
We already know the square vertex of the right triangle is a right angle. Opposite it is the triangle's hypotenuse, the longest of the three sides, usually labeled c c.
How to find area of a right triangle?
In a right triangle, if one leg is taken as the base then the other is height, so the area of a right triangle is one half the product of the two legs. As a formula the area T is.
What is the name of the triangle with the lengths of all three sides?
If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple .
What triangles can be used to evaluate trigonometric functions?
The values of the trigonometric functions can be evaluated exactly for certain angles using right triangles with special angles. These include the 30-60-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/6, and the 45-45-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/4.
How to find the altitude of a triangle?
If an altitude is drawn from the vertex with the right angle to the hypotenuse then the triangle is divided into two smaller triangles which are both similar to the original and therefore similar to each other. From this: 1 The altitude to the hypotenuse is the geometric mean ( mean proportional) of the two segments of the hypotenuse. 2 Each leg of the triangle is the mean proportional of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.
How many smaller triangles are there in a triangle?
If an altitude is drawn from the vertex with the right angle to the hypotenuse then the triangle is divided into two smaller triangles which are both similar to the original and therefore similar to each other. From this:
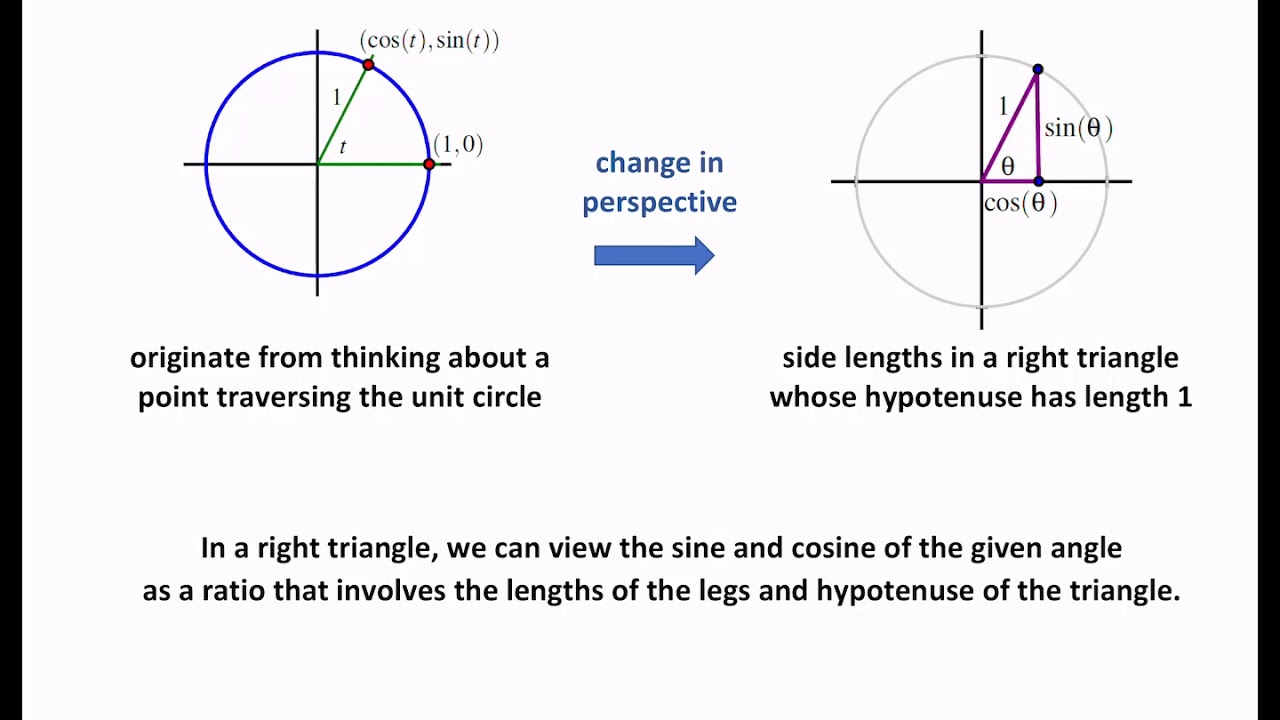
What are trigonometric functions?
The trigonometric functions for acute angles can be defined as ratios of the sides of a right triangle. For a given angle, a right triangle may be constructed with this angle, and the sides labeled opposite, adjacent and hypotenuse with reference to this angle according to the definitions above. These ratios of the sides do not depend on the particular right triangle chosen, but only on the given angle, since all triangles constructed this way are similar. If, for a given angle α, the opposite side, adjacent side and hypotenuse are labeled O, A and H respectively, then the trigonometric functions are
What is the altitude of a right triangle?
The altitude of a right triangle from its right angle to its hypotenuse is the geometric mean of the lengths of the segments the hypotenuse is split into. Using Pythagoras' theorem on the 3 triangles of sides (p + q, r, s ), (r, p, h ) and (s, h, q ),
What is a Triangle?
A triangle is a regular polygon, with three sides and the sum of any two sides is always greater than the third side. This is a unique property of a triangle. In other words, it can be said that any closed figure with three sides and the sum of all the three internal angles equal to 180°.
What are the different types of triangles?
Types of Tri angles. Acute angle triangle: When the angle between any 2 sides is less than 90 degrees it is called an acute angle triangle. Right angle triangle: When the angle between a pair of sides is equal to 90 degrees it is called a right-angle triangle. Obtuse angle triangle: When the angle between a pair of sides is greater ...
What is the name of the triangle where the sides of the adjacent sides are equal to 90 degrees?
If one of the angles is 90° and the other two angles are equal to 45° each, then the triangle is called an Isosceles Right Angled Triangle, where the adjacent sides to 90° are equal in length. Above were the general properties of the Right angle triangle. The construction of the right angle triangle is also very easy.
What is the difference between a scalene triangle and an isosceles triangle?
Scalene triangle (All the three sides are unequal) Isosceles triangle (Two sides are equal) Equilateral triangle (All the three sides are equal) Note: A scalene triangle and an isosceles triangle both can be a right triangle. A scalene right triangle will have all three sides unequal in length and any of the one angles will be a right angle.
What is the perimeter of a triangle?
Thus the perimeter of the right triangle is the sum of all its three sides. Perimeter of right triangle = Length of (Base + Perpendicular + Hypotenuse) Example: If Base =4cm, Perpendicular= 3cm and Hypotenuse = 5cm.
What is the side opposite of a right angle triangle?
Let us discuss, the properties carried by a right-angle triangle. One angle is always 90° or right angle. The side opposite angle 90° is the hypotenuse. The hypotenuse is always the longest side. The sum of the other two interior angles is equal to 90°.
What is the hypotenuse of the right triangle?
Therefore, the hypotenuse of the right triangle is 10 cm.
What is a right triangle (or right-angled triangle)?
The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90°. The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.
How to find the area of a right triangle?
All that you need are the lengths of the base and the height. In a right triangle, the base and the height are the two sides which form the right angle.
How to find the base of a triangle if you don't know the height?
If you don't know the base or the height, you can find it using the Pythagorean theorem. Use the right triangle calculator to check your calculations or calculate the area of triangles with sides that have larger or decimal value length.
How to solve for hypotenuse in a right triangle?
To solve for c, take the square root of both sides to get c = √ (b²+a²).
What happens if you separate rectangles by diagonals?
If we separate the rectangle by the diagonal, what will we obtain is two right-angled triangles. Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. This means that the area of the rectangle is double that of each triangle.
Which triangle has 2 sides of equal length?
Another of special triangles is the isosceles triangle, which has 2 sides of equal length, and hence two angles of the same size. As opposed to the equilateral triangle, isosceles triangles come in many different shapes, but all have certain properties that are exploited by the isosceles triangle calculator to obtain all the parameters of these triangles.
What are the sets of numbers that satisfy the Pythagorean theorem?
These sets of numbers are called the Pythagorean triplets and are sets of 3 integers (let's call the a, b and c) and satisfy the Pythagorean theorem: a² + b² = c². That is, they could form a right triangle with sides of length a, b and c. The amount of numbers that satisfy this relationship is limited but mathematicians find joy in searching for new ones.
How many types of right angled triangles are there?
There are two types of right angled triangle:
What is a 3 4,5 triangle?
Example: The 3,4,5 Triangle. The " 3,4,5 Triangle " has a right angle in it. (Draw one if you ever need a right angle!) It has no equal sides so it is a scalene right-angled triangle. And, like all triangles, the three angles always add up to 180°.
What is the symmetry of a right triangle?
If a right triangle is isosceles (i.e., its two non-hypotenuse sides are the same length) it has one line of symmetry. Otherwise, the triangle will have no lines of symmetry.
How are right angled triangles similar?
They are similar if all their angles are the same length, or if the ratio of 2 of their sides is the same.
How do you solve a right angle triangle with only one side?
To solve a triangle with one side, you also need one of the non-right angled angles. If not, it is impossible:
How to find side adjacent to angle?
Alternatively, multiply the hypotenuse by cos (θ) to get the side adjacent to the angle .
How to find area of a triangle?
As we remember from basic triangle area formula, we can calculate the area by multiplying triangle height and base and dividing the result by two . A right triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base, so the equation gets simplified to:
How to find the hypotenuse of an angle?
If you have an angle and the side opposite to it, you can divide the side length by sin (θ) to get the hypotenuse. Alternatively, divide the length by tan (θ) to get the length of the side adjacent to the angle.
How to find the missing side of a right triangle?
If you know two other sides of the right triangle, it's the easiest option; all you need to do is apply the Pythagorean theorem: a² + b² = c².
What is a right triangle?
A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.
What is the purpose of knowing the side of a 30°-60° 90° triangle?
As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily . This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.
What is the name of the triangle that divides the original triangle into two smaller triangles that are similar to the original?
The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle. If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle.
What are some examples of Pythagorean triples?
In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc. Area and perimeter of a right triangle are calculated in the same way as any other triangle.
Overview
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle , formerly called a rectangled triangle (Ancient Greek: ὀρθόςγωνία, lit. 'upright angle'), is a triangle in which one angle is a right angle (that is, a 90-degree angle) or two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigono…
Principal properties
As with any triangle, the area is equal to one half the base multiplied by the corresponding height. In a right triangle, if one leg is taken as the base then the other is height, so the area of a right triangle is one half the product of the two legs. As a formula the area T is
where a and b are the legs of the triangle.
Characterizations
A triangle ABC with sides , semiperimeter s, area T, altitude h opposite the longest side, circumradius R, inradius r, exradii ra, rb, rc (tangent to a, b, c respectively), and medians ma, mb, mc is a right triangle if and only if any one of the statements in the following six categories is true. All of them are of course also properties of a right triangle, since characterizations are equivalences.
Trigonometric ratios
The trigonometric functions for acute angles can be defined as ratios of the sides of a right triangle. For a given angle, a right triangle may be constructed with this angle, and the sides labeled opposite, adjacent and hypotenuse with reference to this angle according to the definitions above. These ratios of the sides do not depend on the particular right triangle chosen, but only on the given angle, since all triangles constructed this way are similar. If, for a given ang…
Special right triangles
The values of the trigonometric functions can be evaluated exactly for certain angles using right triangles with special angles. These include the 30-60-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/6, and the 45-45-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/4.
Let H, G, and A be the harmonic mean, the geometric mean, and the arithmetic mean of two positi…
Thales' theorem
Thales' theorem states that if A is any point of the circle with diameter BC (except B or C themselves) ABC is a right triangle where A is the right angle. The converse states that if a right triangle is inscribed in a circle then the hypotenuse will be a diameter of the circle. A corollary is that the length of the hypotenuse is twice the distance from the right angle vertex to the midpoint o…
Medians
The following formulas hold for the medians of a right triangle:
The median on the hypotenuse of a right triangle divides the triangle into two isosceles triangles, because the median equals one-half the hypotenuse.
The medians ma and mb from the legs satisfy
Euler line
In a right triangle, the Euler line contains the median on the hypotenuse—that is, it goes through both the right-angled vertex and the midpoint of the side opposite that vertex. This is because the right triangle's orthocenter, the intersection of its altitudes, falls on the right-angled vertex while its circumcenter, the intersection of its perpendicular bisectors of sides, falls on the midpoint of the hypotenuse.