
Bond convexity
In finance, bond convexity is a measure of the non-linear relationship between price and yield duration of a bond to changes in interest rates, the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the higher the duration, the more sensitive the bond price is to the change in interest rates.
Full Answer
What does convexity mean for bonds?
Convexity is the measure of the curvature in the relationship between a bond’s yield and its price. It illustrates how, as interest rates change, the duration of a bond fluctuates.
Do longer-duration bonds have more convexity?
If a bond's duration increases as yields increase, the bond is said to have negative convexity . If a bond's duration rises and yields fall, the bond is said to have positive convexity.
Why does a callable bond exhibit negative convexity?
Negative convexity occurs when the shape of a bond's yield curve is concave. Most mortgage bonds are negatively convex, and callable bonds usually exhibit negative convexity at lower yields.
Are bond funds riskier than bonds?
While some bonds may be a safer investment than bonds, there are a lot of variables that could affect the relative risks of the two securities. When investing in any type of security, it's important to consider the unique risks of the investment, the price of the investment, and the broader market conditions.
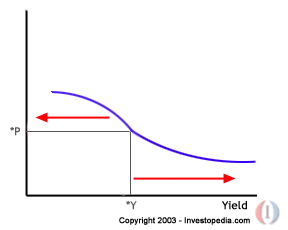
What does bond convexity tell us?
A bond's convexity measures the sensitivity of a bond's duration to changes in yield. Duration is an imperfect way of measuring a bond's price change, as it indicates that this change is linear in nature when in fact it exhibits a sloped or “convex” shape.
Is high convexity good or bad?
Convexity in bonds is a way to measure the bond price's sensitivity to changes in interest rates. Bonds with higher convexity are generally considered better investments in markets where interest rates are expected to rise, and lower convexity is better suited for when rates are likely to remain unchanged or fall.
What does higher convexity mean?
Pointedly: a high convexity bond is more sensitive to changes in interest rates and should consequently witness larger fluctuations in price when interest rates move. The opposite is true of low convexity bonds, whose prices don't fluctuate as much when interest rates change.
Do all bonds have convexity?
Most conventional, non-callable bonds have positive convexity. A bond is callable when the issuer can terminate the bond early by paying the bondholders the original issue price of the bond. Callable bonds, on the other hand, usually have negative convexity. The terms of the call also matter and vary from bond to bond.
Do you want high or low bond convexity?
Positive convexity leads to greater increases in bond prices. If a bond has positive convexity, it would typically experience larger price increases as yields fall, compared to price decreases when yields increase.
Is negative convexity good?
Negative convexity exists when the price of a bond falls as well as interest rates, resulting in a concave yield curve. Assessing a bond's convexity is a great way to measure and manage a portfolio's exposure to market risk.
Do longer bonds have higher convexity?
If you are not feeling experimental, here is a summary of the factors affecting bond convexity: Maturity: Positive correlation; the longer the maturity the greater the convexity/price sensitivity to yield changes.
How do you increase convexity?
To increase convexity, the more distributed future cash flows of a barbell will have higher convexity, but lower yield. To decrease convexity, the more concentrated future cash flows of a bullet will have lower convexity, but higher yield.
How do you find the convexity of a bond?
As can be seen from the formula, Convexity is a function of the bond price, YTM (Yield to maturity), Time to maturity, and the sum of the cash flows. The number of coupon flows (cash flows) change the duration and hence the convexity of the bond.
Is negative convexity bad?
In summary: high, absolute, positive convexity is most likely desirable while high, absolute, negative convexity is most likely less desirable given stable or falling interest rates.
Why is convexity so important?
Convexity is important as it illustrates the impact that changes in yields have on the duration of the bond. As yields approach zero the duration impact of a movement in yields is accentuated.
How do you increase convexity?
To increase convexity, the more distributed future cash flows of a barbell will have higher convexity, but lower yield. To decrease convexity, the more concentrated future cash flows of a bullet will have lower convexity, but higher yield.
Why does barbell have higher convexity?
Convexity is a second-order effect describing a bond's price behavior for larger rate movements and is affected by cash flow dispersion. A barbell portfolio combining short- and long-term bond positions will have greater convexity than a bullet portfolio concentrated in a single maturity for a given duration.
Convexity in Bonds Explained in 5 Minutes
Mike Price is a personal finance writer with more than six years of prior experience working in the banking industry. He specializes in writing about investing, real estate and accounting for The Balance. His work has also been featured in other notable financial websites such as The Motley Fool.
Definition and Example of Convexity in Bonds
Convexity in bonds measures how sensitive the bond’s duration is to changes in interest rates. The higher the convexity, the more the bond price will increase when rates fall—and the less the bond price will drop when rates rise. 1
How Convexity in Bonds Works
Unfortunately for bond investors, calculated numbers like duration and convexity aren’t easy to come by. Professional fund managers use services like Bloomberg to look up this information and you could technically calculate it on your own in Excel, but the best bet is to find a broker’s bond calculator to use.
What It Means for Individual Investors
The first step is to determine what your time frame is. If you’re planning to hold bonds to maturity no matter what, and you have the existing liquidity to pull that off, duration and convexity are irrelevant. Interim prices don’t matter if the plan is to hold through maturity.
What is Bond Convexity?
Bond convexity is the measure of the curvature that arises due to changes in the interest rate and market price of a bond.
What happens if a bond has a positive convexity?
Similarly, if the duration of a bond decreases with a fall in the yield, it is said to have positive convexity. A bond with a positive convexity would see a greater price increase with a fall in its yield. Contrarily, a bond with a negative convexity would see a lower price change due to an increase in the yield.
What is the difference between convexity and duration?
However, duration only considers a linear relationship between bond prices and interest rates . Whereas convexity allows to absorbs effects of other risk factors as well.
What does it mean when bond prices move inversely?
Bond prices and yield move inversely. It means if the yield falls, bond prices rise and vice versa. Investors want to calculate the time it takes to recover their investment. It is called the duration of the bond. It shouldn’t be confused with bond maturity, though, which is simply the lifespan of a bond.
Why is a bond less affected by a change in interest rate?
Generally, a bond with a higher yield will be less affected due to a change in interest rate. It means as the convexity decreases, the investors’ risk decreases due to a change in the interest rates.
What happens if a bond has a high coupon rate?
If a bond offers a high coupon rate, it will be less prone to interest rate changes. For example, a bond with an 8% coupon rate with a market interest rate of 5% is less likely to get affected with an interest rate change than a bond with 6%. The market interest rate would need to go above 8% to make that bond less attractive to existing bondholders.
What does it mean when a bond has a longer duration?
Generally, a longer duration would mean greater interest rate risk for the investors. A bond with a longer duration will take longer to recover the cash flows and will be prone to more interest rate changes.
What is convexity in bond?
Convexity is a good measure for bond price changes with greater fluctuations in the interest rates. Mathematically speaking, convexity is the second derivative ...
What is negative convexity bond?
This type is for a bond that does not have a call option or a prepayment option. Bonds have negative convexity when the yield increases, the duration decreases , i.e., there is a negative correlation between yield and duration, and the yield curve moves downward.
What is the convexity of a bond portfolio?
For a bond portfolio, the convexity would measure the risk of all the bonds put together and is the weighted average of the individual bonds with no bonds or the market value of the bonds being used as weights.
What is positive convexity?
A bond has positive convexity if the yield and the duration of the bond increase or decrease together, i.e., they have a positive correlation#N#Positive Correlation Positive Correlation occurs when two variables display mirror movements, fluctuating in the same direction, and are positively related. In layman's terms, if one variable increases by 10%, the other variable grows by 10% as well, and vice versa. read more#N#. The yield curve for this typically moves upward. This type is for a bond that does not have a call option or a prepayment option. Bonds have negative convexity when the yield increases, the duration decreases, i.e., there is a negative correlation between yield and duration, and the yield curve moves downward. These are typically bonds with call options, mortgage-backed securities, and those bonds which have a repayment option. If the bond with prepayment or call option has a premium to be paid for the early exit, then the convexity may turn positive.
How does periodicity affect the convexity of a bond?
The coupon payments and the periodicity of the payments of the bond contribute to the convexity of the bond. If there are more periodic coupon payments over the life of the bond, then the convexity is higher, making it more immune to interest rate risks as the periodic payments help in negating the effect of the change in the market interest rates. If there is a lump sum payment, then the convexity is the least, making it a more risky investment.
Why is convexity of bonds with a put option positive?
Convexity of bonds with a put option is positive, while that of a bond with a call option is negative. This is because when a put option is in the money.
What is the duration of a bond?
The duration of a bond is the linear relationship between the bond price and interest rates, where, as interest rates increase, bond price decreases. Simply put, a higher duration implies that the bond price is more sensitive to rate changes. For a small and sudden change in bond, yield duration is a good measure of the sensitivity ...
What is convexity in derivatives?
Convexity is a risk management figure, used similarly to the way 'gamma' is used in derivatives risks management; it is a number used to manage the market risk a bond portfolio is exposed to. If the combined convexity and duration of a trading book is high, so is the risk.
How does convexity work?
Convexity is a measure of the curvature or 2nd derivative of how the price of a bond varies with interest rate , i.e. how the duration of a bond changes as the interest rate changes. Specifically, one assumes that the interest rate is constant across the life of the bond and that changes in interest rates occur evenly. Using these assumptions, duration can be formulated as the first derivative of the price function of the bond with respect to the interest rate in question. Then the convexity would be the second derivative of the price function with respect to the interest rate.
What is duration in bond?
Duration is a linear measure or 1st derivative of how the price of a bond changes in response to interest rate changes. As interest rates change, the price is not likely to change linearly, but instead it would change over some curved function of interest rates. The more curved the price function of the bond is, ...
What is effective convexity?
To address this, an effective convexity must be calculated numerically. Effective convexity is a discrete approximation of the second derivative of the bond's value as a function of the interest rate:
How does the present value of a bond decrease as the interest rate increases?
As the interest rate increases, the present value of longer-dated payments declines in relation to earlier coupons (by the discount factor between the early and late payments). However, bond price also declines when interest rate increases, but changes in the present value of sum of each coupons times timing (the numerator in the summation) are larger than changes in the bond price (the denominator in the summation). Therefore, increases in r must decrease the duration (or, in the case of zero-coupon bonds, leave the unmodified duration constant). Note that the modified duration D differs from the regular duration by the factor one over 1+r (shown above), which also decreases as r is increased.
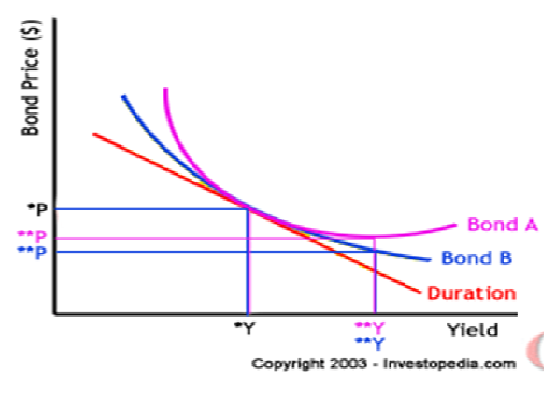
What happens to bond A if yield increases?
This means if yield increases further, the price of bond A may fall drastically while the price of bond B won’t change; i.e. bond B holders are expecting a price rise any moment and are therefore reluctant to sell it off, while bond A holders are expecting further price-fall and are ready to dispose of it.
What does "less convexity" mean?
Less convexity means less price-volatility or risk; less risk means less return.
What is the convexity of a bond?
Convexity, a measure of the curvature of the changes in the price of a bond, in relation to changes in interest rates, addresses this error, by measuring the change in duration, as interest rates fluctuate. The formula is as follows:
What Are Duration and Convexity?
Duration and convexity are two tools used to manage the risk exposure of fixed-income investments. Duration measures the bond's sensitivity to interest rate changes. Convexity relates to the interaction between a bond's price and its yield as it experiences changes in interest rates.
Why do investors need to measure the duration of a bond?
With coupon bonds, investors rely on a metric known as duration to measure a bond's price sensitivity to changes in interest rates. Because a coupon bond makes a series of payments over its lifetime, fixed-income investors need ways to measure the average maturity of a bond's promised cash flow, to serve as a summary statistic of the bond’s effective maturity. The duration accomplishes this, letting fixed-income investors more effectively gauge uncertainty when managing their portfolios.
What is the duration of a zero-coupon bond?
The duration of a zero-coupon bond equals time to maturity. Holding maturity constant, a bond's duration is lower when the coupon rate is higher, because of the impact of early higher coupon payments. Holding the coupon rate constant, a bond's duration generally increases with time to maturity. But there are exceptions, as with instruments such as ...
What is the effect of interest rate change on fixed income?
Ever-changing interest rates introduce uncertainty in fixed-income investing. Duration and convexity let investors quantify this uncertainty, helping them manage their fixed-income portfolios.
Which bond has the highest convexity?
Zero-coupon bonds have the highest convexity, where relationships are only valid when the compared bonds have the same duration and yields to maturity. Pointedly: a high convexity bond is more sensitive to changes in interest rates and should consequently witness larger fluctuations in price when interest rates move.
What is the term used to measure the price sensitivity of a bond?
With coupon bonds, investors rely on a metric known as “duration” to measure a bond's price sensitivity to changes in interest rates.
What is convexity in bond?
In the bond world, convexity is simply defined as a measure of the sensitivity of the bonds duration to change its yield. Convexity is believed to be a good measure for bond price changes that are accompanied by greater fluctuations in their interest rates. Mathematically, convexity is the second derivative of the formula for change in bond prices with a change in interest rates and a first derivative of the duration equation. The duration of the changes in a bond in relation to the changes in its interest rate can be demonstrated by using convexity. This has enabled the measurement and management of the portfolio's exposure to interest rate risk by portfolio managers who use convexity as a risk-management tool.
What is a negative convexity bond?
A bond is said to have a negative convexity if there is an increase in its duration as its yields increase. That is, there will be a decline in the bond price by a greater rate when there is a rise in yields than if yields had fallen. Therefore, a bond whose price falls with an increased duration is said to have negative convexity. A positive convexity bond, on the other hand, is one whose bond duration rises as yields fall. That is, there will be a rise in the bond price by a greater rate when there is a fall in yields than if yields had risen.
What happens to the yields of bonds when interest rates increase?
When it comes to yields and interest rates, as the interest rate increases, the price of bonds returning less than the increment rate attained by the interest rate will fall. A rise in market rates will lead to a rise in the yields of new bonds coming on the market as they are being issued at the new, higher rates. Also, investors demand a higher yield from the bonds they buy, as rates increases. If they expect a future rise in interest rates, they don't want a fixed-rate bond at current yields. Hence, the issuer of these debt vehicles must also raise their yields to remain competitive when interest rates increase.
Why is convexity better than duration?
Though duration is a good tool for measuring the effect of small and sudden fluctuations in interest rates on bond prices, convexity is a better tool because it measures the impact of large interest rate fluctuations on bond prices. The rate of exposure of the portfolio to systemic risk increases as convexity increases, and vice versa. Generally, the higher the yield, the lower the convexity of a bond.
What is bond duration?
Bond duration is an approximate measure of a bond's price sensitivity to changes in interest rates. An increase in a bond's duration implies that there will be a movement to a greater degree by the bond's price in the opposite direction of the rates. Alternately, a decrease in this figure will lead to a decreased movement in the debt instrument. If for instance, a bond has a duration of 6 years, its price will rise by about 6%, if its yield drops by a percentage point (100 basis points), and its price will fall by about 6%, if its yield rises by that amount.
How to understand convexity?
To understand convexity, it's necessary to understand the relationship between bond prices and market interest rates. The lower the interest rate, the higher the bond price, and vice versa. As interest rates increases, the bond may suffer a decrement in the earnings they may offer a potential investor when compared to other securities. This can be said to be the cause of the oppositereaction between bond prices and interest rates. The earnings or returns expected to be made by an investor through the acquisition or a holding of a particular security is known as the bond yield. Several characteristics including the market interest rates which can change regularly are largely dependent on by bond prices.
How are bond prices and interest rates related?
Bond prices and interest rates are inversely related. A rise in interest rates will lead to a fall in bond prices, and some degree of pain will be felt by bond investors, especially those who remain in bond funds. In a market experiencing rising rates, bondholders will look to sell their existing bonds and acquire newly-issued bonds that are paying higher yields. The presence of lower rates selling bonds on the market will cause a drop in the prices of these debt holdings. An investor may have to wait for a stop in the rising rates before buying the higher-yielding security. This results in an inverse relationship between the two.
Why Are Bonds Convex?
When yields increase to 11%, we see how the holder of the bond experiences a shortfall, relative to a par bond, of $5 each period. The impact on the bond’s price is simply the present value of the stream of $5 shortfall amounts, which totals to a drop of $59.75. Relative to par, this bond should be worth $59.75 less, resulting in a bond price of $940.25.
What happens to a bond when its yield decreases?
As a bond yield decreases, its price rises at an increasing rate, whereas a bond’s price falls at a decreasing rate as its yield increases. This phenomenon is known as convexity.
What is the second derivative of convexity?
In the parlance of those who know calculus, convexity is the second derivative. For the layperson this is known as the rate of change in change. For convexity to make better sense, let me compare it to driving a car. When you are driving a car your speed is the rate of change in the car’s location.
What is the negative correlation of yield?
Yield: Negative correlation; the lower the yield the higher the convexity/price sensitivity to yield changes. To best understand this, look at the graph above for the 30-year bond. The lower the yield goes the higher the convexity/price sensitivity as compared with the higher yield portion of the curve.
Is a bond price sensitive to maturity?
What all of this means is that a bond’s price is sensitive to the length of its maturity. But it is also sensitive to other factors. I have created a spreadsheet that aptly demonstrates convexity for a bond under different scenarios so that you can experiment with different combinations of factors to show you the effects ...
Is maturity a positive correlation?
Maturity: Positive correlation; the longer the maturity the greater the convexity/price sensitivity to yield changes.
What is the convexity of a bond?
Convexity: As the yield on a bond changes so too does its duration, a bond’s convexity measures the sensitivity of a bond’s duration to changes in yield. Duration is an imperfect way of measuring a bond’s price change, as it indicates that this change is linear in nature when in fact it exhibits a sloped or “convex” shape.
Why do bonds have positive convexity?
A bond with positive convexity will have larger price increases due to a decline in yields than price declines due to an increase in yields. Positive convexity can be thought of as working in the investor’s favor, since the price becomes less sensitive when yields rise (prices down) than when yields decline (prices up).
What are the two metrics used to help investors understand how the price of a bond will be affected by changes in interest?
Duration and convexity are two metrics used to help investors understand how the price of a bond will be affected by changes in interest rates. How a bond’s price responds to changes in interest rates is measured by its duration, and can help investors understand the implications for a bond’s price should interest rates change.
How does a bond's price change?
As a general rule, the price of a bond moves inversely to changes in interest rates: a bond’s price will increase as rates decline and will decrease as rates move up. Macaulay duration is the weighted-average maturity of a bond’s cashflows, which is measured in years. Modified duration attempts to estimate how the price of a bond will change in response to a change in interest rates and is stated in terms of a percentage change in price. Typically when duration is quoted it is referring to a bond’s modified duration rather than Macaulay duration. Taking this concept one step further, a bond’s convexity is a measurement of how duration changes as yields change. These two measurements can provide insight into how a bond is expected to perform should interest rates change and can help investors understand the price risk of fixed income securities in different interest rate environments.
How to determine duration of bond?
The duration of a bond is primarily affected by its coupon rate, yield, and remaining time to maturity. The duration of a bond will be higher the lower its coupon. Duration will be higher the lower its yield. Duration will also be higher the longer its maturity. The following scenarios of comparing two bonds should help clarify how these three traits affect a bond’s duration: 1 If the coupon and yield are the same, duration increases with time left to maturity 2 If the maturity and yield are the same, duration increases with a lower coupon 3 If the coupon and maturity are the same, duration increases with a lower yield
What happens to bonds when rates decline?
If rates are expected to decline, consider bonds with higher durations. As yields decline and bond prices move up, higher duration bonds stand to gain more than their lower duration counterparts.
What happens to the duration of a coupon if the yield and coupon are the same?
If the coupon and yield are the same, duration increases with time left to maturity. If the maturity and yield are the same, duration increases with a lower coupon. If the coupon and maturity are the same, duration increases with a lower yield.
Definition and Example of Convexity in Bonds
- Convexity in bonds measures how sensitive the bond’s duration is to changes in interest rates. The higher the convexity, the less the bond price will increase when rates fall—and the less the bond price will drop when rates rise.1 First, let’s go over the relationship between bond prices and interest rates and explain how bond durationworks. Bond p...
How Convexity in Bonds Works
- Unfortunately for bond investors, calculated numbers like duration and convexity aren’t easy to come by. Professional fund managers use services like Bloomberg to look up this information and you could technically calculate it on your own in Excel, but the best bet is to find a broker’s bond calculator to use. Taking the time to learn the formula and modify and apply it in Excel probably i…
What It Means For Individual Investors
- The first step is to determine what your time frameis. If you’re planning to hold bonds to maturity no matter what, and you have the existing liquidity to pull that off, duration and convexity are irrelevant. Interim prices don’t matter if the plan is to hold through maturity. Duration is more relevant for short-term holdings. It can help you figure out what will happen as a result of small c…
Explanation
Calculation of Convexity Example
Convexity Approximation Formula
Convexity and Risk Management
Positive and Negative Convexity
Convexity of A Bond Portfolio
- For a bond portfolio, the convexity would measure the risk of all the bonds put together and is the weighted average of the individual bonds with no bonds or the market value of the bonds being used as weights. Even though Convexity takes into account the non-linear shape of the price-yield curve and adjusts for the prediction for price change, the...
Interest Rate Risk and Convexity
Conclusion
Recommended Articles
Overview
In finance, bond convexity is a measure of the non-linear relationship of bond prices to changes in interest rates, the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the higher the duration, the more sensitive the bond price is to the change in interest rates. Bond convexity is one of the most basic and widely used forms of convexity in finance. Convexity was based on the work of Hon-Fei Lai and popularized by Stanle…
Calculation of convexity
Why bond convexities may differ
Mathematical definition
Application of convexity
Effective convexity
See also
Further reading