Summary
- Heteroskedasticity refers to a situation where the variance of the residuals is unequal over a range of measured values.
- If heteroskedasticity exists, the population used in the regression contains unequal variance, the analysis results may be invalid.
- Models involving a wide range of values are supposedly more prone to heteroskedasticity.
What is the effect of heteroscedasticity in OLS?
Heteroscedasticity tends to produce p-values that are smaller than they should be. This effect occurs because heteroscedasticity increases the variance of the coefficient estimates but the OLS procedure does not detect this increase. Consequently, OLS calculates the t-values and F-values using an underestimated amount of variance.
What is heteroscedasticity in regression?
Specifically, heteroscedasticity is a systematic change in the spread of the residuals over the range of measured values. Heteroscedasticity is a problem because ordinary least squares (OLS) regression assumes that all residuals are drawn from a population that has a constant variance (homoscedasticity).
What are the tell-tale signs of heteroskedasticity?
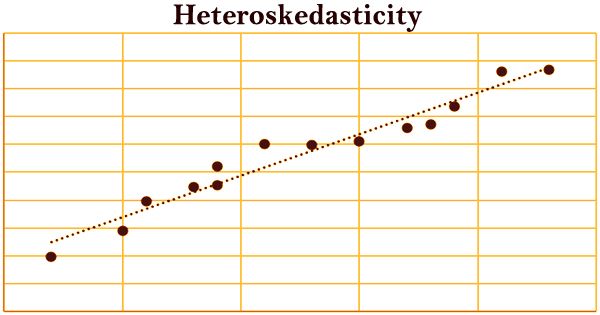
With heteroskedasticity, the tell-tale sign upon visual inspection of the residual errors is that they will tend to fan out over time, as depicted in the image below. Heteroskedasticity often arises in two forms: conditional and unconditional.
What is the opposite of heteroskedastic?
The opposite of heteroskedastic is homoskedastic. Homoskedasticity refers to a condition in which the variance of the residual term is constant or nearly so. Homoskedasticity is one assumption of linear regression modeling.

What are the consequences of heteroskedasticity?
Consequences of Heteroscedasticity The OLS estimators and regression predictions based on them remains unbiased and consistent. The OLS estimators are no longer the BLUE (Best Linear Unbiased Estimators) because they are no longer efficient, so the regression predictions will be inefficient too.
Does heteroskedasticity affect prediction?
The prediction will not be altered in any way by using het-robust standard errors. It remains the same and is still valid.
Why is heteroskedasticity a problem?
Heteroscedasticity is a problem because ordinary least squares (OLS) regression assumes that all residuals are drawn from a population that has a constant variance (homoscedasticity). To satisfy the regression assumptions and be able to trust the results, the residuals should have a constant variance.
Why is heteroscedasticity important?
The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance.
Does heteroskedasticity cause inconsistency?
plays no role in showing whether OLS was unbiased or consistent. If heteroskedasticity does not cause bias or inconsistency in the OLS estimators, why did we introduce it as one of the Gauss-Markov assumptions? The estimators of the variances, V (ˆβj), are biased without the homoskedasticity assumption.
What we can say about the heteroskedasticity in linear regression?
Heteroskedasticity refers to situations where the variance of the residuals is unequal over a range of measured values. When running a regression analysis, heteroskedasticity results in an unequal scatter of the residuals (also known as the error term).
What is the relationship between heteroskedasticity and bias?
While heteroskedasticity does not cause bias in the coefficient estimates, it does make them less precise; lower precision increases the likelihood that the coefficient estimates are further from the correct population value.
What is heteroscedasticity What are the causes and consequences of heteroscedasticity?
Heteroscedasticity is mainly due to the presence of outlier in the data. Outlier in Heteroscedasticity means that the observations that are either small or large with respect to the other observations are present in the sample. Heteroscedasticity is also caused due to omission of variables from the model.
What happens if heteroskedasticity exists?
If heteroskedasticity exists, the population used in the regression contains unequal variance, the analysis results may be invalid.
How to find heteroskedasticity?
One of the most common ways of checking for heteroskedasticity is by plotting a graph of the residuals.
What is heteroskedasticity in regression?
What is Heteroskedasticity? Heteroskedasticity refers to situations where the variance of the residuals is unequal over a range of measured values. When running a regression analysis, heteroskedasticity results in an unequal scatter of the residuals (also known as the error term).
Why is heteroskedasticity more likely in regression models?
It has been shown that models involving a wide range of values are more prone to heteroskedasticity because the differences between the smallest and largest values are so significant.
When residuals have unequal variance, it is known as: "Homoskedasticity"?
However, when the residuals have constant variance, it is known as homoskedasticity . Homoskedasticity refers to situations where the residuals are equal across all the independent variables.
What are the two types of heteroskedasticity?
When heteroskedasticity exists in a regression, it can be categorized into two types: pure and impure heteroskedasticity: Pure heteroskedasticity refers to situations where the correct number of independent variables.
What happens if there is an unequal scatter of residuals?
If there is an unequal scatter of residuals, the population used in the regression contains unequal variance, and therefore the analysis results may be invalid.
Why is heteroscedasticity a problem?
Heteroscedasticity is a problem because ordinary least squares (OLS) regression assumes that the residuals come from a population that has homoscedasticity, which means constant variance. When heteroscedasticity is present in a regression analysis, the results of the analysis become hard to trust.
How to find heteroscedasticity?
The simplest way to detect heteroscedasticity is with a fitted value vs. residual plot.
What is heteroscedastic regression?
In regression analysis, heteroscedasticity (sometimes spelled heteroskedasticity) refers to the unequal scatter of residuals or error terms. Specfically, it refers to the case where there is a systematic change in the spread of the residuals over the range of measured values.
Can you spot heteroscedasticity using a fitted value vs residual plot?
However, by using a fitted value vs. residual plot, it can be fairly easy to spot heteroscedasticity.
What is heteroscedasticity in regression?
Heteroscedasticity can also arise as a result of the presence of outliers. The inclusion or exclusion of such observations, especially when the sample size is small, can substantially alter the results of regression analysis.
What is the source of heteroscedasticity?
Incorrect data transformation, incorrect functional form (linear or log-linear model) is also the source of heteroscedasticity
Why are OLS estimators no longer blue?
The OLS estimators are no longer the BLUE (Best Linear Unbiased Estimators) because they are no longer efficient, so the regression predictions will be inefficient too.
Is heteroscedasticity more common in time series than in cross sectional data?
Note: Problems of heteroscedasticity is likely to be more common in cross-sectional than in time series data .
What Problems Does Heteroscedasticity Cause?
Anytime that you violate an assumption, there is a chance that you can’t trust the statistical results.
How to check heteroscedasticity?
To check for heteroscedasticity, you need to assess the residuals by fitted value plots specifically. Typically, the telltale pattern for heteroscedasticity is that as the fitted values increases, the variance of the residuals also increases.
What is heteroscedasticity in regression?
Specifically, heteroscedasticity is a systematic change in the spread of the residuals over the range of measured values. Heteroscedasticity is a problem because ordinary least squares ( OLS) ...
Why do cross sectional studies have a larger risk of residuals with non-constant variance?
Cross-sectional studies have a larger risk of residuals with non-constant variance because of the larger disparity between the largest and smallest values. For our study, imagine the huge range of populations from towns to the major cities!
Why is weighted regression more data manipulation?
For one thing, weighted regression involves more data manipulation because it applies the weights to all variables. It’s also less intuitive. And, if you skip straight to this, you might miss the opportunity to specify a more meaningful model by redefining the variables.
How does heteroscedasticity affect household consumption?
If you model household consumption based on income, you’ll find that the variability in consumption increases as income increases. Lower income households are less variable in absolute terms because they need to focus on necessities and there is less room for different spending habits. Higher income households can purchase a wide variety of luxury items, or not, which results in a broader spread of spending habits.
What are some examples of cross-sectional studies?
For example, a cross-sectional study that involves the United States can have very low values for Delaware and very high values for California. Similarly, cross-sectional studies of incomes can have a range that extends from poverty to billionaires.
How to detect heteroscedasticity?
I am going to illustrate this with an actual regression model based on the cars dataset, that comes built-in with R. Lets first build the model using the lm () function.
Why do we check for heteroscedasticity of residuals?
The reason is, we want to check if the model thus built is unable to explain some pattern in the response variable Y Y, that eventually shows up in the residuals. This would result in an inefficient and unstable regression model that could yield bizarre predictions later on.
Is heteroscedsticity solved?
Ah, we have a much flatter line and an evenly distributed residuals in the top-left plot. So the problem of heteroscedsticity is solved and the case is closed. If you have any question post a comment below.
Further Analyzing Heteroskedasticity
- To look for heteroskedasticity, it’s necessary to first run a regression and analyze the residuals. One of the most common ways of checking for heteroskedasticity is by plotting a graph of the residuals. Visually, if there appears to be a fan or cone shape in the residual plot, it indicates the presence of heteroskedasticity. Also, regressions with heteroskedasticity show a pattern where …
Causes of Heteroskedasticity
- There are many reasons why heteroskedasticity may occur in regression models, but it typically involves problems with the dataset. It has been shown that models involving a wide range of values are more prone to heteroskedasticity because the differences between the smallest and largest values are so significant. For example, suppose a dataset contains values that range fro…
Heteroskedasticity vs. Homoskedasticity
- When analyzing regression results, it’s important to ensure that the residuals have a constant variance. When the residuals are observed to have unequal variance, it indicates the presence of heteroskedasticity. However, when the residuals have constant variance, it is known as homoskedasticity. Homoskedasticity refers to situations where the resid...
Real-World Example
- One common example of heteroskedasticity is the relationship between food expenditures and income. For those with lower incomes, their food expenditures are often restricted based on their budget. As incomes increase, people tend to spend more on food as they have more options and fewer budget restrictions. For wealthier people, they can access a variety of foods with very few …
Additional Resources
- Thank you for reading CFI’s guide to Heteroskedasticity. In order to help you become a world-class analyst and advance your career to your fullest potential, these additional resources will be very helpful: 1. Free Statistics Fundamentals Course 2. Homoskedastic 3. Variance Formula 4. Regression Analysis 5. Random Variable