A 2×3 factorial design is a type of experimental design that allows researchers to understand the effects of two independent variables on a single dependent variable. In this type of design, one independent variable has two levels and the other independent variable has three levels.
What is a 2 x 2 factorial design?
In this example, we can say that we have a 2 x 2 (spoken “two-by-two) factorial design. In this notation, the number of numbers tells you how many factors there are and the number values tell you how many levels. If I said I had a 3 x 4 factorial design, you would know that I had 2 factors and that one factor had 3 levels while the other had 4.
What are the three levels of factorial design?
The three-level design is written as a 3 k factorial design. It means that k factors are considered, each at 3 levels. These are (usually) referred to as low, intermediate and high levels. These levels are numerically expressed as 0, 1, and 2.
What is a 2^3 factorial design example?
Example for 2^3 Factorial Design • An experiment was laid out with four replications to test the effect of two levels of N (N0= 0 kg/ ha, N1= 40 kg/ha) and two levels of P (P0= 0 kg/ha, P1= 30 kg/ha) and two levels of K (K0= 0 kg/ha, K1= 20 kg/ha) on the field of paddy.
How many runs are there in a two level full factorial design?
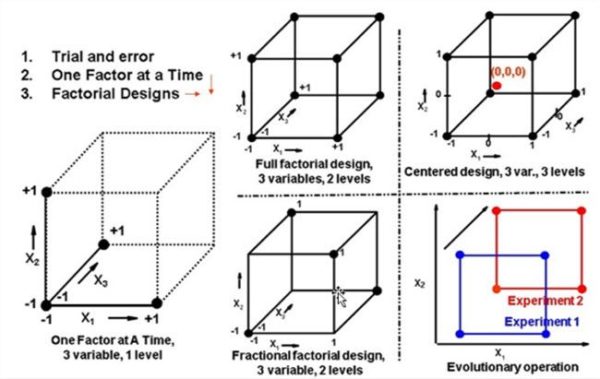
Two-level full factorial designs Description Graphical representation of a two-level design with 3 factors Consider the two-level, full factorial design for three factors, namely the 23design. This implies eight runs (not counting replications or center point runs). Graphically, we can represent the 23design by the cube shown in Figure 3.1.

How many factors are there in a 2x3 factorial design?
three factorsA factorial design is one involving two or more factors in a single experiment. Such designs are classified by the number of levels of each factor and the number of factors. So a 2x2 factorial will have two levels or two factors and a 2x3 factorial will have three factors each at two levels.
How do you solve 2/3 Factorials?
0:122:382^3 Factorial Designs - YouTubeYouTubeStart of suggested clipEnd of suggested clipOrder as you can see factor 1 changes every trial factor to every two trials and factor 3 every 4 soMoreOrder as you can see factor 1 changes every trial factor to every two trials and factor 3 every 4 so on and so on for as many factors as you're checking.
How many independent variables are in a 2x3 factorial design?
In a 2x3 design there are two IVs. IV1 has two levels, and IV2 has three levels.
What is a 3 by 2 design?
This is the simplest three-level design. It has two factors, each at three levels. The 9 treatment combinations for this type of design can be shown pictorially as follows: FIGURE 3.23: A 32 Design Schematic. A notation such as "20" means that factor A is at its high level (2) and factor B is at its low level (0).
How many main effects does a 2x2x2 factorial design have?
If you had a 2x2x2 design, you would measure three main effects, one for each IV.
What is a 2x4 factorial design?
A factorial design is an experiment with two or more factors (independent variables). 2 x 4 design means two independent variables, one with 2 levels and one with 4 levels. "condition" or "groups" is calculated by multiplying the levels, so a 2x4 design has 8 different conditions.
What is a 3x2 factorial ANOVA?
3x2 = There are two IVs, the first IV has three levels, the second IV has two levels. There are a total of 6 conditions, 3x2=6. 4x4 = There are two IVs, the first IV has 4 levels, the second IV has 4 levels. There are a total of 16 condition, 4x4=16. 2x3x2 = There are a total of three IVs.
How many groups are in a 2x3 ANOVA?
3. In a one-way ANOVA, the one factor or independent variable analyzed has three or more categorical groups....One-Way ANOVATwo-Way ANOVANumber of Groups of SamplesThree or more.Each variable should have multiple samples.3 more rows•Jul 20, 2018
How many participants do I need for a 2x2 study?
If your dependent variable is interval/ratio, I would recommend at least 30 in each cell.
What is a 2 by 2 factorial design?
an experimental design in which there are two independent variables each having two levels. When this design is depicted as a matrix, two rows represent one of the independent variables and two columns represent the other independent variable. Also called two-by-two design; two-way factorial design.
What are three types of factorial designs?
There are three main types of factorial designs, namely “Within Subject Factorial Design”, “Between Subject Factorial Design”, and “Mixed Factorial Design”. Within Subject Factorial Design: In this factorial design, all of the independent variables are manipulated within subjects.
What is an example of a factorial design?
So, for example, a 4×3 factorial design would involve two independent variables with four levels for one IV and three levels for the other IV.
How many main effects are there in a 2x3 factorial design quizlet?
If a researcher were interested in studying how two independent variables work together to influence a dependent variable, the best design to use would be a higher order factorial design. In a 2 by 3 design, there are two possible main effects. In a two by four design, there are six possible main effects.
What is 2k factorial design?
The first design in the series is one with only two factors, say A and B, each at two levels. • This design is called a 2. 2 factorial design. • The levels of the factors may be called 'low' and 'high'.
What is 2 level factorial design?
Full two-level factorial designs are carried out to determine whether certain. factors or interactions between two or more factors have an effect on the response. and to estimate the magnitude of that effect.
How do you find the number of interactions in a factorial design?
0:5711:31Factorial Designs: Main Effects & Interactions - YouTubeYouTubeStart of suggested clipEnd of suggested clipNow this particular design can be further called a 2x2 factorial. Design where each of these twosMoreNow this particular design can be further called a 2x2 factorial. Design where each of these twos corresponds to an independent variable and the number of levels actually in that independent variable.
A Closer Look at Factorial Designs
As you may recall, the independent variable is the variable of interest that the experimenter will manipulate. The dependent variable, on the other hand, is the variable that the researcher then measures. By doing this, psychologists can see if making changes to the independent variable results in some type of change in the dependent variable.
The Advantages and Challenges of Using Factorial Designs
One of the big advantages of factorial designs is that they allow researchers to look for interactions between independent variables. An interaction is a result in which the effects of one experimental manipulation depends upon the experimental manipulation of another independent variable.
Examples of Factorial Designs
A university wants to assess the starting salaries of their MBA graduates. The study looks at graduates working in four different employment areas: accounting, management, finance, and marketing. In addition to looking at the employment sector, the researchers also look at gender.
How to tell if there is an interaction in factorial design?
How do you know if there is an interaction in a factorial design? There are three ways you can determine there’s an interaction. First, when you run the statistical analysis, the statistical table will report on all main effects and interactions. Second, you know there’s an interaction when can’t talk about effect on one factor without mentioning the other factor. if you can say at the end of our study that time in instruction makes a difference, then you know that you have a main effect and not an interaction (because you did not have to mention the setting factor when describing the results for time). On the other hand, when you have an interaction it is impossible to describe your results accurately without mentioning both factors. Finally, you can always spot an interaction in the graphs of group means – whenever there are lines that are not parallel there is an interaction present! If you check out the main effect graphs above, you will notice that all of the lines within a graph are parallel. In contrast, for all of the interaction graphs, you will see that the lines are not parallel.
How to understand factorial design?
Probably the easiest way to begin understanding factorial designs is by looking at an example. Let’s imagine a design where we have an educational program where we would like to look at a variety of program variations to see which works best. For instance, we would like to vary the amount of time the children receive instruction with one group getting 1 hour of instruction per week and another getting 4 hours per week. And, we’d like to vary the setting with one group getting the instruction in-class (probably pulled off into a corner of the classroom) and the other group being pulled-out of the classroom for instruction in another room. We could think about having four separate groups to do this, but when we are varying the amount of time in instruction, what setting would we use: in-class or pull-out? And, when we were studying setting, what amount of instruction time would we use: 1 hour, 4 hours, or something else?
What is a factor in factorial design?
Let’s begin by doing some defining of terms. In factorial designs, a factor is a major independent variable. In this example we have two factors: time in instruction and setting. A level is a subdivision of a factor. In this example, time in instruction has two levels and setting has two levels. Sometimes we depict a factorial design with a numbering notation. In this example, we can say that we have a 2 x 2 (spoken “two-by-two) factorial design. In this notation, the number of numbers tells you how many factors there are and the number values tell you how many levels. If I said I had a 3 x 4 factorial design, you would know that I had 2 factors and that one factor had 3 levels while the other had 4. Order of the numbers makes no difference and we could just as easily term this a 4 x 3 factorial design. The number of different treatment groups that we have in any factorial design can easily be determined by multiplying through the number notation. For instance, in our example we have 2 x 2 = 4 groups. In our notational example, we would need 3 x 4 = 12 groups.
What is null case?
Let’s begin by looking at the “null” case. The null case is a situation where the treatments have no effect. This figure assumes that even if we didn’t give the training we could expect that students would score a 5 on average on the outcome test. You can see in this hypothetical case that all four groups score an average of 5 and therefore the row and column averages must be 5. You can’t see the lines for both levels in the graphs because one line falls right on top of the other.
Why is factorial design important?
Factorial design has several important features. First, it has great flexibility for exploring or enhancing the “signal” (treatment) in our studies. Whenever we are interested in examining treatment variations, factorial designs should be strong candidates as the designs of choice.
What is the main effect?
The Main Effects. A main effect is an outcome that is a consistent difference between levels of a factor. For instance, we would say there’s a main effect for setting if we find a statistical difference between the averages for the in-class and pull-out groups, at all levels of time in instruction.
What is interaction effect?
An interaction effect exists when differences on one factor depend on the level you are on another factor. It’s important to recognize that an interaction is between factors, not levels. We wouldn’t say there’s an interaction between 4 hours/week and in-class treatment.
How does Box-Behnken factorial design help?
Box-Behnken factorial design can help in the optimization of nanocarrier formulations. For instance, formulation variables of NPs loaded with the anti-HIV microbicide Tenofovir, formulated following a gelation method, were investigated [28]. The influence of three formulation factors was considered: chitosan concentration, sodium triphosphate pentabasic (STP)/chitosan weight ratio, and Tenofovir/chitosan weight ratio. The optimal formulation based on a mathematical optimization process produced NPs with a size of ≈ 210 nm with a relatively low encapsulation efficiency (EE%, ≈ 5%). To improve the EE values, a 50% ( v /v) ethanol/water mixture was used as a solvent for chitosan. While the use of ethanol resulted in EE of ≈ 20%, size increased to ≈ 600 nm. Increased mucoadhesive ability from 6% to 12% was observed when the particle size decreased from 900 to ≈ 190 nm. Considering factors of EE and mucoadhesive ability, larger-sized NPs were proved the most efficient. Similarly, Tenofovir-loaded solid lipid nanoparticles (SLNs) were prepared by a modified phase inversion technique, and the effect of bovine serum albumin (BSA) concentration, pH of the aqueous phase, and lipid amount (Softisan 100) on the particle mean diameter [29] was evaluated. Box-Behnken factorial design predicted that an increase in both the concentration of BSA and pH has a significant decreasing effect on the particle size. In a more recent work, Box-Behnken factorial design enabled the optimization of PLGA NPs loaded with the anti-HIV microbicide dapivirine [30]. Factors such as the volume of ethyl acetate, the concentration of PVA solution, and the intensity of sonication were explored for their effects on the NP characteristics. Optimized NPs produced by an emulsion solvent evaporation method were monodisperse with a diameter of ≈ 170 nm. Such statistical design can be used as a useful tool in the design of nanocarriers with defined properties.
What are the disadvantages of factorial design?
One of the disadvantages of factorial designs is the very large number of experiments required when working with more than two or three factors. As the number of factors increases, the number of experiments required for a two-level factorial design increases in the geometric progression 2, 4, 8, 16, 32, ….
How to evaluate factorial design?
Another way to evaluate factorial designs is to fit a linear response model to the observed data. As shown above, such a model can be seen as an approximation of the underlying, but unknown, response function, f, by a truncated Taylor expansion. For this, the experimental variable should be continuous and the Taylor polynomial defines a response surface. We can also fit polynomial models with discrete variables at two levels. For this, we use dummy variables, xi, to define the discrete settings. The value xi = − 1 is assigned to one of the discrete settings, and xi = 1 to the other. The model is fitted and from the coefficients of the discrete variables it is possible to evaluate how the discrete changes influence on the response. It is also possible to evaluate interactions between discrete variables and other variables from their cross-product coefficients. However, such models cannot be interpreted geometrically as response surfaces.
What is the simplest factorial design?
The simplest factorial designs are those that involve just two levels of each of the factors. Figure 1 shows the locations of experiments associated with a two-level two-factor factorial design and Fig. 2 shows the locations of experiments associated with a two-level three-factor factorial design.
What are factororial designs?
Factorial designs have been used to determine the effect that numerous parameters have on the process, including temperature, pressure, pretreatment of sample, extraction time, fluid flow rate, and addition of a modifier .
How fast can you grind sapphire?
They show that wheel speeds of 9.8 m/s to 16 m/s have a significant effect on the surface finish of sapphire. Feed rates from 0.5 m/min to 2 m/min also have an effect but this is not as significant as wheel speed.
How to get the model matrix?
The model matrix, X, contains a column corresponding to each term in the model. It is obtained from the design matrix D by appending a column of ones. I, corresponding to the constant term β 0, and a column for the cross-product x1x2. The model matrix is shown in Table 13.
What is a 3 level design?
The three-level design is written as a 3 k factorial design. It means that k factors are considered, each at 3 levels. These are (usually) referred to as low, intermediate and high levels. These levels are numerically expressed as 0, 1, and 2. One could have considered the digits -1, 0, and +1, but this may be confusing with respect to the 2-level designs since 0 is reserved for center points. Therefore, we will use the 0, 1, 2 scheme. The reason that the three-level designs were proposed is to model possible curvature in the response function and to handle the case of nominal factors at 3 levels. A third level for a continuous factor facilitates investigation of a quadratic relationship between the response and each of the factors.
How many degrees of freedom are there in a two factor interaction?
where each factor is included as a nominal factor rather than as a continuous variable. In such cases, main effects have 2 degrees of freedom, two-factor interactions have 2 2 = 4 degrees of freedom and k -factor interactions have 2 k degrees of freedom. The model contains 2 + 2 + 2 + 4 + 4 + 4 + 8 = 26 degrees of freedom. Note that if there is no replication, the fit is exact and there is no error term (the epsilon term) in the model. In this no replication case, if one assumes that there are no three-factor interactions, then one can use these 8 degrees of freedom for error estimation.
What does 20 mean in math?
A notation such as "20" means that factor A is at its high level (2) and factor B is at its low level (0).
Is 3 level design prohibitive?
Unfortunately, the three-level design is prohibitive in terms of the number of runs, and thus in terms of cost and effort. For example a two-level design with center points is much less expensive while it still is a very good (and simple) way to establish the presence or absence of curvature.
Why is factorial design important?
The increased use of factorial designs in research has come about largely because they are. better at testing several causal hypotheses within a single design.
What is independent variable?
independent variable; levels of each independent variable . In most factorial studies, the primary focus is on. the interaction effects of the independent variables on the dependent variables.
How many participants are needed for a factorial design?
In a within-subjects factorial design, we need 10 participants in each of the four cells. Therefore, in total, we need
What is the ANOVA summary table?
The results of an A NOVA are typically presented in. an ANOVA summary table. In the type of mixed design in which both between-subjects and within-subjects factors exist in the same study, the critical issue is. that the statistical procedures must take into account the correlated nature of some of the data.
How many interactions are there in a main effect?
Whenever main effects are found, there must be at least one interaction.
What is statistical removal?
the statistical removal of variability caused by extraneous variables.
What is plotting the means?
Plotting the means is a visualize way to inspect the effects that the independent variables have on the dependent variable. However, we can also perform a two-way ANOVA to formally test whether or not the independent variables have a statistically significant relationship with the dependent variable. -For example, the following code shows how ...
Why do we use 2x2 factorial design?
When we use a 2×2 factorial design, we often graph the means to gain a better understanding of the effects that the independent variables have on the dependent variable.
What happens if two lines are parallel?
If the two lines in the plot are parallel, there is no interaction effect. If the two lines in the plot are not parallel, there is an interaction effect. In the previous plot, the two lines were roughly parallel so there is likely no interaction effect between watering frequency and sunlight exposure.
What is the p-value of the interaction between sunlight and water?
The p-value for the interaction between sunlight and water is .156. Since this is not less than .05, this means there is no interaction effect between sunlight and water.
What is the p-value of sunlight?
The p-value associated with sunlight is .005. Since this is less than .05, this means sunlight exposure has a statistically significant effect on plant growth.
When do interaction effects occur?
Interaction Effects: These occur when the effect that one independent variable has on the dependent variable depends on the level of the other independent variable.
Does sunlight affect plant growth?
For example, this means the effect that sunlight has on plant growth depends on the watering frequency. In other words, sunlight and watering frequency do not affect plant growth independently. Rather, there is an interaction effect between the two independent variables.
What is the second figure in the psychotherapy effect?
The second figure shows a main effect for treatment with psychotherapy performing better (remember the direction of the outcome variable) in all settings than behavior modification. The effect is clearer in the graph on the lower right where treatment levels are used for the lines. Note that in both this and the previous figure the lines in all graphs are parallel indicating that there are no interaction effects.
What is incomplete factorial design?
One of the most common uses of incomplete factorial design is to allow for a control or placebo group that receives no treatment. In this case, it is actually impossible to implement a group that simultaneously has several levels of treatment factors and receives no treatment at all. So, we consider the control group to be its own cell in an incomplete factorial rubric (as shown in the figure). This allows us to conduct both relative and absolute treatment comparisons within a single study and to get a fairly precise look at different treatment combinations.
How many levels are there in setting factor?
Note that the setting factor in this example has three levels.
Can factorial design be cumbersome?
It’s clear that factorial designs can become cumbersome and have too many groups even with only a few factors. In much research, you won’t be interested in a fully-crossed factorial design like the ones we’ve been showing that pair every combination of levels of factors. Some of the combinations may not make sense from a policy or administrative perspective, or you simply may not have enough funds to implement all combinations. In this case, you may decide to implement an incomplete factorial design. In this variation, some of the cells are intentionally left empty – you don’t assign people to get those combinations of factors.
Is day treatment the best?
Now, let’s look at a few of the possible interaction effects. In the first case, we see that day treatment is never the best condition. Furthermore, we see that psychotherapy works best with inpatient care and behavior modification works best with outpatient care.
Is day treatment better than outpatient treatment?
It’s clear that inpatient treatment works best, day treatment is next best, and outpatient treatment is worst of the three. It’s also clear that there is no difference between the two treatment levels (psychotherapy and behavior modification).

A Simple Example
The Null Outcome
- Let’s begin by looking at the “null” case. The null case is a situation where the treatments have no effect. This figure assumes that even if we didn’t give the training we could expect that students would score a 5 on average on the outcome test. You can see in this hypothetical case that all four groups score an average of 5 and therefore the row and column averages must be 5. You c…
The Main Effects
- A main effect is an outcome that is a consistent difference between levels of a factor. For instance, we would say there’s a main effect for setting if we find a statistical difference between the averages for the in-class and pull-out groups, at all levelsof time in instruction. The first figure depicts a main effect of time. For all settings, the 4 hour/week condition worked better than the …
Interaction Effects
- If we could only look at main effects, factorial designs would be useful. But, because of the way we combine levels in factorial designs, they also enable us to examine the interaction effects that exist between factors. An interaction effectexists when differences on one factor depend on the level you are on another factor. It’s important to recognize that an interaction is between factors, …
Summary
- Factorial design has several important features. First, it has great flexibility for exploring or enhancing the “signal” (treatment) in our studies. Whenever we are interested in examining treatment variations, factorial designs should be strong candidates as the designs of choice. Second, factorial designs are efficient. Instead of conducting a se...