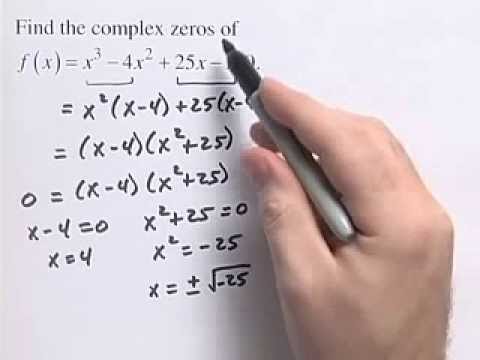
Complex numbers are the numbers that are expressed in the form of a+ib where, a,b are real numbers and ‘i’ is an imaginary number called “iota”. The value of i = (√-1). For example, 2+3i is a complex number, where 2 is a real number (Re) and 3i is an imaginary number (Im).
What are the rules of complex numbers?
- To divide a complex number a+ib by c+id, multiply the numerator and denominator of the fraction a+ib/c+id by c−id and simplify.
- The conjugate of the complex z = a+ib is a−ib.
- The modulus of the complex number z = a+ib is |z| = √ (a 2 + b 2)
What are real numbers in Algebra 2?
Real numbers are the set of all numbers that can be expressed as a decimal or that are on the number line. Real numbers have certain properties and different classifications, including natural, whole, integers, rational and irrational. real numbers natural counting whole integer rational irrational. What we're going to talk about now is just different classifications of numbers.
What are the prerequisites for Algebra 2?
Prerequisites: Minimum B- in the 1st semester and 3rd quarter of Algebra 2/Trigonometry Honors or a minimum A- in the 1st semester and 3rd quarter of Algebra 2. Any student who is not coming from a prior honors math course taken in person at JSerra will be required to take and pass the Honors Math Placement Test.
What are the operations of complex numbers?
Operations with Complex Numbers. To add two complex numbers , add the real part to the real part and the imaginary part to the imaginary part. ( a + b i) + ( c + d i) = ( a + c) + ( b + d) i. Example 1: ( 2 + 7 i) + ( 3 − 4 i) = ( 2 + 3) + ( 7 + ( − 4)) i = 5 + 3 i. To subtract two complex numbers, subtract the real part from the real part ...
What is a complex number in math?
Complex numbers are numbers that consist of two parts — a real number and an imaginary number. Complex numbers are the building blocks of more intricate math, such as algebra. They can be applied to many aspects of real life, especially in electronics and electromagnetism.
What are complex numbers and example?
Complex numbers are the numbers that are expressed in the form of a+ib where, a,b are real numbers and 'i' is an imaginary number called “iota”. The value of i = (√-1). For example, 2+3i is a complex number, where 2 is a real number (Re) and 3i is an imaginary number (Im).
What is a complex root Algebra 2?
Complex roots are the imaginary root of quadratic or polynomial functions. These complex roots are a form of complex numbers and are represented as α = a + ib, and β = c + id. The quadratic equation having a discriminant value lesser than zero (D<0) have imaginary roots, which are represented as complex numbers.
How do you identify a complex number?
A complex number is expressed in standard form when written a+bi where a is the real part and bi is the imaginary part. For example, 5+2i is a complex number. So, too, is 3+4√3i. Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number.
What is not a complex number?
In order for a + bi to include the number i, b cannot be equal to zero. Therefore, a non-real complex number is a number of the form a + bi, where b ≠ 0.
Is every real number is a complex number?
From the second definition, we can conclude that any real number is also a complex number. In addition, there can be complex numbers that are neither real nor imaginary, like 4 + 2 i 4+2i 4+2i4, plus, 2, i.
How do you solve complex and roots?
Solving Quadratic Equations with Complex Roots Step 1: Identify a, b, and c in the quadratic equation ax2+bx+c=0 a x 2 + b x + c = 0 . Step 2: Substitute the values for a, b, and c into the quadratic formula. Step 3: Simplify the expression, remembering that √−k=√ki − k = k i for a positive constant k.
How do you solve complex equations?
0:002:06Solving Equations With Complex Numbers - YouTubeYouTubeStart of suggested clipEnd of suggested clipConsider the equation 8 plus 15i is equal to 2x plus 3y times i what is the value of x and what isMoreConsider the equation 8 plus 15i is equal to 2x plus 3y times i what is the value of x and what is the value of y. In order to solve. It.
What are real and complex roots?
A real root to an equation is a real number. A complex root to an equation is an imaginary root represented as complex numbers.
How do you solve complex numbers step by step?
Step 1: Multiply the complex numbers in the same manner as polynomials. ... Step 2: Simplify the expression. ... Step 3: Write the final answer in standard form.Step 1: Multiply the complex numbers in the same manner as polynomials.Step 2: Simplify the expression.Step 3: Write the final answer in standard form.More items...•
What is 5 as a complex number?
Either Part Can Be ZeroComplex NumberReal PartImaginary Part3 + 2i32550−6i0−6
How do you simplify a complex number?
0:085:56Simplifying Complex Numbers - YouTubeYouTubeStart of suggested clipEnd of suggested clipI to the fourth is basically i squared times i squared. And i squared is negative one negative oneMoreI to the fourth is basically i squared times i squared. And i squared is negative one negative one times negative one is one. So i to the fourth is one make sure you know these four values.
Where are complex numbers used in real life?
Complex numbers in Real life Complex number is used in Electromagnetism. Complex number is used to simplify the unknown roots if roots are not real for quadratic equations. Complex numbers are used in computer science engineering. Complex number is used in mechanical and civil engineering.
What kind of number is 4i?
So, the square root of -16 is 4i. As a double check, we can square 4i (4*4 = 16 and i*i =-1), producing -16. All negative square roots are called "imaginary numbers" (now you know where that letter 'i' comes from).
Is 3i a complex number?
Remember that a complex number has the form a + bi. You need to figure out what a and b need to be. Since −3i is an imaginary number, it is the imaginary part (bi) of the complex number a + bi. This imaginary number has no real parts, so the value of a is 0....Imaginary Numbers3i (b = 3)−672i (b = −672)(b = )(b = )
What are complex numbers used for?
Complex numbers are used in electrical engineering all the time, because Fourier transforms are used in understanding oscillations that occur both in alternating current and in signals modulated by electromagnetic waves.
Which two complex numbers are equal?
Two complex numbers z1 = a + bi and z2 = c + di are said to be equal if these two conditions are satisfied.
How to divide a complex number by another?
To divide a complex number by another, set up the division problem as a fraction and rationalize the denominator. The fact i2 = – 1 is then applied to simplify the expressions.
What is ans in math?
Ans: A complex number has a real part, an imaginary part and an imaginary unit.
What is the multiplicative identity of a complex number?
Multiplicative Identity: A complex number with 1 as the real and 0 as the imaginary parts zero is known as the additive identity. That is, for any complex number z, there exists 1 = 1 + 0i such that z ⋅ 1 = 1 ⋅ z = z
What is the standard form of a complex number?
The standard form of a complex number has a real number part, an imaginary part, and an imaginary unit. So, a complex number looks like,
What is the symbol for a complex number?
Every complex number is a combination of real and imaginary numbers. The standard symbol used for the set of complex numbers is C. It is customary to use z to denote a complex variable. The real and imaginary parts are often represented using lowercase letters such as a, b, c, d, x, y etc.
What is the property of subtraction?
Subtraction of a complex number from another is nothing but the addition of a negative number. That is, for the complex numbers z1 and z2, z1– z2 = z1 + (– z2). Therefore, all the properties of addition hold for subtraction as well.
What is a complex number?
Defining complex numbers. A complex number is any number that can be written as , where is the imaginary unit and and are real numbers. is called the part of the number, and is called the part of the number. The table below shows examples of complex numbers, with the real and imaginary parts identified. Some people find it easier ...
What is the backbone of the number system?
The backbone of this new number system is the number , also known as the imaginary unit.
Is a complex number a real number?
No BUT --- ALL REAL numbers ARE COMPLEX numbers. It just so happens that many complex numbers have 0 as their imaginary part. When 0 is the imaginary part then the number is a real number, and you might think of a real number as a 1-dimensional number.
Is a real number an imaginary number?
Real numbers and imaginary numbers are both complex numbers. Imaginary numbers can be thought of as complex numbers of the form a + bi where a = 0. 0 is a complex number where a and b are 0, so since a = 0 0 is an imaginary number. 3 comments.
Is 0 a real number?
If we define a pure real number as a complex number whose imaginary component is 0i, then 0 is a pure real number.
Can complex numbers be real?
In addition, there can be complex numbers that are neither real nor imaginary, like .
Can complex numbers solve polynomials?
From a purely mathematical standpoint, one cool thing that complex numbers allow us to do is to solve any polynomial equation. For example, the polynomial equation does not have any real solutions nor any imaginary solutions. However, it does have two complex number solutions. These are and .
How To
Given an imaginary number, express it in the standard form of a complex number.
Plotting a Complex Number on the Complex Plane
We cannot plot complex numbers on a number line as we might real numbers. However, we can still represent them graphically. To represent a complex number, we need to address the two components of the number.
Complex Plane
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis, as shown in Figure 3.
Adding and Subtracting Complex Numbers
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and then combine the imaginary parts.
Multiplying Complex Numbers
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Dividing Complex Numbers
Dividing two complex numbers is more complicated than adding, subtracting, or multiplying because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator to write the answer in standard form a + b i. a + b i.
The Complex Conjugate
The complex conjugate of a complex number a + b i a + b i is a − b i. a − b i. It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.
What is a complex number?
What are complex numbers? A complex number can be written in the form a + b i where a and b are real numbers (including 0) and i is an imaginary number. Therefore a complex number contains two 'parts': one that is real. and another part that is imaginary.
How to graph complex numbers?
How do you graph complex numbers? 1 On this plane, the imaginary part of the complex number is measured on the 'y-axis', the vertical axis; 2 the real part of the complex number goes on the 'x-axis' , the horizontal axis;
Is a complex an imaginary part?
note: Even though complex have an imaginary part, there are actually many real life applications of these "imaginary" numbers including oscillating springs and electronics.
What is the standard form of a complex number?
The standard form of a complex number is. where a a and b b are real numbers and they can be anything, positive, negative, zero, integers, fractions, decimals, it doesn’t matter. When in the standard form a a is called the real part of the complex number and b b is called the imaginary part of the complex number.
What is the conjugate of a complex number?
The conjugate of the complex number a +bi a + b i is the complex number a−bi a − b i. In other words, it is the original complex number with the sign on the imaginary part changed. Here are some examples of complex numbers and their conjugates.
What is the rule of thumb when dealing with square roots of negative numbers?
So, there is a general rule of thumb in dealing with square roots of negative numbers. When faced with them the first thing that you should always do is convert them to complex number. If we follow this rule we will always get the correct answer.
Can you multiply polynomials?
Next let’s take a look at multiplication. Again, with one small difference, it’s probably easiest to just think of the complex numbers as polynomials so multiply them out as you would polynomials. The one difference will come in the final step as we’ll see.
Can we break up products under a square root?
In other words, we can break up products under a square root into a product of square roots provided both numbers are positive.
Does the conjugate of a real number change?
Notice that the conjugate of a real number is just itself with no changes.
Is the denominator a pure imaginary number?
This one is a little different from the previous ones since the denominator is a pure imaginary number. It can be done in the same manner as the previous ones, but there is a slightly easier way to do the problem.
What is a complex number?
The complex number is basically the combination of a real number and an imaginary number. The complex number is in the form of a+ib, where a = real number and ib = imaginary number. Also, a,b belongs to real numbers and i = √-1.
How to divide a complex number?
To divide the complex number, multiply the numerator and the denominator by its conjugate. The conjugate of the complex number can be found by changing the sign between the two terms in the denominator value. Then apply the FOIL method to simplify the expression.
What is the result of the multiplication of two complex numbers and its conjugate value?
The result of the multiplication of two complex numbers and its conjugate value should result in a complex number and it should be a positive value.
What is the square of an imaginary number?
An imaginary number is usually represented by ‘i’ or ‘j’, which is equal to √-1. Therefore, the square of the imaginary number gives a negative value.
What happens when the sum of two complex numbers is real?
If the sum of two complex number is real, and also the product of two complex number is also real, then these complex numbers are conjugate to each other.
What does the symbol i mean in math?
We denote √-1 with the symbol ‘i’, which denotes Iota (Imaginary number).
What is the absolute value of a real number?
The absolute value of a real number is the number itself. The absolute value of x is represented by modulus, i.e. |x|. Hence, the modulus of any value always gives a positive value, such that;
What is complex number?
Complex numbers are the sum of a real and an imaginary number, represented as a + bi. Using the complex plane, we can plot complex numbers similar to how we plot a coordinate on the Cartesian plane.
How to find the conjugate of a complex?
To find the complex conjugate, simply flip the sign on the imaginary part. For example, the complex conjugate of (1–4 i) is (1+4 i ).
How to add points in math?
To add these points, simply stack one on top of the other. Since addition is commutative, it doesn’t matter which way we stack them.
Does multiplying by a real number scale the value?
In general, we know multiplying by a real number scales the value, and we learned in the last post that multiplying by i rotates a value by 90˚ counter clockwise, but how about this?
Is the imaginary number in the denominator confusing?
Truthfully, it’s confusing and there isn’t a great explanation for it. Wouldn’t it be nice if we could get rid of the imaginary number in the denominator??

Complex Numbers: Definition
Addition of Two Complex Numbers
Subtraction of Two Complex Numbers
Multiplication of Two Complex Numbers
Division of Two Complex Numbers
Complex Notation of The Square Root of A Negative Real Number
Solved Examples – Algebra of Complex Numbers
Summary
Frequently Asked Questions (FAQs): Algebra of Complex Numbers
- Q.1. What is a complex number in algebra? Ans: A complex number is a combination of real and imaginary numbers. The standard form of a complex number has a real number part, an imaginary part, and an imaginary unit. So, for a complex number \(z = a + bi\) \(a \to \) real part \(b \to \) imaginary part \(i \to \) imaginary unit and \(i = \sqrt { – 1...