What is an example of a conic map?
When a single parallel line has used the distance along the parallels is stretched. Examples of conic maps include equidistant, Albers, and Lambert conformal conic. Pseudoconic Projections are projections with parallels which are circular arcs with common central points.
What is a conic projection in geology?
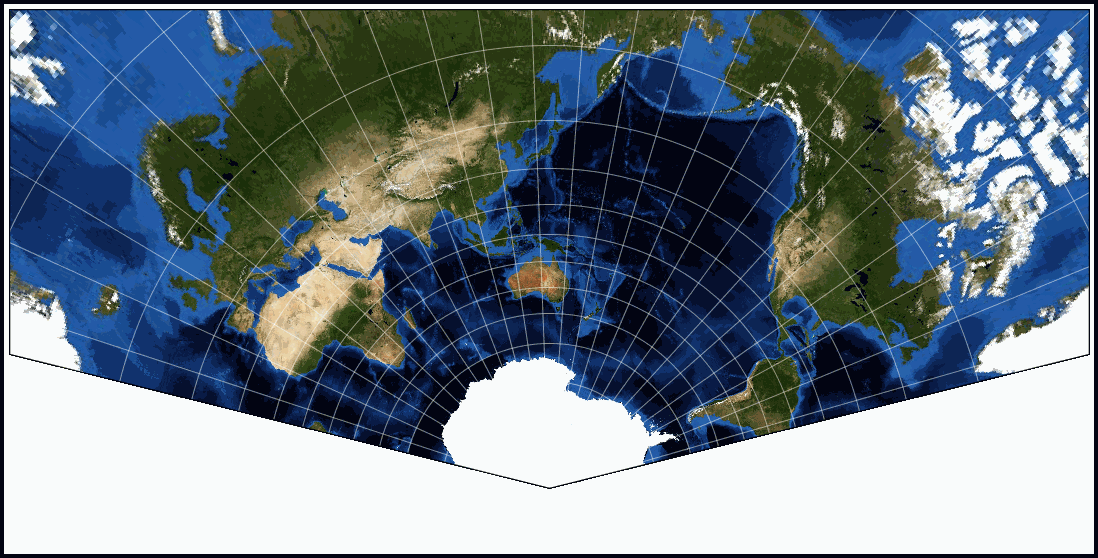
Conic Projections. A conic projection is derived from the projection of the globe onto a cone placed over it. For the normal aspect, the apex of the cone lies on the polar axis of the Earth. If the cone touches the Earth at just one particular parallel of latitude, it is called tangent.
What is conformal conic map projection?
Lambert conformal conic map projection is normally based on two standard parallels, but it can also be defined with a single standard parallel and a scale factor. It is best suited for conformal mapping of land masses extending in an east-to-west orientation at mid-latitudes.
What are the advantages and disadvantages of conic map projection?
The major advantage of the Lambert Conformal Conic map projection is how it retains conformality. Despite how distances are reasonable accurate and retained along standard parallels, it isn’t equal-area as distortion increases away from standard parallels. What are the cons of conic projection?
What is an example of a conic projection?
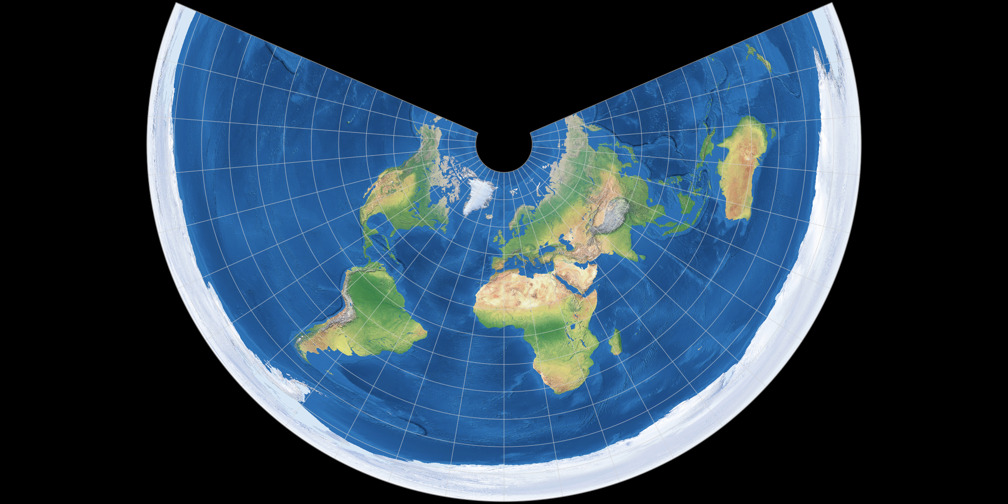
Conic Projection Examples. When you place a cone on the Earth and unwrap it, this results in a conic projection. Some of the popular conic projections are Albers Equal Area Conic and the Lambert Conformal Conic projections.
How is a conic map projection made?
Conic projections are derived from a projection of the globe on a cone drawn with the point above either the North or South Pole and tangent to the Earth at some standard or selected parallel.
What are the advantages or disadvantages of conical projection?
Conical Projections: Pros: These maps are very good for mapping regions that are primarily West-East in dimension like the United States. That is because a cone, when developed, is itself wider than tall. Cons: The basic con is that a single cone cannot show the entire globe.
Do pilots use conic projection?
Pilots use aeronautical charts based on LCC because a straight line drawn on a Lambert conformal conic projection approximates a great-circle route between endpoints for typical flight distances.
What are 4 types of map projections?
What Are The 4 Main Types Of Map projectionsAzimuthal projection.Conic projection.Cylindrical projection.Conventional projection or Mathematical projection.
What are the characteristics of conical projections?
General characteristicsLines of latitude and longitude are intersecting at 90 degrees.Meridians are straight lines.Parallels are concentric circular arcs.Scale along the standard parallel(s) is true.Can have the properites of equidistance, conformality or equal area.The pole is represented as an arc or a point.
Which conic projections are most suitable for maps of mid latitude regions?
The Lambert Conformal Conic is the preferred projection for regional maps in mid-latitudes. In Australia the national mapping agency prefers to use this projection using 18° and 36° South as the two Standard Parallels.
What is the most simple conic projection?
Conic projections. The most simple Conic projection is tangent to the globe along a line of latitude. This line is called the standard parallel. The meridians are projected onto the conical surface, meeting at the apex, or point, of the cone. Parallel lines of latitude are projected onto the cone as rings.
What is the representation of geographic features?
The representation of geographic features depends on the spacing of the parallels. When equally spaced, the projection is equidistant north–south but neither conformal nor equal area. An example of this type of projection is the Equidistant Conic projection. For small areas, the overall distortion is minimal. On the Lambert Conic Conformal projection, the central parallels are spaced more closely than the parallels near the border, and small geographic shapes are maintained for both small-scale and large-scale maps. On the Albers Equal Area Conic projection, the parallels near the northern and southern edges are closer together than the central parallels, and the projection displays equivalent areas.
What is the purpose of cutting off the top of a cone?
In general, the further you get from the standard parallel, the more distortion increases. Thus, cutting off the top of the cone produces a more accurate projection. You can accomplish this by not using the polar region of the projected data. Conic projections are used for midlatitude zones that have an east–west orientation.
Which type of projection has less distortion?
Generally, a Secant project ion has less overall distortion than a Tangent projection. On still more complex Conic projections, the axis of the cone does not line up with the polar axis of the globe. These types of projections are called oblique.
What is azimuthal projection?
An azimuthal projection is a projection of the globe onto a plane. In polar aspect, an azimuthal projection maps to a plane tangent to the Earth at one of the poles, with meridians projected as straight lines radiating from the pole, and parallels shown as complete circles centered at the pole. Azimuthal projections (especially the orthographic) can have equatorial or oblique aspects. The projection is centered on a point, that is either on the surface, at the center of the Earth, at the antipode, some distance beyond the Earth, or at infinity. Most azimuthal projections are not suitable for displaying the entire Earth in one view, but give a sense of the globe. The following figure illustrates azimuthal projection, diagramming it on the left, with an example on the right (orthographic projection, polar aspect).
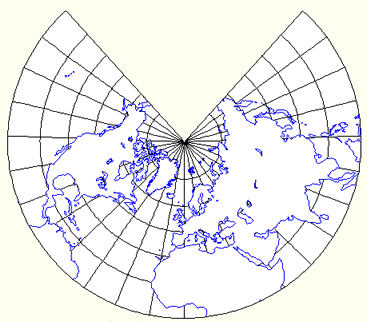
How is conic projection derived?
A conic projection is derived from the projection of the globe onto a cone placed over it. For the normal aspect, the apex of the cone lies on the polar axis of the Earth. If the cone touches the Earth at just one particular parallel of latitude, it is called tangent. If made smaller, the cone will intersect the Earth twice, in which case it is called secant . Conic projections often achieve less distortion at mid- and high latitudes than cylindrical projections. A further elaboration is the polyconic projection, which deploys a family of tangent or secant cones to bracket a succession of bands of parallels to yield even less scale distortion. The following figure illustrates conic projection, diagramming its construction on the left, with an example on the right (Albers equal-area projection, polar aspect).
How to make a cylindrical projection?
A cylindrical projection is produced by wrapping a cylinder around a globe representing the Earth . The map projection is the image of the globe projected onto the cylindrical surface, which is then unwrapped into a flat surface. When the cylinder aligns with the polar axis, parallels appear as horizontal lines and meridians as vertical lines. Cylindrical projections can be either equal-area, conformal, or equidistant. The following figure shows a regular cylindrical or normal aspect orientation in which the cylinder is tangent to the Earth along the Equator and the projection radiates horizontally from the axis of rotation. The projection method is diagrammed on the left, and an example is given on the right (equal-area cylindrical projection, normal/equatorial aspect).
What does a parallel look like when it aligns with the polar axis?
When the cylinder aligns with the polar axis, parallels appear as horizontal lines and meridians as vertical lines. Cylindrical projections can be either equal-area, conformal, or equidistant.
Which type of projections have less distortion?
Conic projections often achieve less distortion at mid- and high latitudes than cylindrical projections. A further elaboration is the polyconic projection, which deploys a family of tangent or secant cones to bracket a succession of bands of parallels to yield even less scale distortion.
What are map projections?
These are based on the types of geometric shapes that are used to transfer features from a sphere or spheroid to a plane. Map projections are based on developable surfaces , and the three traditional families consist of cylinders, cones, and planes. They are used to classify the majority of projections, including some that are not analytically (geometrically) constructed. In addition, a number of map projections are based on polyhedra. While polyhedral projections have interesting and useful properties, they are not described in this guide.
Do pseudocylindrical projections have straight lines?
However, they do resemble cylindrical projections, with straight and parallel latitude lines, and can have equally spaced meridians, but meridians are curves, not straight lines. Pseudocylindrical projections can be equal-area, but are not conformal or equidistant. Some widely-used pseudocylindrical map projections are.
What is cylindrical projection?
A cylindrical projection is any projection in which the meridians are mapped to parallel spaced vertical lines and latitudes are mapped to horizontal lines. The projections stretch from east to west according to their geometric constructions and are the same at any chosen latitude. Cylindrical projections are distinguished from each other by the north to south stretching denoted by φ. The north to south stretching equals east to west but grows with latitude faster than east to west stretching in the case of central cylindrical projection. Mercator projection is an example of cylindrical projection which became a standard map projection because of its ability to represent lines of steady course. Mercator distorts the size of geographical objects because its linear scale increases with the increase in latitude. The distortion caused by the Mercator distorts the perception of the entire planet by exaggerating the areas laying far from the equator.
What is the scaling of a pseudocylindrical projection?
The scaling of the pseudocylindrical projections are straight along the central meridian and also along the parallels. On a pseudocylindrical map, points further from the equator have higher latitudes than other points, preserving the north-south relationship. Pseudocylindrical projections include sinusoidal with same horizontal and vertical scales.
Why are map projections important?
Map projections are important in creating maps with map projections distorting the surface in some way. Some of the distortions on the maps are acceptable while other distortions are not acceptable depending on the purpose of the map. The map projection is classified depending on the type of projection surface on which the globe is projected ...
What is distortion in maps?
Map projections without distortions would represent the correct distance, direction, shapes, and areas on a map. However, map projections have distortions which depend largely on the size of the area being mapped. Scale distortions on maps are shown on the map by an ellipse of distortion or using scale factor which is the ratio of the scale at a given point to the true scale. Distortions on maps of countries or cities are not evident to the eye and can only be identified when computing distances and areas.
Why is the Robinson projection not equal area?
The projection is neither equal-area nor conformal because of the compromise to show the whole planet. The meridians of the Robinson projection curves are gently stretching the poles into long lines.
How does the mercator distort the size of geographical objects?
Mercator distorts the size of geographical objects because its linear scale increases with the increase in latitude. The distortion caused by the Mercator distorts the perception of the entire planet by exaggerating the areas laying far from the equator.
Which projection is an example of a cylindrical projection?
The north to south stretching equals east to west but grows with latitude faster than east to west stretching in the case of central cylindrical projection. Mercator projection is an example of cylindrical projection which became a standard map projection because of its ability to represent lines of steady course.
What is a Map Projection?
A map projection is a way of representing the curved surface of the Earth on a flat surface. There are many different map projections, each with its own advantages and disadvantages.
Cartography and map projection
In cartography, a map projection is the systematic conversion of the latitudes and longitudes of locations on the surface of a sphere or an ellipsoid into locations on a plane. Map projections are necessary for creating maps.
What is lateral meridians?
The lateral meridians are semicircles which give the projection a nice rounded shape and smooth corners where the lateral meridians meet the pole lines. Projection was introduced by Max Eckert in 1906. It is available in ArcGIS Pro 1.0 (ArcGIS 8.0) and later. Eckert III compromise map projection centered on Greenwich.
What is the Eckert I?
The Eckert I is a compromise pseudocylindrical map projection with rectilinear meridians and odd appearance. Projection is simple, but it has no practical use besides making a world map with an unusual shape. Projection was introduced by Max Eckert in 1906. It is available in ArcGIS Pro 1.0 (ArcGIS 8.0) and later.
What is Berghaus star projection?
The Berghaus star projection uses the azimuthal equidistant projection for the central hemisphere. The other half of the world is split into five triangular pieces, forming a star around the circular center. Usually centered at the North Pole, it can minimize breaks in land masses. The Association of American Geographers (AAG) incorporated a version of the Berghaus star projection into the logo in 1911. The projection was developed by Hermann Berghaus in 1879. Equations for an ellipsoid of revolution were developed at Esri. It is available in ArcGIS Pro 1.0 (ArcGIS 10.0) and later.
What is the polar aspect of the projection?
Although all aspects are possible (equatorial, polar, and oblique), the one used most commonly is the polar aspect, in which all meridians and parallels are divided equally to maintain the equidistant property. It is believed that the projection was first used by Egyptians for star charts. It is available in ArcGIS Pro 1.0 (ArcGIS 8.0) and later.
How many sides does a cube have?
The Cube is a faceted projection consisting of six square sides, one for each pole and four along the equator centered at 135°and 45° West, 45° and 135° East meridians. It can be folded into a cube. Areas between 45° North and 45° South are projected with the Plate Carrée projection. The projection is available in ArcGIS Pro 1.0 (ArcGIS 9.0) and later.
What is the Behrmann projection?
The Behrmann projection is a case of the cylindrical equal-area map projection with standard parallels set at 30° North and South. Due to its equal-area property, it highly compresses polar regions. The projection was introduced by Walter Behrmann in 1910. It is available in ArcGIS Pro 1.0 (ArcGIS 8.0) and later.
What is an aspect adaptive projection?
The aspect-adaptive cylindrical projection is a compromise map projection that adjusts the parallels to the height-to-width (aspect) ratio of an available canvas. It supports any ratio between 0.3 and 1. The projection was developed by Bernhard Jenny, Bojan Šavrič, and Tom Patterson in 2014. It is available in ArcGIS Pro 2.1 (ArcGIS 10.6) and later.