what is a line tangent to two circles

Full Answer

How to determine if a line is tangent in a circle?

Answer: The properties are as follows: The tangent line never crosses the circle, it just touches the circle. At the point of tangency, it is perpendicular to the radius. A chord and tangent form an angle and this angle is the same as that of tangent inscribed on the opposite side of the chord. From the same external point, the tangent segments to a circle are equal.

Can two circles be tangent at the same point?

Two circles are tangent to each other if they have only one common point. Two circles that have two common points are said to intersect each other. Two circles can be externally tangent if the circles are situated outside one another and internally tangent if one of them is situated inside the other.

How to find equations of tangent lines and normal lines?

• Substitute the given x-value into the function to find the y-value or point.
• Calculate the first derivative of f (x).
• Plug the ordered pair into the derivative to find the slope at that point.
• Substitute both the point and the slope from steps 1 and 3 into point-slope form to find the equation for the tangent line.

How many points does a tangent line touch a circle?

A tangent is a line (or line segment) that intersects a circle at exactly one point. To do that, the tangent must also be at a right angle to a radius (or diameter) that intersects that same point. In our crop circle U, if we look carefully, we can see a tangent line off to the right, line segment FO.

How do you find the equation of a tangent to two circles?

A line with equation ax+y+c=0 is tangent to a circle iff its distance from the center of the circle is equal to the radius of the circle, so you get the system of equations: {|2a+c|=3√a2+1|5a+4+c|=2√a2+1.

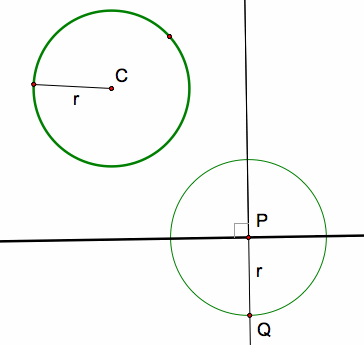
What does it mean when a line is tangent to a circle?

A tangent line is a line that intersects a circle at one point. Such a line is said to be tangent to that circle. The point at which the circle and the line intersect is the point of tangency.

How do you explain tangent in math?

In Geometry, the tangent is defined as a line touching circles or an ellipse at only one point. Suppose a line touches the curve at P, then the point “P” is called the point of tangency. In other words, it is defined as the line which represents the slope of a curve at that point.

Can two circles be tangent to the same line at the same point?

When two circles touches one another at exactly one point, then we say that the two circles are tangent to one another. In this case, the two circles share a common tangent line at the tangent point.

What does it mean if something is tangent to something?

Tangent is mainly a mathematical term, meaning a line or plane that intersects a curved surface at exactly one point. The non-mathematical meaning of tangent comes from this sense of barely touching something: when a conversation heads off on a tangent, it's hard to see how or why it came up.

What does it mean if something is tangent?

Definition of tangent (Entry 1 of 2) 1 : an abrupt change of course : digression the speaker went off on a tangent. 2a : the trigonometric function that for an acute angle is the ratio between the leg opposite to the angle when it is considered part of a right triangle and the leg adjacent.

What does it mean when something is tangent to another?

Tangent is something or a thought that touches but doesn't intersect, or is irrelevant. An example of a tangent is someone talking about a problem at work and then suddenly starts talking about something that happened to them in elementary school.

What is tangent of a circle with example?

A tangent to a circle is a straight line which touches the circle at only one point. This point is called the point of tangency. The tangent to a circle is perpendicular to the radius at the point of tangency. In the circle O , ↔PT is a tangent and ¯OP is the radius.

How many tangents are there in a circle?

For two circles, there are generally four distinct lines that are tangent to both ( bitangent) – if the two circles are outside each other – but in degenerate cases there may be any number between zero and four bitangent lines; these are addressed below. For two of these, the external tangent lines, the circles fall on the same side of the line; for the two others, the internal tangent lines, the circles fall on opposite sides of the line. The external tangent lines intersect in the external homothetic center, whereas the internal tangent lines intersect at the internal homothetic center. Both the external and internal homothetic centers lie on the line of centers (the line connecting the centers of the two circles), closer to the center of the smaller circle: the internal center is in the segment between the two circles, while the external center is not between the points, but rather outside, on the side of the center of the smaller circle. If the two circles have equal radius, there are still four bitangents, but the external tangent lines are parallel and there is no external center in the affine plane; in the projective plane, the external homothetic center lies at the point at infinity corresponding to the slope of these lines.

How to draw tangent lines?

Another method to construct the tangent lines to a point P external to the circle using only a straightedge : 1 Draw any three different lines through the given point P that intersect the circle twice. 2 Let#N#A 1 , A 2 , B 1 , B 2 , C 1 , C 2 {displaystyle A_ {1},A_ {2},B_ {1},B_ {2},C_ {1},C_ {2}}#N#be the six intersection points, with the same letter corresponding to the same line and the index 1 corresponding to the point closer to P. 3 Let D be the point where the lines#N#A 1 B 2 {displaystyle A_ {1}B_ {2}}#N#and#N#A 2 B 1 {displaystyle A_ {2}B_ {1}}#N#intersect, 4 Similarly E for the lines#N#B 1 C 2 {displaystyle B_ {1}C_ {2}}#N#and#N#B 2 C 1 {displaystyle B_ {2}C_ {1}}#N#. 5 Draw a line through D and E. 6 This line meets the circle at two points, F and G. 7 The tangents are the lines PF and PG.

How to find angle of tangent line?

Geometrically this corresponds to computing the angle formed by the tangent lines and the line of centers, and then using that to rotate the equation for the line of centers to yield an equation for the tangent line. The angle is computed by computing the trigonometric functions of a right triangle whose vertices are the (external) homothetic center, a center of a circle, and a tangent point; the hypotenuse lies on the tangent line, the radius is opposite the angle, and the adjacent side lies on the line of centers.

How to construct bitangent lines?

The bitangent lines can be constructed either by constructing the homothetic centers, as described at that article, and then constructing the tangent lines through the homothetic center that is tangent to one circle, by one of the methods described above. The resulting line will then be tangent to the other circle as well. Alternatively, the tangent lines and tangent points can be constructed more directly, as detailed below. Note that in degenerate cases these constructions break down; to simplify exposition this is not discussed in this section, but a form of the construction can work in limit cases (e.g., two circles tangent at one point).

What is the difference between secant and tangent lines?

For comparison, secant lines intersect a circle at two points, whereas another line may not intersect a circle at all. This property of tangent lines is preserved under many geometrical transformations, such as scalings, rotation, translations, inversions, and map projections. In technical language, these transformations do not change the incidence structure of the tangent line and circle, even though the line and circle may be deformed.

How many bitangents are there in a projective plane?

If the two circles have equal radius, there are still four bitangents, but the external tangent lines are parallel and there is no external center in the affine plane; in the projective plane, the external homothetic center lies at the point at infinity corresponding to the slope of these lines.

What is a tangential polygon?

A tangential polygon is a polygon each of whose sides is tangent to a particular circle, called its incircle. Every triangle is a tangential polygon, as is every regular polygon of any number of sides; in addition, for every number of polygon sides there are an infinite number of non- congruent tangential polygons.

How many common tangents are there in two circles?

In most cases, two circles have four common tangents.

How many tangents does a circle have?

In most cases, two circles have four common tangents. If the circles are tangent , then they will have three common tangents, but this can be understood as a degenerate case: as if the two tangents coincided. Moreover, the algorithm described below will work in the case when one or both circles have zero radius: in this case there will be, ...

Can you find tangents to a circle passing through a given point?

all such lines that touch both circles simultaneously. The described algorithm will also work in the case when one (or both) circles degenerate into points. Thus, this algorithm can also be used to find tangents to a circle passing through a given point.

How to draw a tangent line in AutoCAD?

Simplest way to draw a line tangent to two circles is: 1:click line. 2:type 'tan' and press enter. 3:click on Circle 1. 4:type 'tan' again and press enter. 5:click on Circle 2. Will work for any version AutoCAD. Try it, you'll thank me later.

What is a circle in geometry?

A circle is the locus of a cursor, starting and ending at the same point on a plane in model space or in layout such that its distance from a given coordinates (X,Y) is always constant.

Do you have to do the second tan in Snap?

Thank you and welcome. This had been answered about 2 years ago. Actually you don't have to do the second "tan"; just click on the circle where the "tan" symbol appears. That is as long as tan has been added to the snap list.

What is a tangent of a circle?

Tangent of a Circle: We see many circular objects in our surroundings—for example, a circular clock, coins, frisbee, wheels of a train on the track, etc. A line touching the boundary of a circle at exactly one point is known as a tangent of the circle.

How many tangents can be drawn on a circle?

Now, take a point P on the circle and draw tangents through this point. We observe that only one tangent can be drawn at any point on the circle.

How to draw tangent lines?

Consider a circle with a centre O and draw two lines perpendicular to the circle’s radius from two distinct points on the circle. That perpendicular lines are called the tangent to the circle.

What is the perpendicular line called?

That perpendicular line called the tangent to the circle. Case 2: To draw two tangent lines. Consider a circle with a centre O and draw two lines perpendicular to the circle’s radius from two distinct points on the circle. That perpendicular lines are called the tangent to the circle.

Which theorem states that the tangent at any point of a circle is perpendicular to?

Theorem 1: The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Which theorem states that a line perpendicular to the radius at its point on the circle is?

Theorem 2: A line perpendicular to the radius at its point on the circle is a tangent to the circle.

What is the point of contact in a circle?

Definition: A tangent to a circle is a line that touches the circle at only one point. And the point of contact is known as the point of tangency. Here, A B is the centre of the circle, and P is the point of tangency.

How many tangents are there in a circle?

As shown below, there are two such tangents, the other one is constructed the same way but on the bottom half of the circles.

What is tangent in geometry?

Tangents through an external point. Tangents to two circles (external) Tangents to two circles (internal) Incircle of a triangle. Focus points of a given ellipse.

What is PJ in math?

1. PJ is a tangent to the inner circle O at J. By construction. See Constructing the tangent through an external point for method and proof. 2. FP is parallel to LJ. By construction. See Constructing a parallel (angle copy method) for method and proof. 3.

Is tangent FL parallel to PJ?

The desired tangent FL is parallel to PJ and offset from it by JL. Since PJLF is a rectangle, we need the best way to construct this rectangle. The method used here is to construct PF parallel to OL using the "angle copy" method as shown in Constructing a parallel through a point

What is a tangent to a circle?

Tangent to a Circle. A line that touches the circle at a single point is known as a tangent to a circle. The point where tangent meets the circle is called point of tangency. The tangent is perpendicular to the radius of the circle, with which it intersects. Tangent can be considered for any curved shapes.

How many tangents can be found at a point to a circle?

There can be only one tangent at a point to circle. Point of tangency is the point at which tangent meets the circle. Now, let’s prove tangent and radius of the circle are perpendicular to each other at the point of contact. Take a point D on tangent AB other than C and join OD.

What is the shortest distance between the centre of circle O and tangent AB?

It can be concluded that OC is the shortest distance between the centre of circle O and tangent AB. Since, the shortest distance between a point and a line is the perpendicular distance between them, OC is perpendicular to AB. From the above discussion, it can be concluded that:

Why should point D lie outside the circle?

Point D should lie outside the circle because; if point D lies inside, then AB will be a secant to the circle and it will not be a tangent. Therefore, OD will be greater than the radius of circle OC. This happens for every point on AB except the point of contact C.

Which theorem states that the tangent to the circle is perpendicular to the radius of the?

Theorem 1: The tangent to the circle is perpendicular to the radius of the circle at the point of contact.

When is a tangent considered?

The tangent is considered only when it touches a curve at a single point or else it is said to be simply a line. Thus, based on the point of tangency and where it lies with respect to the circle, we can define the conditions for tangent as: When point lies inside the circle. When point lies on the circle. When point lies outside the circle.

Is the line containing the radius through the point of contact normal?

We can call the line containing the radius through the point of contact as ‘normal’ to the circle at the point

Overview

In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.

Tangent lines to one circle

Tangent lines to two circles

Tangent lines to three circles: Monge's theorem

Problem of Apollonius

Generalizations

External links