What are the steps for solving a quadratic equation?
What are the 7 steps in solving quadratic equation by completing the square?
- Isolate the number or variable c to the right side of the equation.
- Divide all terms by a (the coefficient of x2, unless x2 has no coefficient).
- Divide coefficient b by two and then square it.
- Add this value to both sides of the equation.
How do you write a quadratic equation?
Writing Quadratic Equations
- Plug in the coordinates for x and y into the general form. Remember y and f (x) represent the same quantity.
- Simplify. (Remember the order of operations)
- Repeat steps 1 & 2 for the other two points.
- Take two equations at a time and eliminate one variable (c works well)
- Then repeat using two equations and eliminate the same variable you eliminated in #4.
Unit/writingquads.html More items...
What are the 3 forms of a quadratic equation?
Well, quadratic equation basically has three different forms and the solution of these forms also vary. The three forms of the quadratic equation include the standard form, vertex form, and the intercept form at last. You have to study each form separately while studying the quadratic equation chapter in your academics.
How do we use quadratic equations in real life?
Uses of quadratic equations in daily life
- Figuring a Profit. Quadratic equations are often used to calculate business profit. ...
- Calculating Room Areas. Whenever construction is taking place, constructors use quadratic equations to determine the area. ...
- Quadratics in sports. ...
- Learning. ...
- Finding a Speed. ...
- A satellite dish. ...
- Military and law enforcement. ...
- Engineering. ...
- Management and clerical work. ...
- Agriculture. ...

What is the 3 example of quadratic equation?
Examples of quadratic equations are: 6x² + 11x – 35 = 0, 2x² – 4x – 2 = 0, 2x² – 64 = 0, x² – 16 = 0, x² – 7x = 0, 2x² + 8x = 0 etc. From these examples, you can note that, some quadratic equations lack the term “c” and “bx.”
What is quadratic equation explain with example?
In math, we define a quadratic equation as an equation of degree 2, meaning that the highest exponent of this function is 2. The standard form of a quadratic is y = ax^2 + bx + c, where a, b, and c are numbers and a cannot be 0. Examples of quadratic equations include all of these: y = x^2 + 3x + 1. y = x^2.
How do you identify a quadratic equation?
0:031:55Identifying Quadratic Equations - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe quadratic equations a quadratic equation is an equation where you have X to the 2nd power andMoreThe quadratic equations a quadratic equation is an equation where you have X to the 2nd power and that's your highest power of X. So y equals x squared would be the most basic quadratic.
What are the 5 examples of quadratic equation?
Examples include:2x² - 64 = 0.x² - 16 = 0.9x² + 49 = 0.-2x² - 4 = 0.4x² + 81 = 0.-x² - 9 = 0.3x² - 36 = 0.6x² + 144 = 0.
Why it is called quadratic equation?
In mathematics, a quadratic is a type of problem that deals with a variable multiplied by itself — an operation known as squaring. This language derives from the area of a square being its side length multiplied by itself. The word "quadratic" comes from quadratum, the Latin word for square.
What is not a quadratic equation?
Examples of NON-quadratic Equations bx − 6 = 0 is NOT a quadratic equation because there is no x2 term. x3 − x2 − 5 = 0 is NOT a quadratic equation because there is an x3 term (not allowed in quadratic equations).
What is the easiest way to learn quadratic equations?
1:1219:55Learn The Quadratic Formula in 10 min - YouTubeYouTubeStart of suggested clipEnd of suggested clipOkay set it equal to zero. Just like this and then you would go ahead and set each of these factorsMoreOkay set it equal to zero. Just like this and then you would go ahead and set each of these factors equal to zero and then you would solve.
Which of the following is not a quadratic equation?
option B is a linear equation, not a quadratic equation.
What is a quadratic equation class 10?
A quadratic equation in the variable x is an equation of the form ax2 + bx + c= 0, where a, b, c are real numbers, a * 0. For example, 2x2 + x – 300 = 0 is a quadratic equation.
What are real life examples of quadratic equations?
Throwing a ball, shooting a cannon, diving from a platform and hitting a golf ball are all examples of situations that can be modeled by quadratic functions. In many of these situations you will want to know the highest or lowest point of the parabola, which is known as the vertex.
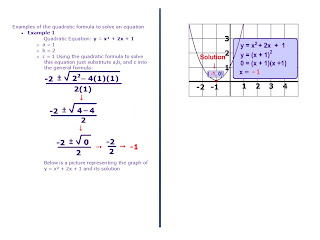
How do you solve quadratic equations examples?
0:424:27Solving Quadratic Equations using the Quadratic Formula - Example 1YouTubeStart of suggested clipEnd of suggested clipSo really all we have to do is just replace all the values in the formula. Being careful with theirMoreSo really all we have to do is just replace all the values in the formula. Being careful with their signs do a little bit of arithmetic. And we'll have our solutions.
What is a quadratic equation?
The polynomial equation whose highest degree is two is called a quadratic equation. The equation is given by ax² + bx + c = 0, where a ≠ 0.
What are the methods to solve a quadratic equation?
There are majorly four methods of solving quadratic equations. They are: Factorisation Using Square roots Completing the square Using quadratic...
Is x 2 – 1 a quadratic equation?
Since the degree of the polynomial is 2, therefore, given equation is a quadratic equation.
What is the solution of x 2 + 4 = 0?
The solution of quadratic equation x 2 – 4 is x = 2 or x = -2.
Write the quadratic equation in the form of sum and product of roots.
If α and β are the roots of a quadratic equation, then; Sum of the roots = α+β Product of the roots = αβ Therefore, the required equation is: x...
What are the solutions to the quadratic equation?
The " solutions " to the Quadratic Equation are where it is equal to zero.
Why is quadratic called quadratic?
The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x2 ).
Does a graph cross the x axis?
The graph does not cross the x-axis. That is why we ended up with complex numbers.
What is quadratic equation?
A quadratic equation is a second-degree equation with one unknown variable. Explore the definition and examples of a quadratic function, the graph of a quadratic equation, when a quadratic equation can have two solutions, and why quadratics are important. Updated: 10/01/2021
What is the standard form of a quadratic equation?
The standard form of a quadratic is y = ax ^2 + bx + c, where a, b, and c are numbers and a cannot be 0.
How many real solutions can a quadratic equation have?
An interesting thing about quadratic equations is that they can have up to two real solutions. Solutions are where the quadratic equals 0. Real solutions mean that these solutions are not imaginary and are real numbers. Imaginary numbers are those numbers with an imaginary part: i.
Which graph of a quadratic function produces the shape of a parabola?
The upwards and downwards curves of the ball produce the shape of a parabola which is the graph of a quadratic function. Hence the motion of the ball can be mathematically modeled using a quadratic function with highest power on the variable being 2.
Does a quadratic function cross the x axis?
Here, the graph of the quadratic function does not cross or touch the x-axis at any point on it. 2. As the ball is shot out of the cannon, it curves upwards and then reaches a maximum height. Following that point in time, the ball begins its descent in a downward curve or path towards the crowd.
Do all quadratics have real solutions?
All quadratics will have two solutions, but not all may be real solutions. If we have less than two real solutions, the other solutions will be imaginary solutions. We can see quadratic functions at work in real life whenever we see a curve. The electrical wires hanging from electrical poles are an example.
What is quadratic equation?
Quadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0. The word " Quadratic " is derived from the word " Quad " which means square. In other words, a quadratic equation is an “ equation of degree 2 .” There are many scenarios where a quadratic equation is used. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy.
What is the first condition for an equation to be a quadratic equation?
The first condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠0) . For writing a quadratic equation in standard form, the x 2 term is written first, followed by the x term, and finally, the constant term is written.
What is the discriminant of a quadratic equation?
The determinant of a quadratic equation ax² + bx + c = 0 is b² - 4ac. The discriminant is referred as D = b² - 4ac. If D > 0 the roots are real and distinct, for D = 0 the roots are equal, and for D < 0 the roots are imaginary complex numbers.
What is the difference between a linear and a quadratic equation?
A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the form ax + b = 0 and a quadratic equation is of the form ax² + bx + c = 0.
How to find the roots of a quadratic equation?
The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. The roots of a quadratic equation are referred to by the symbols alpha (α), and beta (β). These roots of the quadratic equation are also called the zeros of the equation. Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation. And also check out the formulas to find the sum and the product of the roots of the equation.
What is the maximum and minimum value of a quadratic equation?
The maximum and minimum value for the quadratic equation ax 2 + bx + c = 0 can be observed in the below graphs. For positive values of a (a > 0), the quadratic expression has a minimum value at x = -b/2a, and for negative value of a (a < 0), the quadratic expression has a maximum value at x = -b/2a.
How many ways can you solve a quadratic equation?
The four ways of solving a quadratic equation are as follows.
What is quadratic equation?
What is a quadratic equation? A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared. The standard form is ax² + bx + c = 0 with a, b and c being constants, or numerical coefficients, and x being an unknown variable.
What is the equation for quadratic function?
quadratic function - equation expressed as f (x) = a (x - h)2 which is used to graph a parabola
How to learn quadratics?
The easiest way to learn quadratic equations is to start in standard form. While not every quadratic equation you see will be in this form, it's still helpful to see examples. Keep in mind that the first constant a cannot be a zero. Examples of the standard form of a quadratic equation (ax² + bx + c = 0) include:
What is coefficient in math?
coefficient - the number that multiplies the variable by a specific amount (the 4 in 4x)
Can quadratic equations lack constant term?
Quadratic equations can also lack the constant term, or c. For example:
Is every quadratic equation a standard form?
As you develop your algebra skills, you'll find that not every quadratic equation is in the standard form. Check out examples of several different instances of non-standard quadratic equations.
What is the Quadratic Formula?
You can always find the solutions of any quadratic equation using the quadratic formula. The quadratic formula is:
Why is quadratic equation important?
Quadratic equations are actually used every day. They can be used to calculate areas, formulate the speed of an object, and even to determine a product's profit. It is important that you know how to find solutions for quadratic equations using the Quadratic Formula.
What does the word "square" mean in math?
But the origin of the word means “to make square,” as in length times width. In math, the meaning of square is an exponent to the second degree. These exponents are powers of 2. So a quadratic polynomial has as its highest value something to the second degree; something squared.
What is the meaning of square in polynomials?
But the origin of the word means “to make square,” as in length times width. In math, the meaning of square is an exponent to the second degree. These exponents are powers of 2 2:
Can you use the quadratic formula to solve quadratic equations?
You can use this formula to solve quadratic equations. Or, if your equation factored, then you can use the quadratic formula to test if your solutions of the quadratic equation are correct.
Can a graphing calculator be used to calculate the precision of a quadratic formula?
Graphing calculators will probably not be equal to the precision of the Quadratic Formula. Use the calculator to verify the rounded results, but expect them to be slightly different.
When are quadratic equations needed?
Quadratic equations are also needed when studying lenses and curved mirrors.
How to get rid of fractions?
First, get rid of the fractions by multiplying through by (x-2)(x+2):
Graphing
You can graph a Quadratic Equation using the Function Grapher, but to really understand what is going on, you can make the graph yourself. Read On!
But Why?
The wonderful thing about this new form is that h and k show us the very lowest (or very highest) point, called the vertex:

Standard Form
Have A Play with It
Hidden Quadratic Equations!
How to Solve them?
About The Quadratic Formula
Complex Solutions?
Summary
- Quadratic Equation in Standard Form: ax2+ bx + c = 0
- Quadratic Equations can be factored
- Quadratic Formula: x = −b ± √(b2 − 4ac) 2a
- When the Discriminant (b2−4ac) is: