How to calculate extrema?
The Steps
- Enter the function into the y = bank.
- Select the 2nd button, followed by the calc button.
- Select either maximum or minimum depending on the question.
- If the local extrema are not easily visible, adjust the window.
- The graph appears on the screen, with the words 'Left Bound?' Move the cursor to the left of the extrema, hit enter.
How to find extrema of a function?
- Verify the function is continuous on [a,b]. ...
- Find the derivative and determine all critical values of f f that are in (a,b). ...
- Evaluate the function at the critical values found in Step 2 and the endpoints x= a x = a and x = b x = b of the interval.
157 Course Notes/sec_Extrema.html More items...
How to calculate local extrema?
- Take a number line and put down the critical numbers you have found: 0, –2, and 2. ...
- Pick a value from each region, plug it into the first derivative, and note whether your result is positive or negative. ...
- Take your number line, mark each region with the appropriate positive or negative sign, and indicate where the function is increasing and decreasing. ...
How to find absolute maximum value?
Here are the steps to keep in mind when finding the function’s absolute maximum:
- Make sure that the function is continuous within the interval.
- Find the critical numbers of the function within the interval. Recall that we can find the critical numbers of $f (x)$ by equating $\boldsymbol {f^ {\prime} (x)}$ to zero.
- Evaluate $f (x)$ at the critical numbers and the endpoints. ...

How do you find the absolute extrema?
Finding the Absolute ExtremaFind all critical numbers of f within the interval [a, b]. ... Plug in each critical number from step 1 into the function f(x).Plug in the endpoints, a and b, into the function f(x).The largest value is the absolute maximum, and the smallest value is the absolute minimum.
What's the difference between relative and absolute extrema?
So, relative extrema will refer to the relative minimums and maximums while absolute extrema refer to the absolute minimums and maximums.
What is an example of absolute maximum?
Since f(3/4) > 0 this means x = 3/4 is an absolute maximum of the function f(x). So x = 0 is the only critical value of f(x).
What's the difference between local and absolute extrema?
All local extrema are points at which the derivative is zero (though it is possible for the derivative to be zero and for the point not to be a local extrema). While they can still be endpoints (depending upon the interval in question), the absolute extrema may be determined with a few shortcuts, too.
How do you determine if a graph has an absolute extrema?
0:2017:16Finding Absolute Maximum and Minimum Values - Absolute ExtremaYouTubeStart of suggested clipEnd of suggested clipAnd this point is a relative or a local minimum. Now to identify the location of the absoluteMoreAnd this point is a relative or a local minimum. Now to identify the location of the absolute extrema you simply have to compare the Y values.
How do you find the extrema of a function?
Finding Absolute Extrema of f(x) on [a,b]Verify that the function is continuous on the interval [a,b] .Find all critical points of f(x) that are in the interval [a,b] . ... Evaluate the function at the critical points found in step 1 and the end points.Identify the absolute extrema.
What is the difference between absolute maxima and minima?
An absolute maximum point is a point where the function obtains its greatest possible value. Similarly, an absolute minimum point is a point where the function obtains its least possible value.
How do you find local and absolute extrema on a graph?
0:599:44Absolute and Local Extrema - YouTubeYouTubeStart of suggested clipEnd of suggested clipTerm. This point down here is called a local minimum a local minimum so we're with the graph changesMoreTerm. This point down here is called a local minimum a local minimum so we're with the graph changes from decreasing to increasing.
What defines a relative extrema?
Relative extrema are simply the bumps and dips on a function's graph. These are located by tracking where the function changes from increasing to decreasing (relative maximum) or decreasing to increasing (relative minimum).
Is an absolute max also a relative Max?
Yes. Yes, not every local max is an absolute max, but every absolute max is a local max (same with min). All an absolute max/min is, is just a local max/min that is greater/lesser than every other local max/min.
What is the difference between relative maximum and local maximum?
Here are the definitions, a relative maximum and is sometimes called the local maximum, f has a relative maximum at x=c if of c is the largest value of f near c, and relative minimum f has a relative minimum at x=c if f of c is the smallest value of f near c.
What counts as relative extrema?
Graphically, relative extrema are the peaks and valleys of the graph of a function, peaks being the points of relative maxima and valleys being the points of relative minima. The combination of relative maxima and minima is called the relative extrema.
What is an extrema?
Extrema are the maximum or minimum values of a function, and there are two types of extrema we will be focusing on:
Where can absolute extremes be found?
It’s important to point out that Absolute Extrema can occur within the interval or at the endpoints. In contrast, Local Extrema can only be found within the open interval and never at an endpoint.
What is the extreme value theorem?
The Extreme Value Theorem states that if f is a continuous function on a closed interval [a,b], then f will have an absolute minimum f (c) and an absolute maximum f (d) at some values c and d in the interval.
What is the critical number of a function?
The theorem states that a critical number of a function f is a number c in the domain such that f’ (c) = 0 or f’ is undefined.
Can we substitute critical number and endpoints into absolute extrema?
Now we substitute the critical number and both endpoints into the function to determine absolute extrema.
What is the absolute extremum of a function?
An absolute extremum (or global extremum) of a function in a given interval is the point at which a maximum or minimum value of the function is obtained. Frequently, the interval given is the function's domain, and the absolute extremum is the point corresponding to the maximum or minimum value of the entire function.
Why are extrema important in calculus?
Extrema (maximum and minimum values) are important because they provide a lot of information about a function and aid in answering questions of optimality. Calculus provides a variety of tools to help quickly determine the location and nature of extrema.
What is an extremum in math?
contributed. An extremum (or extreme value) of a function is a point at which a maximum or minimum value of the function is obtained in some interval. A local extremum (or relative extremum) of a function is the point at which a maximum or minimum value of the function in some open interval containing the point is obtained.
When to find local extrema?
Many local extrema may be found when identifying the absolute maximum or minimum of a function.
What is the maximum of a function?
In simpler terms, a point is a maximum of a function if the function increases before and decreases after it. Conversely, a point is a minimum if the function decreases before and increases after it.
Is a point a minimum?
In simpler terms, a point is a maximum of a function if the function is concave down, and a point is a minimum of a function if the function is concave up. The derivative tests may be applied to local extrema as well, given a sufficiently small interval.
Is there an absolute minimum or maximum?
There may not exist an absolute maximum or minimum if the region is unbounded in either the positive or negative direction or if the function is not continuous. If the function is not continuous (but is bounded), there will still exist a supremum or infimum, but there may not necessarily exist absolute extrema. If the function is continuous and bounded and the interval is closed, then there must exist an absolute maximum and an absolute minimum.
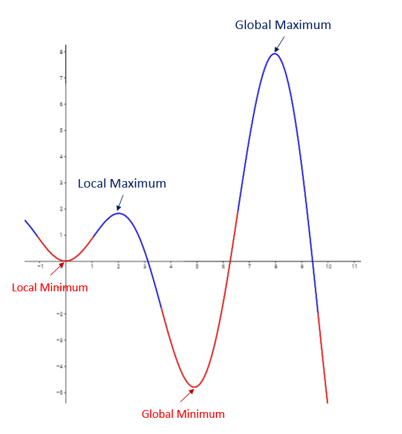
Figure 1
The largest y -value on the graph is the absolute maximum, and the smallest y -value on the graph is the absolute minimum.
Definition: Absolute Extrema
Suppose f is a function on the interval [a, b]. Then, ∙ The y -value f(c) is an absolute maximum if f(c) ≥ f(x) on [a, b] . ∙ The y -value f(c) is an absolute minimum if f(c) ≤ f(x) on [a, b] .
Example 2
In addition, f ′ (x) is not defined at x = 0 but neither is the original function, so it is not a critical value.
What is the difference between absolute extrema and relative extrema?
The absolute extrema will refer to the absolute minimums and maximums, while the relative extrema will refer to the relative minimums and maximums. Note that relative extrema do not occur at the endpoints of a domain. Unlike the absolute extrema, they only occur interior to the domain.
Where does absolute maximum occur?
An absolute maximum occurs at the x value where the function is the biggest . In contrast, a local maximum occurs at an x value if the function is more prominent than points around it (i.e., an open interval around it).
What is the difference between absolute minimum and local minimum?
A local minimum occurs at an x value if the function is smaller than the points around it. In contrast, an absolute minimum occurs at the x value where the function is the smallest (i.e., an open interval around it).
What is the absolute maximum value?
Definitions. Intuitively, the absolute maximum value is the largest of the possible values of , and similarly for minimum. Notice that a function may reach its maximum (or minimum) at more than one -value.
When a function is defined on a closed interval, an absolute extreme value may occur at the endpoint of that?
Notice that when a function is defined on a closed interval, an absolute extreme value may occur at the endpoint of that interval of domain, since the endpoint of the interval may yield the largest value of f on that closed interval.
What is the max/min value?
Graphically, this means that the max/min value is the maximum/minimum height of the graph at some x = c . Then x = c is where the max/min occurs.
What is relative extrema?
Relative (local) extrema: These are the turning points in the domain of function at which function has a value which is greater (for maxima) or smaller (for minima) then the values at its neighbouring points. There can be more than one relative maxima or minima for a function.
What is the absolute maxima?
Absolute extrema: These extreme values are found on a closed interval. Absolute maxima is the greatest value of the continuous function for given closed interval and absolute minima is the smallest value of continuous function on given closed interval. It may be at critical points or at the end points of given closed interval. There can be only one abs. maximum or minimum value for given domain.
Is an airport in the capital city an absolute extrema?
All these state airports are local (relative) extrema. But There is an international airport in the capital city which serves international flights connecting to other countries. This international airport is absolute extrema. There can be more than one one local maxima and minima (like many state airports) but there is only one absolute maxima and minima like international airport in capital city.
What is the absolute minimum?
An absolute minimum is the lowest point of a function/curve on a specified interval. Collectively maxima and minima are known as extrema. 🔗.
What is the difference between relative maximum and relative minimum?
🔗#N#A relative maximum is a location on a curve where all points near it are lower. A relative minimum is a location on a curve where all points near it are higher.
What is the value of c in the domain of a function?
A value c in the domain of a function f is a relative minimum of f if and only if there exists some interval ( a, b) in the domain containing c such that f ( c) ≤ f ( x) for all . x ∈ ( a, b).
What are Relative Extrema?
Relative extrema are the input values of a function f (x) where f (x) has minimum or maximum values. They can be of two types - relative maxima and relative minima. Graphically, relative extrema are the peaks and valleys of the graph of a function, peaks being the points of relative maxima and valleys being the points of relative minima.
Relative Extrema Definition
The relative extrema of a function are points on the graph of a function at which the minimum or maximum values of the function are obtained in some interval of the domain of the function. Let us go through the definitions of relative maxima and relative individually:
Finding Relative Extrema
We can evaluate the relative extrema of a function using derivative tests. There are two tests, namely:
Relative Extrema First Derivative Test
Now, to find the relative extrema using the first derivative test, we check the change in the sign of the first derivative of the function as we move through the critical points. The slope of the graph of the function is given by the first derivative.
Relative Extrema Second Derivative Test
Next, to find the points of relative extrema using the second derivative test, we check the sign of the second derivative of the function at the critical points. Generally, if the first derivative test fails, then we use the second derivative test to find the points of relative extrema.
Relative Extrema Examples
Example 1: Determine the points of relative extrema of the function f (x) = 2 - x 2
FAQs on Relative Extrema
Relative extrema are the input values of a function f (x) where f (x) has minimum or maximum values. They can be of two types - relative maxima and relative minima.
What is the absolute extremum of a function?from brilliant.org
An absolute extremum (or global extremum) of a function in a given interval is the point at which a maximum or minimum value of the function is obtained. Frequently, the interval given is the function's domain, and the absolute extremum is the point corresponding to the maximum or minimum value of the entire function.
Why are extrema important in calculus?from brilliant.org
Extrema (maximum and minimum values) are important because they provide a lot of information about a function and aid in answering questions of optimality. Calculus provides a variety of tools to help quickly determine the location and nature of extrema.
What is an extremum in math?from brilliant.org
contributed. An extremum (or extreme value) of a function is a point at which a maximum or minimum value of the function is obtained in some interval. A local extremum (or relative extremum) of a function is the point at which a maximum or minimum value of the function in some open interval containing the point is obtained.
When to find local extrema?from brilliant.org
Many local extrema may be found when identifying the absolute maximum or minimum of a function.
What is the maximum of a function?from brilliant.org
In simpler terms, a point is a maximum of a function if the function increases before and decreases after it. Conversely, a point is a minimum if the function decreases before and increases after it.
Is there an absolute minimum or maximum?from brilliant.org
There may not exist an absolute maximum or minimum if the region is unbounded in either the positive or negative direction or if the function is not continuous. If the function is not continuous (but is bounded), there will still exist a supremum or infimum, but there may not necessarily exist absolute extrema. If the function is continuous and bounded and the interval is closed, then there must exist an absolute maximum and an absolute minimum.
Is Extrema easy to maintain?from extremausa.com
We keep it simple. Every Extrema machine is designed to be easy to maintain, be simple to repair, and use many “off the shelf” components.