
How do you identify difference of two squares?
a^2 - b^2 equals (a+b) (a-b) In mathematics, the difference of two squares is a squared (multiplied by itself) number subtracted from another squared number. Every difference of squares may be factored according to the identity. a 2 − b 2 = ( a + b ) ( a − b ) {displaystyle a^ {2}-b^ {2}= (a+b) (a-b)}
How do you use the difference of two squares?
Difference of Two Squares Formula. The trick to factorising the difference of two squares is to use the formula, textcolor{blue}{a^2 -b^2 = (a+b)(a-b)} This can be used in either direction to factorise or expand such expressions quickly. To show that this works, we will expand the two brackets of the general formula.
How do you factor the difference of two squares?
To factor using the difference of squares, we can follow the following steps:
- Extract the common factor if there is one. Don’t forget to include this common factor in your final answer.
- Determine the numbers that will produce the same results and use the formula .
- Factor and simplify the resulting expression if possible.
What two numbers squared equal a perfect square?
The following are the properties of the square numbers:
- A number with 2, 3, 7 or 8 at unit’s place should never be a perfect square. ...
- If the number of zeros at the end is even, then the number is a perfect square number. ...
- If the even numbers are squared, it always gives even numbers. ...
- If the natural numbers other than one is squared, it should be either a multiple of 3 or exceeds a multiple of 3 by 1.

How do you find difference of two squares?
1:113:22Factoring the Difference of Two Squares - Ex 1 - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe want something we want to rewrite the first term is something squared well to write 9 asMoreWe want something we want to rewrite the first term is something squared well to write 9 as something squared we would need a 3 and then to get x squared we just need an X.
What is the result of difference of two squares?
The Difference of Two Squares theorem tells us that if our quadratic equation may be written as a difference between two squares, then it may be factored into two binomials, one a sum of the square roots and the other a difference of the square roots. This is sometimes shown by the expression A² - B² = (A + B) (A - B).
How do you do the difference of squares step by step?
To factor a difference of squares, the following steps are undertaken: Check if the terms have the greatest common factor (GCF) and factor it out. Remember to include the GCF in your final answer. Determine the numbers that will produce the same results and apply the formula: a2– b2 = (a + b) (a – b) or (a – b) (a + b)
Which shows a difference of squares?
Solution: The difference of two squares is a theorem that tells us if a quadratic equation can be written as a product of two binomials, in which one shows the difference of the square roots and the other shows the sum of the square roots.
What is the form of difference of squares identity?
Identity. The difference of two squares identity is ( a + b ) ( a − b ) = a 2 − b 2 (a+b)(a-b)=a^2-b^2 (a+b)(a−b)=a2−b2.
What is the product of two square numbers?
Product of two square numbers is always a square number.
What is the difference of two squares?
The difference of two squares is a theorem that tells us if a quadratic equation can be written as a product of two binomials, in which one shows the difference of the square roots and the other shows the sum of the square roots. One thing to note about this theorem is that it does not apply to the SUM of squares.
How to Factor Difference of Squares?
In this section, we will learn how to factorize algebraic expressions using the difference of square formula . To factor a difference of squares, the following steps are undertaken:
What is the difference between a and c in math?
The term ‘a’ is referred to as the leading coefficient, while ‘c’ is the absolute term of f (x). Every quadratic equation has two values of the unknown variable, usually known as the roots of the equation (α, β).
Summary of the difference of squares
Remember that the difference of squares is a theorem that tells us whether a quadratic equation can be written as the product of two binomials. One of these binomials shows the difference of the square roots and the other binomial shows the sum of the square roots. A difference of squares is expressed in the form:
Difference of squares – Examples with answers
The following difference of squares examples follow the steps detailed above to obtain the factorization of the algebraic expressions. Try to solve the exercises yourself before looking at the solution.
Difference of squares – Practice problems
Solve the following difference of squares problems to test your knowledge on this topic. The solved examples above can be used to review the solving process if you have problems.
See also
Interested in learning more about algebraic expressions? Take a look at these pages:
Why do we have a difference of two squares?
Clearly, we have a difference of two squares because the sign between the two squared terms is subtraction. For this example, the solution is broken down in just a few steps to highlight the procedure. Once you get comfortable with the process, you can skip a lot of steps.
When you have a binomial with each term being squared (having an exponent of 2 ),?
Whenever you have a binomial with each term being squared (having an exponent of 2 ), and they have subtraction as the middle sign, you are guaranteed to have the case of difference of two squares.
Why is an exponent of a variable always a perfect square?
Why? Because all even numbers are factorable by the number 2.
How to combine like terms?
You may keep it in that form as your final answer. But the best answer is to combine like terms by adding or subtracting the constants. This also simplifies the answer by getting rid of the inner parenthesis.
Can you factor out a difference of two squares?
After verifying that you have a difference of two squares, you can now factor it out as a product of two binomials with alternating signs in the middle, positive and negative.
Is the second parenthesis a case of difference of two squares?
Are we done? Nope! The second parenthesis is still a case of difference of two squares. We have no choice but to factor it out one more time.
Is the first term of a binomial a perfect square?
The first term of the binomial is definitely a perfect square because the variable. x. x x is being raised to the second power. However, the second term of the binomial is not written as a square. So we need to rewrite it in such a way that. 9. 9 9 is expressed as some number with a power of. 2. 2 2.
What is the difference between two squares?
In mathematics, the difference of two squares is a squared (multiplied by itself) number subtracted from another squared number. Every difference of squares may be factored according to the identity
Which ancient civilization used the difference of two squares to calculate multiplication?
Historically, the Babylonians used the difference of two squares to calculate multiplications.
Is the proof that a and b have equal norms?
The proof is identical. For the special case that a and b have equal norms (which means that their dot squares are equal), this demonstrates analytically the fact that two diagonals of a rhombus are perpendicular. This follows from the left side of the equation being equal to zero, requiring the right side to equal zero as well, and so the vector sum of a + b (the long diagonal of the rhombus) dotted with the vector difference a - b (the short diagonal of the rhombus) must equal zero, which indicates the diagonals are perpendicular.
Can you use complex conjugates in reverse?
Since the two factors found by this method are complex conjugates, we can use this in reverse as a method of multiplying a complex number to get a real number. This is used to get real denominators in complex fractions.
Is the difference of two consecutive perfect squares odd?
Therefore, the difference of two consecutive perfect squares is an odd number . Similarly, the difference of two arbitrary perfect squares is calculated as follows:
What is the difference of two squares?
A difference of squares is a binomial of the form: a2 – b2. Take note that the first term and the last term are both perfect squares. When we factor a difference of two squares, we will get. a2 – b2 = ( a + b ) ( a – b) This is because ( a + b ) ( a – b) = a2 – ab + ab – b2 = a2 – b2. Example:
Why is it important to recognize patterns in a trinomial?
In some cases recognizing some common patterns in the trinomial or binomial will help you to factor it faster. For example, we could check whether the binomial is a difference of squares.
How to write a square root in a parenthesis?
1) Write two parent hesis. 2) Put a in one and a in the othe. 3) Take the square root of the first term and put that in the front of each parenthesis. 4) Take the square root of the last term and put that in the back of each parenthesis.
How to factor binomials?
1) It must be a binomial (have two terms) 2) Both terms must be perfect squares (meaning that you could take the square root and they would come out evenly.) 3) There must be a subtraction/negative sign (not addition) in between them. If these three requirements are met, then we can easily factor the binomial using the pattern.
Calculator Use
This is a factoring calculator if specifically for the factorization of the difference of two squares. If the input equation can be put in the form of a 2 - b 2 it will be factored. The work for the solution will be shown for factoring out any greatest common factors then calculating a difference of 2 squares using the idenity:
Difference of Two Squares when a is Negative
If both terms a and b are negative such that we have -a 2 - b 2 the equation is not in the form of a 2 - b 2 and cannot be rearranged into this form.
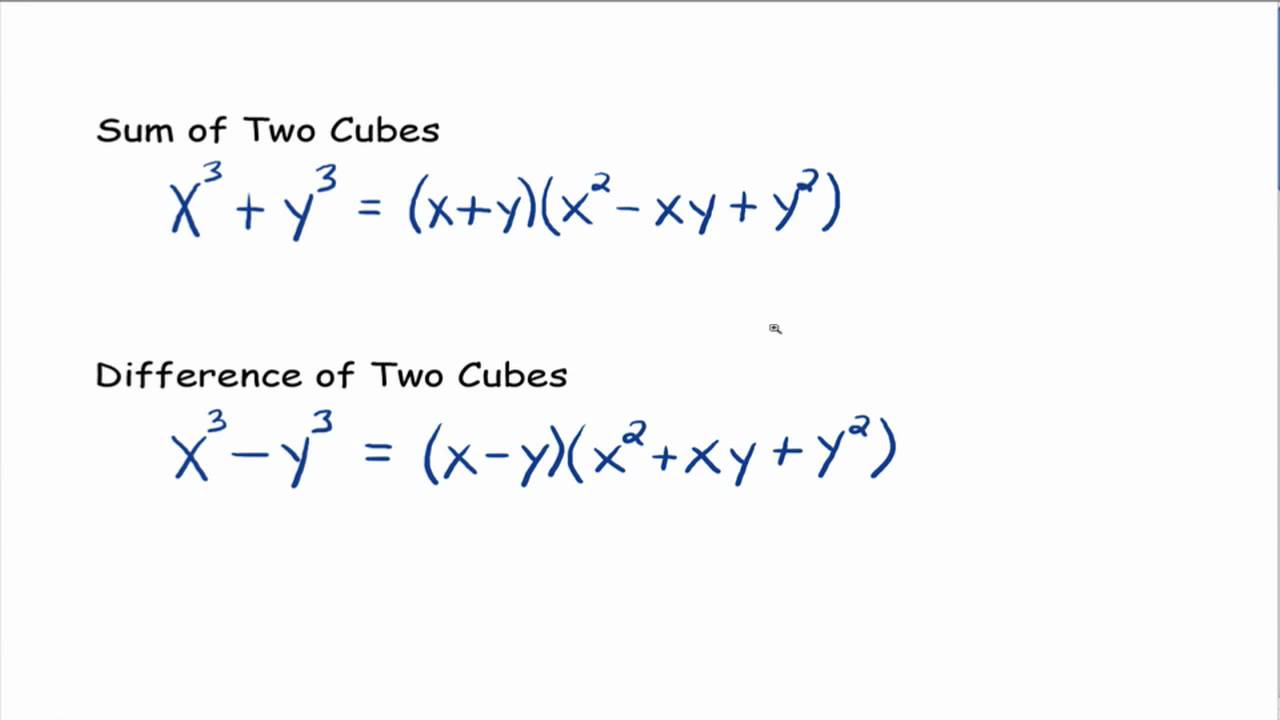
Summary of The Difference of Squares
Difference of Squares – Examples with Answers
- The following difference of squares examples follow the steps detailed above to obtain the factorization of the algebraic expressions. Try to solve the exercises yourself before looking at the solution. Start now: Explore our additional Mathematics resources
Difference of Squares – Practice Problems
- Solve the following difference of squares problems to test your knowledge on this topic. The solved examples above can be used to review the solving process if you have problems.
See Also
- Interested in learning more about algebraic expressions? Take a look at these pages: 1. Examples of Order of Operations 2. Examples of Simplifying Algebraic Expressions 3. Common Factor Exercises 4. Examples of the Distributive Property
Overview
In mathematics, the difference of two squares is a squared (multiplied by itself) number subtracted from another squared number. Every difference of squares may be factored according to the identity
in elementary algebra.
Uses
The formula for the difference of two squares can be used for factoring polynomials that contain the square of a first quantity minus the square of a second quantity. For example, the polynomial can be factored as follows:
As a second example, the first two terms of can be factored as , so we have:
Moreover, this formula can also be used for simplifying expressions:
Proof
The proof of the factorization identity is straightforward. Starting from the left-hand side, apply the distributive law to get
By the commutative law, the middle two terms cancel:
leaving
The resulting identity is one of the most commonly used in mathematics. Among many uses, it g…
Geometrical demonstrations
The difference of two squares can also be illustrated geometrically as the difference of two square areas in a plane. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e. . The area of the shaded part can be found by adding the areas of the two rectangles; , which can be factorized to . Therefore, .
Generalizations
The identity also holds in inner product spaces over the field of real numbers, such as for dot product of Euclidean vectors:
The proof is identical. For the special case that a and b have equal norms (which means that their dot squares are equal), this demonstrates analytically the fact that two diagonals of a rhombus are perpendicular. This follows from the left side of the equation being equal to zero, requiring the ri…
History
Historically, the Babylonians used the difference of two squares to calculate multiplications.
For example:
93 x 87 = 90² - 3² = 8091
64 x 56 = 60² - 4² = 3584
See also
• Congruum, the shared difference of three squares in arithmetic progression
• Conjugate (algebra)
• Factorization
Notes
1. ^ Complex or imaginary numbers TheMathPage.com, retrieved 22 December 2011
2. ^ Multiplying Radicals TheMathPage.com, retrieved 22 December 2011
3. ^ "Babylonian mathematics".