An overidentified model is a model for which there is more than enough information in the data to estimate the model parameters. By contrast, an underidentified model has insufficient information from the data to estimate the free parameters, and a just-identified model has just enough information to solve for the free parameters.
What is the difference between just-identified and over-identified models?
According to this pdf, when number of instrument variable equals to the number of endogenous components, the model is said to be just-identified; if number of instrument variable is bigger than the number of endogenous components, the model is said to be over-identified. I have these questions regarding this statement:
How to test if an equation or model is overidentified?
If an equation or model is overidentified, tests of overidentifying restrictions must be applied to check the validity of instruments. When an equation or model is just or exactly-identified, such tests are not applicable. To illustrate the procedure of the test, let us consider an overidentified simultaneous equation model.
Can an over identified model have more than one solution?
My intuition says that for an over identified model will have more than one solution and after iteration if the converged solution fits the data well then only we can conclude something about the model as compared to the scenario with just identified model where we always get a perfect fit. Am I thinking about it correctly ?
What is Overidentification of endogenous regressor?
If you have access to one of the instruments to instrument the endogenous regressor schooling, your model is just identified. If you have access to both, you have two IVs for just one endogenous regressor, so you have overidentification. Thanks for contributing an answer to Cross Validated!
What is the difference between an exactly identified and over identified model give an example?
If you have access to one of the instruments to instrument the endogenous regressor schooling, your model is just identified. If you have access to both, you have two IVs for just one endogenous regressor, so you have overidentification.
What is a just identified model in SEM?
An identified model in which the number of free parameters exactly equals the number of known values, i.e, a model with zero degrees of freedom. Note that not all models in which the knowns equal the unknown are identified and so these models are not identified. The example model is just-identified.
What is the difference between SEM and regression analysis?
There are two main differences between regression and structural equation modelling. The first is that SEM allows us to develop complex path models with direct and indirect effects. This allows us to more accurately model causal mechanisms we are interested in. The second key difference is to do with measurement.
Is SEM the same as path analysis?
Path Analysis is a causal modeling approach to exploring the correlations within a defined network. The method is also known as Structural Equation Modeling (SEM), Covariance Structural Equation Modeling (CSEM), Analysis of Covariance Structures, or Covariance Structure Analysis.
What is default model in Amos?
AMOS Research Model with results Notes for Model (Default model) Computation of degrees of freedom (Default model) Number of distinct sample moments: 464 Number of distinct parameters to be estimated: 91 Degrees of freedom (464 -91): 373 Result (Default model) Minimum was achieved Chi-square = 3301.887 Degrees of ...
Why is system identification important?
System identification requires that your data capture the important dynamics of your system. Good experimental design ensures that you measure the right variables with sufficient accuracy and duration to capture the dynamics you want to model.
How many parameters does SEM have?
In addition, the covariance between these residuals is estimated by default. So this adds up to 2 residual variances + 1 residual covariance for the Y1 & Y2 outcome variables + the 5 regression paths, which brings our total number of freely estimated parameters to 8.
What is identification econometrics?
Identification in econometrics is usually taken to be the problem of relating the structural parameters of a simulta- neous-equation model to the reduced-form parameters that "summarize all relevant information available from the sam- ple data" (Intriligator 1978, p. 342).
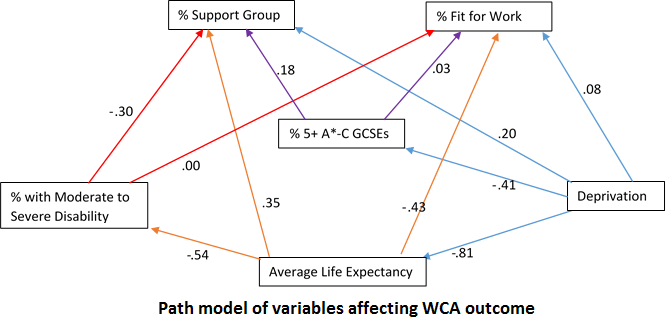
Specification of the Model
To illustrate the procedure of the test, let us consider an overidentified simultaneous equation model. We will use the same model that we estimated in Two-Stage Least Squares (2SLS) Estimation.
Application and interpretation in practice
The test results can be easily computed using statistical software packages. We do not need to carry out the test manually.
