what is angular momentum proportional to

Full Answer

Is angular momentum proportional to inertia?

angular momentum L is proportional to moment of inertia I and angular speed ω measured in radians per second. Unlike mass, which depends only on amount of matter, moment of inertia is also dependent on the position of the axis of rotation and the shape of the matter.

Is angular momentum proportional to radius?

Angular momentum is directly proportional to square root of radius.

What does angular momentum depend on?

Angular momentum depends on the rotational velocity of an object, but also its rotational inertia. When an object changes its shape (rotational inertia), its angular velocity will also change if there is no external torque.

What is angular momentum analogous to?

Angular momentum is completely analogous to linear momentum. It has the same implications in terms of carrying rotation forward, and it is conserved when the net external torque is zero.

Does angular momentum increase or decrease with radius?

Angular momentum is defined as L=r×p where r is the center of rotation and p is the momentum. Since angular momentum is conserved, if r decreases then p must increase.

What happens to angular momentum if radius increases?

If you increase radius, you increase angular momentum, and thus decrease the precession frequency.

On what does the angular momentum of an object depend quizlet?

Angular momentum depends on mass, speed, and radius. Acceleration toward the center of a circular path. A force directed toward the center of a circle that keeps an object moving in a circular path.

Does mass affect angular momentum?

With other variables held constant, as mass increases, angular momentum increases. Thus, mass is directly proportional to angular momentum.

What is the relation between angular momentum and frequency?

There exists an important relationship between angular velocity and frequency and it is given by the following formula: angular velocity is equal to the product of the frequency and the constant 2pi. The constant 2pi comes from the fact that one revolution per second is equivalent to 2pi radians per second.

How does torque relate to angular momentum?

Torque is the rotational equivalent of force and Angular Momentum is the rotational equivalent of Translational Momentum. This can be extended to rotational motion as follows, →τ=d→Ldt . So Torque is the rate of change of Angular Momentum.

Is angular momentum completely analogous to linear momentum?

Making Connections. Angular momentum is completely analogous to linear momentum, first presented in Uniform Circular Motion and Gravitation. It has the same implications in terms of carrying rotation forward, and it is conserved when the net external torque is zero.

Is angular momentum equal to linear momentum?

The magnitude of the angular momentum of an orbiting object is equal to its linear momentum (product of its mass m and linear velocity v) times the perpendicular distance r from the centre of rotation to a line drawn in the direction of its instantaneous motion and passing through the object's centre of gravity, or ...

Does angular momentum decrease as radius decreases?

In the case of a satellite orbiting around a planet, the angular momentum is also dependent on the radius of the orbit. For example, at a given speed, the angular momentum of a satellite will increase as the radius of the orbit increases. So, something moving in a larger orbit will have more angular momentum.

Does increasing radius increase angular velocity?

Angular speed does not change with radius Angular speed ω does not change with radius, but linear speed v does. For example, in a marching band line going around a corner, the person on the outside has to take the largest steps to keep in line with everyone else.

What is r in angular momentum?

Angular Momentum Formula r is the radius (distance between the object and the fixed point about which it revolves)

What is angular momentum in simple words?

angular momentum, property characterizing the rotary inertia of an object or system of objects in motion about an axis that may or may not pass through the object or system.

Calculate the angular momentum of a pulley of 2 kg, radius 0.1 m, rotating at a constant angular velocity of 4 rad/sec

Substitute the given values like m=2 kg and r=0.1 m in I=(1/2)mr² (formula of the moment of inertia) we get I= 0.01 kg.m 2 Angular momentum is giv...

Give the expression for Angular momentum.

\(\begin{array}{l}\vec{L}=\vec{I} \times \vec{\omega }\end{array} \) or \(\begin{array}{l}\vec{L}=\vec{r} \times \vec{p}\end{array} \)

For an isolated rotating body, how are angular velocity and radius related?

For an isolated rotating body, angular velocity is inversely proportional to the radius.

Write the dimensional formula for Angular momentum.

The dimensional formula is ML 2 T -1

When an ice-skater goes for a spin, what happens to her spinning speed when she stretches her hands?

Spinning speed reduces.

How can an ice-skater increase his/her spinning speed?

By bringing hands closer, thus reducing the radius increases the angular velocity.

If the moment of inertia of an isolated system is halved. What happens to its angular velocity?

Angular velocity will be doubled.

Calculate the angular moment of the object. When an object with the moment of inertia I = 5 kg.m² is made to rotate 1 rad/sec speed.

Substituting the given value in formula L=Iω we get L=5 kg.m 2 .s -1 .

1. What is the importance of angular momentum?

Angular momentum is an extremely important topic as it finds great relevance in the study of celestial objects. Almost all objects in the universe,...

2. What is the right-hand thumb rule?

The right-hand thumb rule or Flemings Right-Hand thumb rule is a very widely used principle used in physics to find the cross-product of vector qua...

3. What is torque?

Torque is a physical quantity that is used in physics and mechanics. In terms of Mechanics, it is also considered as the equivalent of Linear force...

4. What is the relation between spin and torque?

We can say that for a continuous rigid object, the total angular momentum is equal to the volume integral of angular momentum density over the enti...

5. What is a radian?

Radian is the SI unit for the calculation of the angular displacement. While calculating the length traveled by a rotating body, what we are actual...

What is angular momentum?

Angular momentum, in physics, is a property that characterizes the rotatory inertia of an object in motion about the axis that may or may not pass through the specified object. The Earth’s rotation and revolution are the best real-life examples of angular momentum. For instance, the annual revolution that the Earth carries out about ...

Which rule gives the direction of angular momentum?

The right-hand thumb rule gives the direction of angular momentum and states that if someone positions his/her hand in a way that the fingers come in the direction of r, then the fingers on that hand curl towards the direction of rotation, and thumb points towards the direction of angular momentum (L), angular velocity, and torque.

What happens to velocity if no torque is applied?

Hence, if no torque is applied, then the perpendicular velocity of the object will alter according to the radius (the distance between the centre of the circle, and the centre of the mass of the body). It means velocity will be high for a shorter radius and low for a longer one. Share this with your friends. Share.

What does the formula L mean in physics?

Note: The equation or formula L = r⊥mv representing the angular momentum of an object changes only when you apply a net torque. Hence, if no torque is applied, then the perpendicular velocity of the object will alter according to the radius (the distance between the centre of the circle, and the centre of the mass of the body). It means velocity will be high for a shorter radius and low for a longer one.

How is torque related to angular momentum?

Here, torque is defined as the rate of change of angular momentum. Torque is related to angular momentum in a way similar to how force is related to linear momentum. Now, when we know what the angular momentum and torque are, let's see how these two are related. To see this, we need to find out how objects in rotational motion get moving or spinning in the first position. Let's take the example of a wind turbine. We all know that it's the wind that makes the turbine spins. But how is it doing so? Well, the wind is pushing the turbine's blade by applying force to blades at some angles and radius from the axis of rotation of the turbine. In simple words, the wind is applying torque to the turbine. Hence, it is torque what gets rotatable objects spinning when they are standing still. Moreover, if the torque is applied to an object which is already spinning in the same direction in which it is spinning, it upsurges its angular velocity. Hence, we can say that torque is directly proportional to the angular velocity of a rotating body. Since torque can change the angular velocity, it can also change the amount of angular momentum as the angular momentum depends on the product of the moment of inertia and angular velocity. This is how torque is related to angular momentum.

What is the torque applied to a turbine?

In simple words, the wind is applying torque to the turbine. Hence, it is torque what gets rotatable objects spinning when they are standing still. Moreover, if the torque is applied to an object which is already spinning in the same direction in which it is spinning, it upsurges its angular velocity.

Which rule is used to determine the direction of the angular momentum vector?

The direction of the angular momentum vector, in this case, is the same as the axis of rotation of the given object and is designated by the right-hand thumb rule.

Why do particles have more angular momentum?

If you had two spheres of the same mass---like a large wooden ball and a small lead ball---then, at the same rate of rotation, the larger one would have more angular momentum! That's because of two reasons. Particles further away from the axis contribute more to the angular momentum at a given speed. But they also move faster just because they are further away from the axis. So overall, the amount a particle contributes to the angular momentum is proportional to the square of its distance from the axis.

Why does momentum stay the same?

That's because momentum is conserved. A moving object has momentum, so it has to keep moving at the same velocity in order for its momentum to stay the same. The only way for the object to stop moving is for it to transfer its momentum to another object. (That's what force is: it's the transfer of momentum.)

What happens to momentum when momentum is conserved?

If momentum is conserved it means that given a fixed mass, then velocity does not change. Now imagine such a mass is being pulled normal to its velocity such that it is now rotating in a circle. If the radius of that circle is small, the mass will rotate faster than if the radius was large.

What is the torque of an object?

Torque if u know is T=Fd or force times distance from the axis of rotation. For any rotating object, they create circles when they rotate. From the middle of any circle to the outside is the radius. So if a force is applied to the outside of an object perpendicular to the distance from the axis of rotation it will rotate and keep going if theres no friction.

What happens when you set a rigid body in rotation?

In the same way, when you set a rigid body in rotation, it will tend to continue rotating at the same speed, around the same axis---unless acted on by a torque. We say that rotating bodies have angular momentum. Angular momentum is conserved, and the only way for an object to stop rotating is if its angular momentum is transferred to another object. (That's what torque is: the transfer of angular momentum.)

How to tell if an object has momentum?

But when the object moves through an axis, or parallel to the axis, it does not have angular momentum around that axis. You have to flick the edge of the coin, so that your finger does not pass through the coin's diameter. That way your finger will have angular momentum around the coin's diameter, and the coin will rotate about its own diameter as the axis. If you flick the centre of the coin, the coin will still move, as linear momentum would be transferred from your finger. However, the coin will not spin, as your finger will not have any angular momentum to transfer to it.

Why does the mass traveling in a larger circle have to travel a longer distance?

Now, looking at it the other way, if the time it takes to complete one revolution remains constant, then the mass rotating around the larger circle has to have a velocity with a higher magnitude than the mass rotating in a smaller circle. This is because the mass traveling in a larger circle has to travel a longer distance.

What is angular momentum?

e. In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational equivalent of linear momentum. It is an important quantity in physics because it is a conserved quantity —the total angular momentum of a closed system remains constant.

Who discovered angular momentum?

Leonhard Euler, Daniel Bernoulli, and Patrick d'Arcy all understood angular momentum in terms of conservation of areal velocity, a result of their analysis of Kepler's second law of planetary motion. It is unlikely that they realized the implications for ordinary rotating matter.

What is an example of decreasing moment of inertia?

As an example, consider decreasing of the moment of inertia, e.g. when a figure skater is pulling in her/his hands, speeding up the circular motion. In terms of angular momentum conservation, we have, for angular momentum L, moment of inertia I and angular velocity ω :

What is the second moment of mass?

is the particle's moment of inertia, sometimes called the second moment of mass. It is a measure of rotational inertia. Moment of inertia (shown here), and therefore angular momentum, is different for every possible configuration of mass and axis of rotation.

How does a figure skater decrease her moment of inertia?

A figure skater in a spin uses conservation of angular momentum – decreasing her moment of inertia by drawing in her arms and legs increases her rotational speed.

What is conservation of momentum?

The conservation of angular momentum helps explain many observed phenomena, for example the increase in rotational speed of a spinning figure skater as the skater's arms are contracted, the high rotational rates of neutron stars, the Coriolis effect, and the precession of gyroscopes.

What is the sum of all internal torques of a system?

The net external torque on any system is always equal to the total torque on the system; in other words, the sum of all internal torques of any system is always 0 (this is the rotational analogue of Newton's Third Law ).

How to Calculate Orbital Angular Momentum?

We can calculate the orbital angular momentum by using the following orbitals taken as an example:

Who explained the angular momentum of an electron?

Later on, Louis de Broglie explained the postulate of the quantization of the angular momentum of an electron given by Bohr. He stated that an electron in motion shows the behavior of a particle-wave.

What is linear momentum?

Ans: Linear momentum is the product of mass and velocity, whereas the angular momentum is the product of mass and angular velocity. The unit is measured in kilogram meter square.

Which postulate is successfully proven by de Broglie hypothesis?

So, we can infer that Bohr’s second postulate is successfully proven by de Broglie hypothesis.

Does an electron have momentum?

Ans: Yes, the electron does possess angular momentum. The angular momentum of an electron can be found as per the relation given by Bohr.

Is angular momentum a conserved quantity?

Ans: Yes , the angular momentum is a conserved quantity, as it is a major quantity. According to the physicists, the angular momentum is the rotational equivalent of the linear momentum. Therefore, in a closed-loop/structure, the total angular momentum is said to be constant. Q4.

Can particle waves drive towards standing waves?

Under the resonant conditions, particle waves can drive towards the standing waves. If we pull out a stationary string plucked, the excitement of wavelength occurs. As per the findings, it is inferred that the waves that have nodes can survive the angular momentum, and later on, they create standing waves in the string.

How are angular momentum and momentum different?

Well, angular momentum and momentum both are different by their different functionality. Electrons are always revolving around the nucleus. It possesses angular momentum. So, the angular momentum of an electron is the rotation or the spinning of the electron around the nucleus. [Image will be Uploaded Soon]

Why does angular momentum promote spin?

This is generated due to the collision of momentum-based electrons with the wall. The angular momentum promotes the spin of electrons after the collision.

What is the angular momentum of an electron in a D orbital?

The angular momentum of the electron in d orbital is equal to √6 (h/2π). We obtain the result with the help of the formula √l (l+1) h/2π. Here, l = 2 as it is d-orbital.

What is orbital momentum?

Introduction to Orbital Angular Momentum. Momentum explains the multiplication of velocity and mass can give rise to the momentum of a body. When a body is in motion with a certain amount of mass, it possesses momentum. Well, angular momentum and momentum both are different by their different functionality. Electrons are always revolving ...

Which postulate has proven the second postulate of Bohr?

In the above process, de Broglie’s hypothesis has proven the second postulate of Bohr successfully. The hypothesis from de Broglie has made its start from the quantization of angular momentum of the revolving electron. Students can gain another conclusion about the quantized electron orbits and energy states. Both of them are present because of the wave nature of the electron.

Which statement is not good enough to postulate the reason for the angular momentum and orbiting of electrons around?

He made a statement that electrons can travel to the selected orbits only where an electron’s angular momentum is an integral product of h/2. Bohr's statement was not good enough to postulate the reason for the angular momentum and orbiting of electrons around the nucleus.

Which atomic model has specific comments on the angular momentum of electrons?

Those arrangements of electrons can vary as they are in different orbits around the nucleus. Bohr’s atomic model has some specific comments on the angular momentum of electron s. Bohr suggested that the electrons that are revolving around the nucleus are quantized.

What is momentum in motion?

Momentum is the measure of an object's movement with respect to its mass and velocity. So it is determined as the product of mass and velocity. An object moving in linear motion, will experience linear momentum.

Is momentum angular or circular?

Similarly, if an object moves in circular motion, then the momentum will be angular momentum. So it is measured as the product of moment of inertia with angular velocity.

What is the angular momentum of a particle?

The numerical value of angular momentum of a particle is the product of a specific radius multiplied by the momentum; however it is not usually the radius (r) between the origin and the particle itself. The relevant radius is the shortest distance (h) between the origin and the line along which the particle is travelling instantaneously. This is the same as the radius to the particle times the sine of the angle (theta) between the radius and the direction of motion. Of course, angular momentum is a vector, and its direction is perpendicular to the plane

What is the equation for angular momentum?

L = p x r where L is the angular momentum, p the linear momentum, and r the radius between the origin and the particle. L, p and r represent vectors when empoldened, and x represents the cross product.

What is the angular momentum of a mass on a string of length?

Interestingly it does not depend on whether the momentum is from circular or linear motion. If a mass on a string of length is orbiting a point with momentum p, its angular momentum is pr. But if the string breaks then the mass flies off along the tangent to the circle at the point where the string broke, and its angular momentum remains pr where r is the length of the perpendicular dropped from O (the original center of rotation) to the tangent, i.e. the distance of O from the trajectory (not from the mass).

What does it mean when an object rotates around a fulcrum?

If you’re talking about an object like a ball on a string or a planet, then the fact that it is rotating around a fulcrum means there is a force applied onto it, which means that the linear momentum is changing as it rotates, at least in direction. If the orbit is elliptical, then the linear momentum is also changing in magnitude as the object accelerates and decelerates - though angular momentum is unchanged.

What is proportional to the square of a linear dimension?

For an object of given mass and shape, I is proportional to the square of linear dimensions. This means that I is proportional to radius squared for an object for which has a radius.

Is linear momentum conserved?

You can understand this by assuming an ant hitting a truck, in this case also linear momentum ( not only of ant ,but of ant-truck system) is conserved, though truck's position remains undisturbed.

Is the Sun's position fixed?

Similarily, it goes for sun planet system. In our solar system Sun's position is asssumed fixed, and planet revolves maintaining the angular momentum to be conserved.

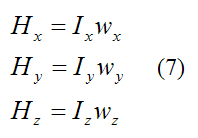
Overview

Definition in classical mechanics

Analogy to linear momentum

Conservation of angular momentum

Angular momentum in orbital mechanics

Solid bodies

Angular momentum in general relativity

Angular momentum in quantum mechanics