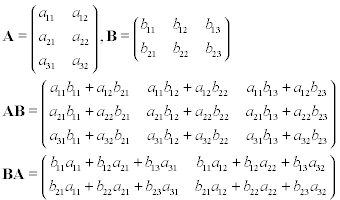The three basic elementary operations or transformation of a matrix are:
- Interchange of any two rows or two columns.
- Multiplication of row or column by a non-zero number.
- Multiplication of row or column by a non-zero number and add the result to the other row or column.
Why is elementary transformation of matrices important?
Elementary transformation of matrices is very important. It is used to find equivalent matrices and also to find the inverse of a matrix. Elementary transformation is playing with the rows and columns of a matrix.
What is elementary transformation in maths?
It is used to find equivalent matrices and also to find the inverse of a matrix. Elementary transformation is playing with the rows and columns of a matrix. Let us learn how to perform the transformation on matrices. As the name suggests, only the rows of the matrices are transformed and NO changes are made in the columns.
What is elementary row transformation in matrix?
Elementary Row Transformation: As the name suggests, only the rows of the matrices is transformed and NO changes are made in the columns. These row operations are executed according to certain set of rules which make sure that the transformed matrix is equivalent to the original matrix.
What are the elementary operations of matrices?
In order to transform a matrix into a specific required form, some operations are done, known as elementary operations or transformation of matrices. There are six operations (transformations) on a matrix, three of which are due to rows and three due to columns, which are known as elementary operations or transformations.

What is an elementary matrix example?
The matrix M is called a left-inverse of A because when it is multiplied to the left of A, we get the identity matrix....Introducing the left inverse of a square matrix.MatrixElementary row operationElementary matrix[102−1010−1001−1]R1←R1+(−2)R3M4=[10−2010001][1001010−1001−1]3 more rows
How many types of elementary transformations are there?
three kindsThere are three kinds of elementary row transformations.
How do you solve an elementary transformation matrix?
0:001:39Elementary Transformation Of Matrices - YouTubeYouTubeStart of suggested clipEnd of suggested clipNumber one is interchanging of course that is if you interchange the rows of the original matrix andMoreNumber one is interchanging of course that is if you interchange the rows of the original matrix and get a new matrix. There won't be any change in the solution operation.
What is elementary method?
Elementary methods consist of arithmetic, geometry, and high school algebra. These are the only tools that may be used in the branch of number theory known as elementary number theory.
What are the 3 elementary row operations?
The three elementary row operations are: (Row Swap) Exchange any two rows. (Scalar Multiplication) Multiply any row by a constant. (Row Sum) Add a multiple of one row to another row.
How do you identify an elementary matrix?
1:024:54Elementary Matrices - YouTubeYouTubeStart of suggested clipEnd of suggested clipLet's look at some examples to determine if this given matrix is an elementary matrix we want toMoreLet's look at some examples to determine if this given matrix is an elementary matrix we want to determine if we can perform one row operation on the identity matrix to transform it into this matrix.
Which of the following is elementary transformation?
Elementary transformations can either be of rows (elementary row operations) or of columns (elementary column operations) but we cannot operate both simultaneously.
Can an elementary transformation change the rank of a matrix?
By applying the elementary transformation to a matrix, its rank does not change. Elementary transformations are those operations performed on rows and columns of the matrices to transform them into a different form.
How do you find the inverse of a matrix using elementary transformation?
Thus, in general if we want to evaluate the inverse of matrix A, by using elementary row operations on A = IA, in a sequence, until we get: I = BA. Also, by using elementary column operations, on A = AI, in a sequence, till we get I = AB, we can get the value of the inverse of matrix A.
What does elementary mean in maths?
In mathematics, an elementary function is a function of a single variable (typically real or complex) that is defined as taking sums, products, and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, and exponential functions, including possibly their inverse functions (e.g., arcsin, log, or ...
Can we use column transformation in elementary transformation?
So, yes we can use column operations in elementary transformation.
What is an elementary row replacement matrix?
Answer and Explanation: The only way an elementary row replacement matrix can be formed is by replacing a specific row with the sum between the row and a multiple of a different row within the matrix. This is not the same as multiplying the row by a constant value or interchanging rows with another row in the matrix.
What are the 7 transformations in math?
These are Transformations:RotationTurn!ReflectionFlip!TranslationSlide!
How many types of transformations are there?
4 typesTranslation, reflection, rotation, and dilation are the 4 types of transformations.
What are the 4 transformations in maths?
There are 4 types of transformation: translation, rotation, reflection, and enlargement.
What are the different types of transformations?
There are four main types of transformations: translation, rotation, reflection and dilation.
1. How is the Rank of a Matrix Determined using Elementary Transformations?
The number of linearly independent row vectors or linearly independent column vectors in a matrix is called the rank of a matrix. By applying row t...
2. Explain Briefly, the Matrix Notation.
Matrices are represented by uppercase bold English fonts. The order of the matrix is denoted as m x n where’ is the number of rows and ‘n’ is the n...
3. Explain the matrix notation.
Elements of matrices are noted in uppercase bold English fonts. The order of matrices is represented through rows and columns which is written in t...
4. What is the elementary transformation of a matrix?
A matrix is mainly a rectangular arrangement of various symbols, numbers that represent a set of data in any system. The elements of matrices are a...
What is Elementary Transformation of Matrices?
Elementary Transformation of Matrices means playing with the rows and columns of a matrix. Or operations are done on the rows and columns of matric...
In the operation of a row, the entire row in a matrix is swapped with another row?
Yes, in the operation of a row, the entire row in a matrix is swapped with another row.
Can we multiplied row or column with the same non zero number?
Yes, the entire row or column is multiplied with the same non zero number.
Can we use column operations in elementary transformation?
Elementary transformation of matrices is very important. It is used to find equivalent matrices and also to find the inverse of a matrix. So, yes...
What is transformed matrix?
These row operations are executed according to a certain set of rules which make sure that the transformed matrix is equivalent to the original matrix. These rules are:
Why is elementary transformation important?
Elementary transformation of matrices is very important. It is used to find equivalent matrices and also to find the inverse of a matrix. Elementary transformation is playing with the rows and columns of a matrix. Let us learn how to perform the transformation on matrices.
When are two matrices equal?
We have already seen that two matrices are equal when they are of the same order and their corresponding elements are equal . That is, if = and = are two matrices such that = , then: For every value of i and j, = . But there is another way to compare matrices. In this case, the matrices are equivalent to each other.
Does the change reflect in the ith row?
An important thing to note here is that the change will only reflect in the elements of ith i t h row. The elements of jth j t h row will remain same.
What is elementary transformation?
Elementary transformations are operations done on the rows and columns of matrices to change their shape so that the computations become easier . It is also used to discover the inverse of a matrix, the determinants of a matrix, and to solve a system of linear equations.
Why is fundamental transformation important?
Playing with the rows and columns of a matrix is an example of elementary transformation. Elementary row (or column) operations on polynomial matrices are essential because they allow polynomial matrices to be patterned into simpler forms, such as triangular and diagonal forms.
What is the difference between the left and right multiplication matrix?
A matrix that differs from the identity matrix by one elementary row operation is called an elementary matrix. The left multiplication (pre-multiplication) of an elementary matrix represents primary row operations, whereas the right multiplication (post-multiplication) represents elementary column operations.
How to determine a matrix's rank?
We determine a matrix's rank by the number of linearly independent columns it contains (or rows). A null matrix has no non-zero rows or columns. As a result, no separate rows or columns exist. As a result, a null matrix has a rank of zero.
Is a square matrix an elementary matrix?
A square matrix is always an elementary matrix. Remember the row operations defined in. Any elementary matrix, denoted by E, is produced by performing the one-row operation on the identity matrix of the same size.
Can you do elementary transformations in two columns at the same time?
Elementary transformations can be of rows (elementary row operations) or columns (elementary column operations), but not both at the same time.
Do simple row operations reduce the matrix?
A sequence of elementary row operations may reduce any matrix to a uniquely reduced Echelon form. Simple row operations do not affect the solution set of any linear system. As a result, the solution set of a system is the same as the solution set of a system whose augmented matrix is in reduced echelon form.
What Is Transformation Matrix?
Transformation matrix is a matrix that transforms one vector into another vector. The positional vector of a point is changed to another positional vector of a new point, with the help of a transformation matrix.
Types of Transformation Matrix
The transformation matrix transforms a vector into another vector, which can be understood geometrically in a two-dimensional or a three-dimensional space. The frequently used transformations are stretching, squeezing, rotation, reflection, and orthogonal projection. Let us learn about some of these transformations in detail.
Application of Transformation Matrix
The transformation matrix has numerous applications in vectors, linear algebra, matrix operations. The following are some of the important applications of the transformation matrix.
Examples on Transformation Matrix
Example 1: Find the new vector formed for the vector 5i + 4j, with the help of the transformation matrix [2 −3 1 2] [ 2 − 3 1 2].
FAQs on Transformation Matrix
Transformation Matrix is used to transform one vector into another vector by the process of matrix multiplication. The position vector of a point is represented as a column matrix, and the number of elements in this column matrix is equal to the components of the vector.