what is fibonacci heap in data structure

Full Answer

What is Fibonacci heap?

Like Binomial Heap, Fibonacci Heap is a collection of trees with min-heap or max-heap property. In Fibonacci Heap, trees can have any shape even all trees can be single nodes (This is unlike Binomial Heap where every tree has to be Binomial Tree).

Which pointer is maintained at the minimum element node in Fibonacci heap?

A pointer is maintained at the minimum element node. It consists of a set of marked nodes. (Decrease key operation) The trees within a Fibonacci heap are unordered but rooted. The roots of all the trees are linked together for faster access.

How do you merge two heaps in Fibonacci sequence?

In Fibonacci heaps, merging is accomplished by simply concatenating two lists containing the tree roots. Compare the roots of the two heaps to be merged, and whichever is smaller becomes the root of the new combined heap. The other tree is added as a subtree to this root. This can be done in constant time.

What are the Fibonacci numbers?

The Fibonacci numbers are the terms of a sequence of integers in which each term is the sum of the two previous terms with F1 = F2 = 1, Fn = Fn−1 +Fn−2. ◻ 1. Like binomial heaps, Fibonacci heaps use doubly linked lists to allow for O(1) time for operations such as splicing off a part of a list, merging two lists,...

What is Fibonacci heap used for?

Fibonacci heaps are used to implement the priority queue element in Dijkstra's algorithm, giving the algorithm a very efficient running time. Fibonacci heaps have a faster amortized running time than other heap types. Fibonacci heaps are similar to binomial heaps but Fibonacci heaps have a less rigid structure.

Why is it called Fibonacci heap?

The fibonacci heap is called a fibonacci heap because the trees are constructed in a way such that a tree of order n has at least Fn+2 nodes in it, where Fn+2 is the (n + 2)th Fibonacci number.

How do you create a Fibonacci heap?

Insertion: To insert a node in a Fibonacci heap H, the following algorithm is followed:Create a new node 'x'.Check whether heap H is empty or not.If H is empty then: Make x as the only node in the root list. Set H(min) pointer to x.Else: Insert x into root list and update H(min).

What are the two types of heap?

Generally, Heaps can be of two types:Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it's children. ... Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it's children.

Is Fibonacci heap used in practice?

To the best of my knowledge, there are no major applications that actually use Fibonacci heaps or Brodal queues. Fibonacci heaps were initially designed to satisfy a theoretical rather than a practical need: to speed up Dijkstra's shortest paths algorithm asymptotically.

What are three main properties of heap?

Properties of HeapOrdering. Nodes must be arranged in an order according to values. The values should follow min-heap or max-heap property. ... Structural. All levels in a heap should be full. ... Methods or Operations of Heap. find - in order to find an item in a heap. ... Implementation. Heaps are usually implemented in an array.

What are the two properties of heap?

Thus we may say that a heap satisfies two properties: A "shape property" (that is, it's a complete binary tree) An "order property" (the value in a node is "optimal" with respect to the values in all nodes below it)

What is heap with example?

A heap is a tree-based data structure in which all the nodes of the tree are in a specific order. For example, if is the parent node of , then the value of follows a specific order with respect to the value of and the same order will be followed across the tree.

What is the algorithm for Fibonacci?

How to Generate Fibonacci Series? The Fibonacci numbers upto certain term can be represented as: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….. or 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…. Eighth Term = Sixth + Seventh = 5+8 = 13 … and so on to infinity!

Why memory is called heap?

It is called heap because it is a pile of memory space available to programmers to allocate and de-allocate. Every time when we made an object it always creates in Heap-space and the referencing information to these objects are always stored in Stack-memory.

How many types heap?

two typesThere are two types of the heap: Min Heap. Max heap.

What is difference between heap and stack?

Key Differences The Heap Space contains all objects are created, but Stack contains any reference to those objects. Objects stored in the Heap can be accessed throughout the application. Primitive local variables are only accessed the Stack Memory blocks that contain their methods.

Why is it called a heap data structure?

It is called heap because it is a pile of memory space available to programmers to allocate and de-allocate. Every time when we made an object it always creates in Heap-space and the referencing information to these objects are always stored in Stack-memory.

Who invented Fibonacci heap?

Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis. For the Fibonacci heap, the find-minimum operation takes constant (O(1)) amortized time.

How Fibonacci heap is different from binomial heap?

In Fibonacci Heap, trees can have any shape even all trees can be single nodes (This is unlike Binomial Heap where every tree has to be a Binomial Tree). Fibonacci Heap maintains a pointer to a minimum value (which is the root of a tree).

What is called heap?

: a collection of things thrown one on another : pile. : a great number or large quantity : lot. heap.

Why is Fibonacci heap called Fibonacci heap?

Fibonacci heap are mainly called so because Fibonacci numbers are used in the running time analysis. Also, every node in Fibonacci Heap has degree at most O (log n) and the size of a subtree rooted in a node of degree k is at least F k+2, where F k is the kth Fibonacci number.

What is heap used for?

Heaps are mainly used for implementing priority queue. We have discussed below heaps in previous posts.

Which heap beats the binary heap?

In terms of Time Complexity, Fibonacci Heap beats both Binary and Binomial Heaps.

What is the reduced time complexity of decrease key?

The reduced time complexity of Decrease-Key has importance in Dijkstra and Prim algorithms. With Binary Heap, time complexity of these algorithms is O (VLogV + ELogV). If Fibonacci Heap is used, then time complexity is improved to O (VLogV + E)

What is the potential of a Fibonacci heap?

Therefore, the potential of the heap is 9 (3 trees + 2 × (3 marked-vertices)). A Fibonacci heap is a collection of trees satisfying the minimum-heap property, that is, the key of a child is always greater than or equal to the key of the parent. This implies that the minimum key is always at the root of one of the trees.

Why use Fibonacci heaps?

Using Fibonacci heaps for priority queues improves the asymptotic running time of important algorithms, such as Dijkstra's algorithm for computing the shortest path between two nodes in a graph, compared to the same algorithm using other slower priority queue data structures.

Why are Fibonacci heaps so slow?

Fibonacci heaps have a reputation for being slow in practice due to large memory consumption per node and high constant factors on all operations. Recent experimental results suggest that Fibonacci heaps are more efficient in practice than most of its later derivatives, including quake heaps, violation heaps, strict Fibonacci heaps, rank pairing heaps, but less efficient than either pairing heaps or array-based heaps.

What are the drawbacks of Fibonacci heaps?

Although Fibonacci heaps look very efficient, they have the following two drawbacks: 1 They are complicated when it comes to implementing them. 2 They are not as efficient in practice when compared with the theoretically less efficient forms of heaps. In their simplest version they require storage and manipulation of four pointers per node, whereas only two or three pointers per node are needed in other structures, such as Binary heap, Binomial heap, Pairing heap, Brodal queue and Rank pairing heap.

How many units of time are stored in a heap?

Thus, the root of each tree in a heap has one unit of time stored. This unit of time can be used later to link this tree with another tree at amortized time 0. Also, each marked node has two units of time stored. One can be used to cut the node from its parent. If this happens, the node becomes a root and the second unit of time will remain stored in it as in any other root.

How many pointers per node in a binary heap?

In their simplest version they require storage and manipulation of four pointers per node, whereas only two or three pointers per node are needed in other structures, such as Binary heap, Binomial heap, Pairing heap, Brodal queue and Rank pairing heap.

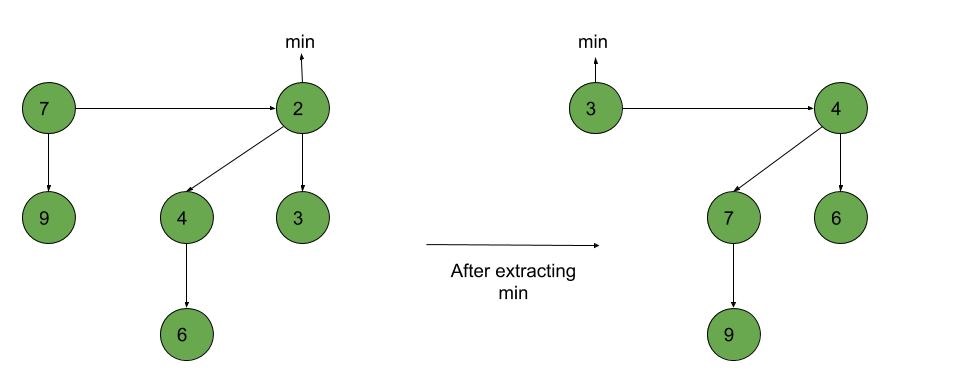
How does extract minimum work?

Operation extract minimum (same as delete minimum) operates in three phases. First we take the root containing the minimum element and remove it. Its children will become roots of new trees. If the number of children was d, it takes time O ( d) to process all new roots and the potential increases by d −1. Therefore, the amortized running time of this phase is O ( d) = O (log n ).

What is a fibonacci heap?

A fibonacci heap is a data structure that consists of a collection of trees which follow min heap or max heap property. We have already discussed min heap and max heap property in the Heap Data Structure article. These two properties are the characteristics of the trees present on a fibonacci heap.

Why is Fibonacci heap called Fibonacci Heap?

The fibonacci heap is called a fibonacci heap because the trees are constructed in a way such that a tree of order n has at least F n+2 nodes in it, where F n+2 is the (n + 2) th Fibonacci number. Fibonacci Heap.

What are the characteristics of trees present on a fibonacci heap?

In a fibonacci heap, a node can have more than two children or no children at all. Also, it has more efficient heap operations than that supported by the binomial and binary hea ps. The fibonacci heap is called a fibonacci heap because ...

What to do if heap is empty?

If the heap is empty, set the new node as a root node and mark it min.

What is the potential of a Fibonacci heap?

It has three trees of degrees 0, 1, and 3. Three vertices are marked (shown in blue). Therefore, the potential of the heap is 9 (3 trees + 2 × (3 marked-vertices) [2]

Why use Fibonacci heaps?

Fibonacci heaps are used to implement the priority queue element in Dijkstra’s algorithm, giving the algorithm a very efficient running time. Fibonacci heaps have a faster amortized running time than other heap types. Fibonacci heaps are similar to binomial heaps but Fibonacci heaps have a less rigid structure.

How does Fibonacci work?

The children of each node are also related using a linked list. For each node, the linked list maintains the number of children a node has and whether the node is marked. The linked list also maintains a pointer to the root containing the minimum key. A node is marked to indicate if any of its children were removed. This is important so the heap can keep track of how far removed its shape is becoming from a binomial heap. If a Fibonacci heap is too different from a binomial heap, it loses many of the efficient time operations that their binomial nature gives it.

What happens when binomial heaps are consolidated?

Binomial heaps, on the other hand, consolidate immediately. Consolidation occurs when heap properties are violated, for example, if two heaps have the same order, the heaps must be adjusted to prevent this. Deleting the minimum element is done in three steps.

What is the minimum element of a Fibonacci heap?

Fibonacci heaps must satisfy the min-heap property (or max-heap property if making a max-heap) where every node’s children must have a smaller value than it (the parent), and therefore, the minimum element will always be at the root of one of the trees.

What is insert in fibonacci?

Insert. Insertion to a Fibonacci heap is similar to the insert operation of a binomial heap. A heap of one element is created and the two heaps are merged with the merge function. The minimum element pointer is updated if necessary. The total number of nodes in the tree increases by one.

Do binomial and fibonacci heaps merge?

Binomial heaps merge heaps immediately but Fibonacci heaps wait to merge until the extract-min function is called. While Fibonacci heaps have very good theoretical complexities, in practice, other heap types such as pairing heaps are faster.

Fibonacci Heap Introduction

A Fibonacci heap is a heap data structure like a binomial heap. It uses Fibonacci numbers and furthermore used to execute the priority queue element in Dijkstra’s most limited way algorithm which reduces the time complexity from O (m log n) to O (m + n log n), giving the algorithm an enormous boost in terms running time.

Properties of a Fibonacci Heap

It is a set of min heap-ordered trees. (for example, The parent is consistently smaller than the children.)

Memory Representation of the Nodes in a Fibonacci Heap

The roots of all the trees are connected together for quicker access. The child nodes of a parent node are associated with each other through a circular doubly linked list as demonstrated beneath.

What is a fibonacci heap?

In computer science, a Fibonacci heap is a heap data structure consisting of a forest of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987. The name of Fibonacci heap comes from Fibonacci numbers which are used in the running time analysis.

What is the difference between t and m in Fibonacci?

where t is the number of trees in the Fibonacci heap, and m is the number of marked nodes. A node is marked if at least one of its children was cut since this node was made a child of another node (all roots are unmarked).

How does extract minimum work?

Operation extract minimum (same as delete minimum) operates in three phases. First we take the root containing the minimum element and remove it. Its children will become roots of new trees. If the number of children was d, it takes time O ( d) to process all new roots and the potential increases by d -1. Therefore the amortized running time of this phase is O ( d) = O (log n ).

How many units of time are stored in a heap?

Thus, the root of each tree in a heap has one unit of time stored. This unit of time can be used later to link this tree with another tree at amortized time 0. Also, each marked node has two units of time stored. One can be used to cut the node from its parent. If this happens, the node becomes a root and the second unit of time will remain stored in it as in any other root.

Which is better, Fibonacci or Binomial?

A Fibonacci heap is thus better than a binomial heap when b is asymptotically smaller than a. Using Fibonacci heaps for priority queues improves the asymptotic running time of important algorithms, such as Dijkstra's algorithm for computing shortest paths in a graph, and Prim's algorithm for computing a minimum spanning tree of a graph.

How to decrease the number of roots in the second phase?

In the second phase we therefore decrease the number of roots by successively linking together roots of the same degree. When two roots u and v have the same degree, we make one of them a child of the other so that the one with smaller key remains the root. Its degree will increase by one. This is repeated until every root has a different degree. To find trees of the same degree efficiently we use an array of length O (log n) in which we keep a pointer to one root of each degree.

Is Fibonacci heaps real time?

For this reason Fibonacci heaps and other amortized data structures may not be appropriate for real-time systems.

Motivation: Why Fibonacci Heaps?

Before jumping into Fibonacci heaps, it's probably good to explore why we even need them in the first place. There are plenty of other types of heaps ( binary heaps and binomial heaps, for example), so why do we need another one?

Step One: Lazy Binomial Heaps

To start off building the Fibonacci heap, we're going to begin with a binomial heap and modify it try to make insertions take time O (1). It's not all that unreasonable to try this out - after all, if we're going to do a lot of insertions and not as many dequeues, it makes sense to optimize insertions.

Step Two: Implementing Decrease-Key

Right now, we have a "lazy binomial heap" rather than a Fibonacci heap. The real change between a binomial heap and a Fibonacci heap is how we implement decrease-key.

Step Three: Linked Lists Abound!

There is one final detail we have to talk about. The data structure I've described so far is tricky, but it doesn't seem catastrophically complicated. Fibonacci heaps have a reputation for being fearsome... why is that?

Conclusion

I hope this answer sheds some light on the mystery that is the Fibonacci heap. I hope that you can see the logical progression from a simpler structure (the binomial heap) to a more complex structure by a series of simple steps based on reasonable insights.

Overview

In computer science, a Fibonacci heap is a data structure for priority queue operations, consisting of a collection of heap-ordered trees. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time an…

Structure

Implementation of operations

Proof of degree bounds

Worst case

Practical considerations

External links