11 Examples of Geometry In Everyday Life
- Nature. The most important example of geometry in everyday life is formed by the nature surrounding humans. ...
- Technology. The most common example of geometry in everyday life is technology. ...
- Homes. ...
- Architecture. ...
- Art. ...
- Sports. ...
- Designing. ...
- Computer Aided Design- CAD. ...
- Mapping. ...
- Medicine. ...
What are some real life examples of geometry?
For example:
- A triangle is a 3 sided shape, and the measure of its 3 interior angles is 180˚
- A square, rectangle or quadrilateral are 4 sided shapes, and the measure of their interior angles is 360˚
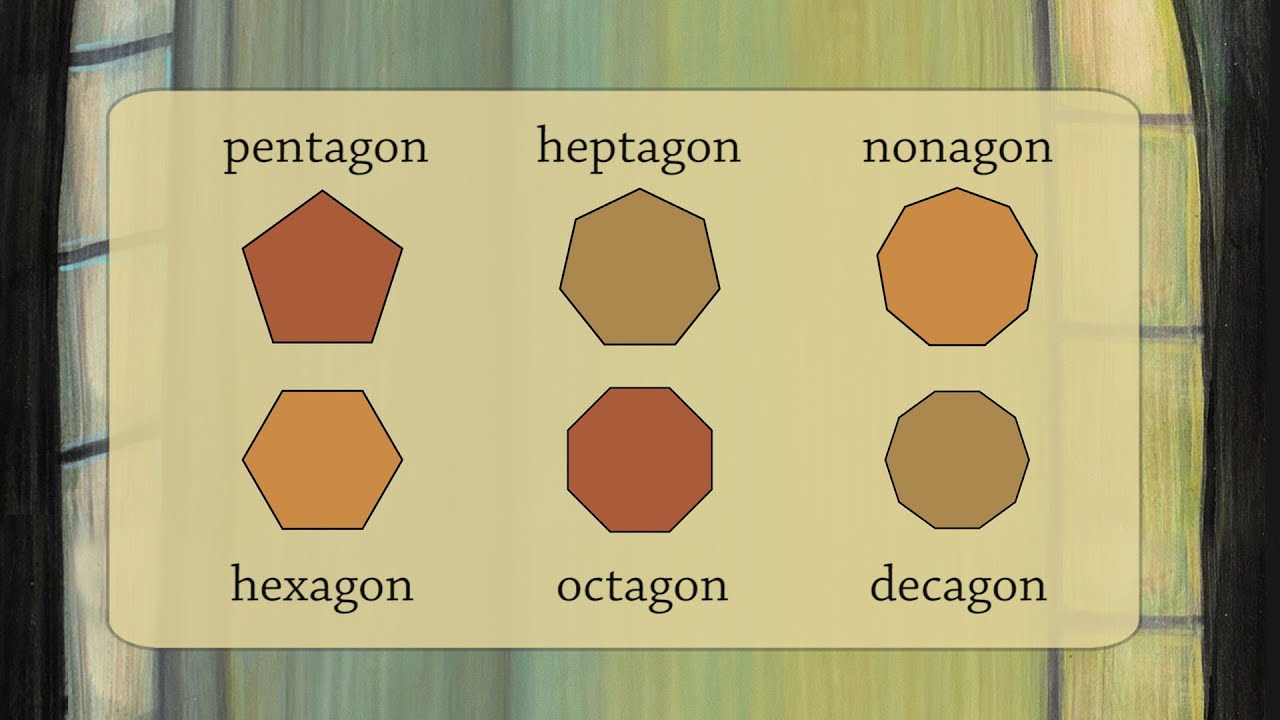
- Other polygons like the pentagon, hexagon, heptagon, octagon have 5, 6, 7, 8 sides respectively and varying angles.
Where to find examples of geometry in real life?
Examples of triangles in real life are:
- slices of pizza
- a sandwich cut diagonally
- some tortilla chips
- sails on a boat
- yield traffic signs
What are the three basic types of geometry?
- Hyperbolic
- Euclidian
- Ellipitic
What are some examples of geometry words?
Solution:
- Assign variables: Let x = size of one of the two equal angles Sketch the figure
- Write down the sum of angles in quadrilateral. The sum of angles in a quadrilateral is 360°
- Plug in the values from the question and from the sketch.
What is geometry explain?
Geometry is defined as “a branch of mathematics that deals with the measurement, properties, and relationships of points, lines, angles, surfaces, and solids.” Put even more simply, geometry is a type of math that deals with points, lines, shapes, and surfaces.
What are examples of geometry in real life?
The windows, doors, beds, chairs, tables, TV, mats, rugs, cushions, etc have different shapes. Moreover, bedsheets, quilts, covers, mats, and carpets have different geometric patterns on them. Geometry is also important cooking.
How many types of geometry are?
The three types of geometry are Euclidean, Hyperbolic, and Elliptical Geometry.
What are the basics of geometry?
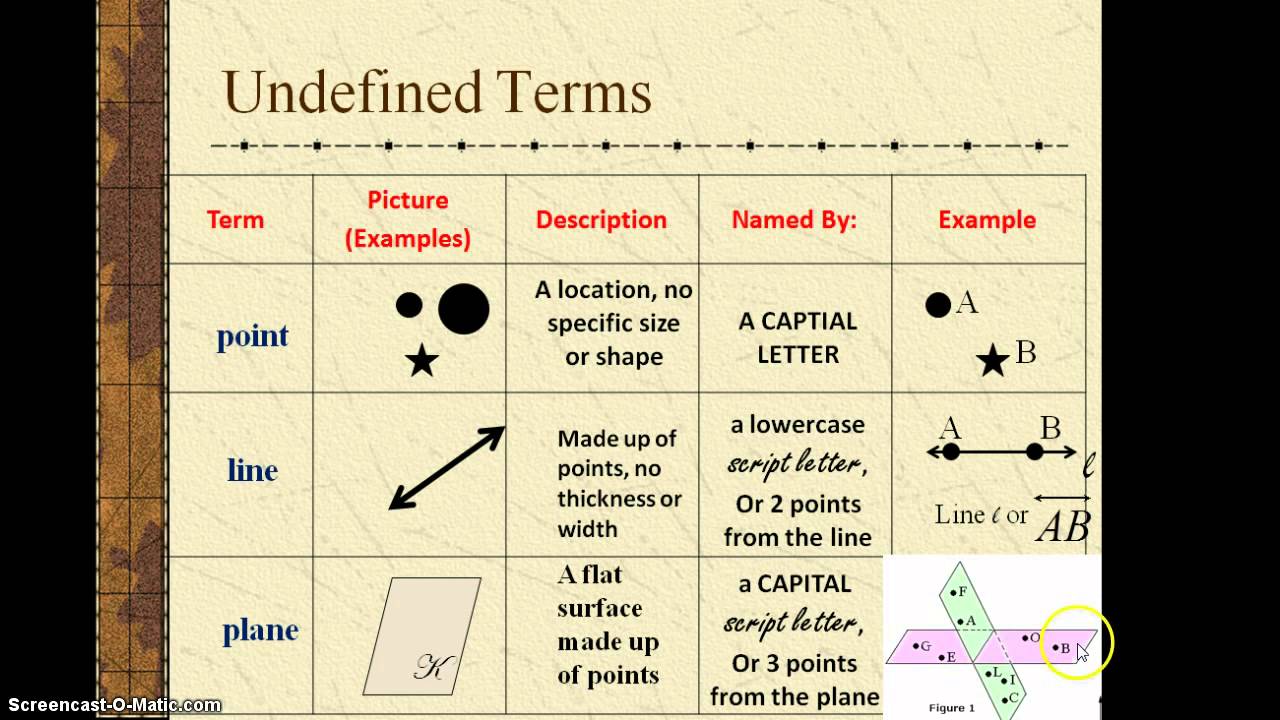
Answer: The basic geometrical concepts are dependent on three basic concepts. They are the point, line and plane. We cannot precisely define the terms. But, it refers to the mark of the position and has an accurate location.
How can you apply geometry in your life?
Geometry is used in various daily life applications such as art, architecture, engineering, robotics, astronomy, sculptures, space, nature, sports, machines, cars, and much more. Some of such applications used in daily life are mentioned below: Nature: One of the best examples of geometry in daily life is nature.
How important is geometry in our daily life?
Geometry helps us in deciding what materials to use, what design to make and also plays a vital role in the construction process itself. Different houses and buildings are built in different geometric shapes to give a new look as well as to provide proper ventilation inside the house.
What is geometry shape?
Geometric shapes are mathematical shapes. They are perfect and regular. They are characterised by straight lines, angles and points. An exception to this would be a perfect circle as it has no straight lines or points. Other geometric shapes are squares, rectangles, triangles, parallelograms, hexagons etc.
What is the most used geometry?
Euclidean Geometry Euclidean, or classical, geometry is the most commonly known geometry, and is the geometry taught most often in schools, especially at the lower levels. Euclid described this form of geometry in detail in "Elements," which is considered one of the cornerstones of mathematics.
How many branches are in geometry?
There are three major branches of geometry: Euclidean geometry, non-Euclidean geometry, and projective geometry. Euclidean geometry is the most common type of geometry and is the one that is taught in high school.
How do you teach geometry?
How to make Geometry InterestingUse Exciting Ways to Teach. ... Strengthen the Students' Understanding of the Principles of Geometry. ... Enhance the Problem Solving Skills of the Students. ... Understanding is the First Priority. ... Include Motivating Topics. ... Explore Geometry Dynamically. ... Use Effective Tools to Assess the Students.More items...
What is the formula of geometry?
Geometry formulas are used for finding dimensions, perimeter, area, surface area, volume, etc....List of Geometry Formulas.SHAPESFORMULAS2. TrianglePerimeter, P = a + b + c Area, A = ½ bh Height, h = 2(A/b) Where, a,b,c are the sides of a triangle.12 more rows
What is the symbol in geometry?
Table of symbols in geometry:SymbolSymbol NameMeaning / definition∥parallelparallel lines≅congruent toequivalence of geometric shapes and size~similaritysame shapes, not same sizeΔtriangletriangle shape19 more rows
What are some examples of plane geometry?
It does not deal with the depth of the shapes. Some examples of plane figures are square, triangle, rectangle, circle, and so on.
What is algebraic geometry?
(i) Algebraic Geometry – is a branch of geometry studying zeros of the multivariate polynomial. It includes linear and polynomial algebraic equations that are used for solving the sets of zeros. The application of this type comprises Cryptography, string theory, etc.
What is the point where the edges of a solid figure meet?
Vertices. A vertex is defined as the point where the edges of the solid figure meet at each other. In other words, it can be said that, the point where the adjacent sides of the polygon meet. The vertex is the corners where the edges meet. The number of vertices for different solid shapes in geometry is as follows:
What is the branch of mathematics that deals with shapes, angles, dimensions and sizes of a variety of things we see
Geometry is the branch of mathematics that deals with shapes, angles, dimensions and sizes of a variety of things we see in everyday life. In Euclidean geometry , there are two-dimensional shapes and three-dimensional shapes.
What are flat shapes called?
In plane geometry, 2 shapes such as triangles, squares, rectangles, circles are also called flat shapes. In solid geometry, 3d shapes such as a cube, cuboid, cone, etc. are also called solids. The basic geometry is based on points, line and plane, explained in coordinate geometry. The different types of shapes in geometry helps us to understand ...
What is the endpoint of an angle?
Angles in Geometry. In planar geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
What is the difference between similarity and congruence?
Similarity and Congruency. Similarity – Two figures are said to be similar if they have the same shape or have an equal angle but do not have the same size. Congruence – Two figures are said to be Congruent if they have the same shape and size. Thus, they are totally equal.
What are the two types of geometry?
Two types of geometry are plane geometry and solid geometry. Plane geometry deals with two-dimensional shapes and planes (x-axis and y-axis), while solid geometry deals with three-dimensional objects and 3D planes. These are the two types of geometry.
What is coordinate geometry?
Coordinate Geometry is a branch of geometry where the position of any given point on a plane is defined with the help of an ordered pair of numbers, or coordinates. Coordinate Geometry is introduced in Grade 9. It is a fun and interesting concept of mathematics. In coordinate geometry, we use a graph and plot points along the x-axis and y-axis. Let's go ahead and understand the concepts of coordinate geometry which includes topics starting from the basics such as labeling points on a number line, labeling points in a plane, cartesian system, straight-line distance, the distance formula, internal division, external division, area of a triangle, area of a quadrilateral, collinearity, lines parallel to the axes, slope-intercept form of a line, point-slope form, two-point form, general equation of a line, the intersection of two lines, circles centered at the origin, circles with arbitrary centers, and general equations of a circle.
What are the 5 postulates of Euclidean geometry?
There are 5 basic postulates of Euclidean Geometry that define geometrical figures. A straight line segment is drawn from any given point to any other. A straight line is extended indefinitely in both directions. A circle is drawn with any given point as its center and any length as its radius.
What is the branch of mathematics that is concerned with the shapes and sizes of objects, their relative position, and the properties
Geometry. Geometry (from the Ancient Greek: geo- "earth", -metron "measurement") is a branch of mathematics, that is primarily concerned with the shapes and sizes of the objects, their relative position, and the properties of space. There are many postulates and theorems applied by the Greek mathematician Euclid, ...
What is Euclidean geometry?
Euclidean Geometry refers to the study of plane and solid figures on the basis of axioms (a statement or proposition) and theorems. The fundamental concepts of Euclidean geometry include Points and Lines, Euclid’s Axioms and Postulates, Geometrical Proof, and Euclid’s Fifth Postulate.
What is the study of a sphere called?
Spherical geometry is the study of plane geometry on a sphere. Lines are defined as the shortest distance between the two points that lie along with them. This line on a sphere is an arc and is called the great circle. The sum of the angles in the triangle is greater than 180º.
What is the branch of mathematics that relates the principles covering distances, angles, patterns, areas, and volumes?
Geometry is the branch of mathematics that relates the principles covering distances, angles, patterns, areas, and volumes. All the visually and spatially related concepts are categorized under geometry. There are three types of geometry : Euclidean. Hyperbolic.
What is Geometry?
The branch of mathematics that deals with distances, angles, patterns, areas, and volumes is known as geometry. Geometry encompasses all the concepts visually and spatially related. It can be classified into three types:
Recommended Geometry Worksheets
Euclidean geometry is the study of geometry on a plane. Essentially, a plane is a two-dimensional surface that extends endlessly in both directions. Geometry and graph theory relies heavily on planes. The basic components that constitute planes in geometry are analogous to points, lines, and angles.
Angles in Geometry
Angles are formed when two straight lines or rays intersect at a point. Angles are typically measured in degrees. Angles can be acute, obtuse, right angled, straight angled, or obtuse. Angle pairs can be supplementary or complementary. It is an intricate component of geometry to construct angles and lines.
Plane Shapes in Geometry
We can identify and classify plane shapes based on their properties. Geometric shapes of the plane are flat shapes or two-dimensional shapes. A polygon is a closed curve with more than two lines. Triangles are closed figures with three sides and three vertices. Triangles have many theorems arising from their properties.
Solid Geometry
Geometric solid shapes are three-dimensional. The dimensions that are considered: length, width, and height. Figures like cylinders, cubes, spheres, cones, cuboids, prisms, pyramids, and so on are solid figures that take up space. Vertices, faces, and edges characterize them.
Measurement in Geometry
Measurement in geometry involves the calculation of length or distance, the area of a flat shape, and the volume of solid objects. Geometric measurements are used to compute the perimeter, area, capacity, surface area, and volume of geometric figures. A solid’s volume is the amount of area it occupies, and its surface area is the sum of its faces.
Two-dimensional Analytical Geometry
The concept of analytical geometry is the study of the position of any given point on a plane in terms of a rectangular Cartesian coordinate system using ordered pairs of numbers, or coordinates. A coordinate axis divides a plane into four quadrants.
What are some examples of geometry?
1. Nature. The most important example of geometry in everyday life is formed by the nature surrounding humans. If one looks closely, one might find different geometrical shapes and patterns in leaves, flowers, stems, roots, bark, and the list goes on.
What is the meaning of geometry?
The word “Geometry” is derived from the Greek word “Geo” and “Metron” which mean Earth and Measurement respectively. Translating roughly to “Earth’s Measurement,” geometry is primarily concerned with the characteristics of figures as well as shapes. Practically, geometry plays a great role in determining the areas, volumes, and lengths.
How is geometry used in art?
Geometry is widely applied in the field of designing; the creation of animated figures in the video games require geometry. In the case of art, almost every element of designing is entwined with geometric proportions, which is used to depict a story. Taking the examples of miniature paintings and manuscript illumination, geometric principles are employed to compose the layout. Strict geometric proportions are paid attention to while forming individual letters in calligraphy. In designing, geometry has a symbolic role to play; as is evident from the carvings on the walls, roofs, and doors of various architectural marvels.
What sports use geometric shapes?
Sports often does not fail a sole chance to make use of geometrical concepts. The buildings of the sports stadiums and athletic fields take into consideration geometric shapes. The athletic fields also employ geometry; hockey, soccer, basketball, and football fields are rectangular in shape. The corner kick spots, goal posts, arcs, D-section, and centre circle are marked on the field. Similarly, the pitches of various other sports like volleyball and basketball take into consideration the geometrical aspects because these pitches have oval as well as circular arcs marked clearly. Talking of track field, semicircular shapes are often noticeable. Angles also play a critical role in predicting the movement of the players, enhancing their performance, and scoring a point.
Why is geometry important?
Geometry helps in the accurate calculation of the physical distances. It is employed in the field of astronomy to map the distances between stars & planets and between different planets. It also aids in the determination of a relationship between the movements of different bodies in the celestial environment .
What is the relationship between art and geometry?
From the aforesaid, it is evident that there is a close relationship between art and geometry. The formation of shapes is a result of the use of geometrical forms like circle, triangle, square, mandala, or octagon. Moreover, the contents of paintings or sculptures are largely affected by the choice and shape of frames.
What is geometry in architecture?
Geometry, one of the principle concepts of mathematics, entails lines, curves, shapes, and angles. Before any architectural design is made, a computer software helps in rendering visual images on the screen. CAD, a software, puts forth the blueprint of the design.
What is geometrical shape?
Geometrical shapes are the figures which represent the forms of different objects. Some figures are two-dimensional, whereas some are three-dimensional shapes. The two-dimensional figures lie on only x-axis and y-axis, but 3d shapes lie in x, y and z axes. The z-axis shows the height of the object.
What is a shape in geometry?
In geometry, shapes are the forms of objects which have boundary lines, angles and surfaces. There are different types of 2d shapes and 3d shapes. Shapes are also classified with respect to their regularity or uniformity. A regular shape is usually symmetrical such as square, circle, etc. Irregular shapes are asymmetrical.
What is a closed figure?
Hence, a closed figure can be defined as any geometric shape which starts and ends at the same point to form a boundary by line segments or by curves.
What are the two dimensional shapes?
For example, the shape of a tree is irregular or organic. In plane geometry, the two-dimensional shapes are flat shapes and closed figures such as circle, square, rectangle, rhombus, etc. In solid geometry, the three-dimensional shapes are cube, cuboid, cone, sphere and cylinder.
How many edges does a cube have?
A cube is a three-dimensional shape which has 6 faces, 8 vertices and 12 edges. The faces of the cube are square. Example: A Rubik’s cube. Cuboid. A cuboid is also three dimensional solid having 6 faces, 8 vertices and 12 edges but the faces of the cuboid are in a rectangular shape. Example: Matchbox.
What are the two basic shapes that are called polygons?
Geometric shapes such as a square, rectangle, and triangles are few basic 2D shapes. These figures are collectively called polygons. A polygon is any flat shape or plane on a surface of a paper. They have a finite closed boundary made up of a fixed number of line segments and are called sides of the polygon.
What is a point in a line segment?
By definition, a line segment is a part of a line in which a narrow lane is connecting two points within a line. Different numbers of line segments give us different figures and such figures may be either open figure or closed shapes or figures.
What is the definition of geometry?
Geometry Formulas: Geometry is a branch of mathematics that deals with the measurement, properties, and relationships of points, lines, angles, surfaces, and solids. There are two types of geometry – 2D ge ometry or plane geometry and 3D geometry or solid ge ometry. Flat shapes like squares, circles, and triangles are a part of flat geometry and are called 2D shapes. These shapes have only two dimensions, the length and the width.
What are geometric formulas used for?
They are used to work out the length, perimeter, area, and volume of different geometric forms and figures. Numerous geometric formulas deal with height, breadth, length, radius, perimeter, area, surface area or volume, ...
How to find perimeter of a quadrilateral?
If the lengths of the sides of a triangle are a, b, c and d units then. Perimeter = (a + b + c + d)units.
What are two dimensional shapes?
Two-dimensional shapes, like squares, circles, and triangles, are flat shapes with only two dimensions: length and width. Three-dimensional objects are solid objects that have three dimensions, length, width, and height or depth, as in a cube, cuboid, sphere, cylinder, or cone. In this article, we will discuss important geometry formulas.
What is the perimeter of a triangle?
The perimeter of a triangle: The sum of the lengths of sides of a triangle is called its perimeter. If the lengths of the sides of a triangle are a, b and c, then, The perimeter of a triangle is generally denoted by 2s, where s is the semi-perimeter of the triangle. Thus, 2s = (a + b + c)units.
What is the formula for an equilateral triangle?
Areaofanequilateraltriangle = √3 4 a2squnits, where a is the side of an equilateral triangle. Heron’s formula: Heron of Alexandria was the first to discover Heron’s formula.
Geometry in Nature
Math can be applied to almost everything in the real world. Some of it can be quite obvious, like counting fruit or adding and subtracting money. However, math also appears in less obvious ways, such as in shapes. This type of math is called geometry, and it deals primarily with lines, angles, and shapes.
Types of Geometric Shapes in Nature
Shapes are all around and can take many different forms. As previously mentioned, shapes can be 2-D or 3-D. Shapes that are 2-D fall under the category of plane geometry, while 3-D shapes are a type of geometry known as spatial geometry.
Plane Geometry
These are flat shapes, like paper. These shapes include rectangles, hexagons, squares, and triangles. There are plenty of objects in natural life with plane geometry. For example, starfish have flat stars, which is a type of plane geometry. Trees also contain plane geometry on the inside of their trunks.
Why is geometry important in the real world?
Knowing the geometry of objects and things in the real world is a very useful skill. Architects use geometry to aid them in designing buildings and cities that work. Engineers use geometry to build working components in a bigger machine. Create an account.
What is the geometry of space?
The geometry of space is defined by the three dimensions that all objects have in the real world. The geometry of space is used in architecture and engineering to make sure all parts of a bigger object fit together as needed. Problems involving geometry of space most often deal with how much space various objects take up.
What are the dimensions of space?
It involves three dimensions: a length, a width, and a height. Every single object in space has all three of these dimensions. But not all objects are simple block shapes with just one length, one width, and one height. Some objects vary in length, width, and height in different parts of the object. For example, the honeycomb pattern of ...

Geometry Definition
Branches of Geometry
- The branches of geometry are categorized as: 1. Algebraic geometry 2. Discrete geometry 3. Differential geometry 4. Euclidean geometry 5. Convex geometry 6. Topology
Geometry Formulas
- To calculate the area, perimeter, volume and different measures using length, breadth and height of different geometrical figures, geometry formulas are important. By using the formulas, we can calculate the measures easily. There are loads of formulas to learn in Geometry. Here, you are provided with all the important geometry formulas in the PDF. Download the below-given PDF to …
Plane Geometry
- Plane Geometry deals with flat shapes which can be drawn on a piece of paper. These include lines, circles & triangles of two dimensions. Plane geometry is also known as two-dimensional geometry. All the two-dimensional figures have only two measures such as length and breadth. It does not deal with the depth of the shapes. Some examples of plane figures are square, triangle…
Angles in Geometry
- In planar geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Polygons in Geometry
- A plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed polygonal chain or circuit. The name ‘poly’ refers to multiple. An n-gon is a polygon with n sides; for example, a triangle is a 3-gon polygon. General Formula for Sum of internal Angles of a polygon – Sum of internal Angles of a polygon =
Circle in Geometry
- A Circle is a simple closed shape. From a certain point called the centre, all points of a circle are of same consistent distance, i.e. the curve traced out by a point that moves so that its distance from the centre is constant.
Similarity and Congruency in Geometry
- Similarity– Two figures are said to be similar if they have the same shape or have an equal angle but do not have the same size. Congruence– Two figures are said to be Congruent if they have the same shape and size. Thus, they are totally equal.
Solid Geometry
- Solid Geometrydeals with 3-dimensional objects like cubes, prisms, cylinders & spheres. It deals with three dimensions of the figure such as length, breadth and height. But some solid solids do not have faces (e.g. sphere). Solid geometry is the study of three dimensions in Euclidean space. The objects which are around us are three-dimensional. All the three-dimensional shapes are ob…
What Are The Essential Components of Geometric Shapes?
- The most essential elements are flat shapes which can be represented in a piece of paper because they are bi-dimensional objects. They are composed of points, lines, angles, and surfaces. Depending on the type of shape, line segments can be straight lines in the case of polygons or curved.
Examples of Geometry in Everyday Life
- Geometric figures appear in many aspects of everyday life. Here are some examples: 1. In the kitchen, geometric shapes appear among kitchen utensils such as cups, plates, and pans. Chefs need to measure and weigh ingredients to adjust the quantities and volumes of ingredients to use. 2. Video games use geometry to give the sensation of depth and mo...
Evolution of Geometry in History
- The ancient Greeks who were particularly interested in constructing geometric elements of space were already known. The compass and a ruler without a scale were the classic instruments to study geometric figures. In this way, the lengths and areas of the figures could be represented with numerical values. However, these means do not solve all the problems presented due to th…