What is Angle Bisector Theorem?
| Theorem | Statement |
| Internal angle bisector theorem | The angle bisector of a triangle divides ... |
| Converse of Internal angle bisector theo ... | In a triangle, if the interior point is ... |
| Perpendicular bisector theorem | The perpendicular bisector bisects the g ... |
| External angle bisector theorem | The external angle bisector divides the ... |
What is internal and external angle bisector?
The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle.
What is the angle bisector theorem formula?
According to the angle bisector theorem, PQ/PR = QS/RS or a/b = x/y. An angle bisector is a line or ray that divides an angle in a triangle into two equal measures.
What does the angle bisector theorem tell us?
In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
What is external angle bisector theorem?
Exterior angle bisector theorem : The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. Given : A ΔABC, in which AD is the bisector of the exterior ∠A and intersects BC produced in D. Prove that : BD / CD = AB / AC.
How do you find the external bisector?
0:005:48External Bisector of angle of triangle divides opposite side in ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd this property reads as under the external bisector of an angle of a triangle divides theMoreAnd this property reads as under the external bisector of an angle of a triangle divides the opposite side externally note this word this is important in the ratio of sides containing. The angle.
What is acute angle theorem?
The hypotenuse angle theorem, also known as the HA theorem, states that 'if the hypotenuse and an acute angle of one right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent. '
Is median and angle bisector same?
A median of a triangle is a segment connecting a vertex to the midpoint of its opposite side. An altitude of a triangle is a segment from a vertex to the line containing its opposite side, and is perpendicular to that line. An angle bisector divides an angle into two congruent angles.
What is the formula for 30 60 90 triangle?
The sides of a 30-60-90 triangle are always in the ratio of 1:√3: 2. This is also known as the 30-60-90 triangle formula for sides y: y√3: 2y. Let us learn the derivation of this ratio in the 30-60-90 triangle proof section. This formula can be verified using the Pythagoras theorem.
What is the angle bisector of angle ABC?
Construction of Angle Bisector Step 1: Draw any angle, say ∠ABC. Step 3: Now, taking D and E as centers and with the same radius as taken in the previous step, draw two arcs to intersect each other at F. Step 4: Join B to F and extend it as a ray. This ray BF is the required angle bisector of angle ABC.
How do you find the length of the angle bisector of a triangle?
The length of the angle bisector of a standard triangle such as AD in figure 1.1 is AD2 = AB · AC − BD · DC, or AD2 = bc [1 − (a2/(b + c)2)] according to the standard notation of a triangle as it was initially proved by an extension of the angle bisector up to the circumcircle of the triangle.
What is the perpendicular bisector of a line segment?
According to the perpendicular bisector theorem, if a point is equidistant from the endpoints of a line segment in a triangle , then it is on the perpendicular bisector of the line segment.
What type of triangles does the Angle Bisector theorem apply to?
Angle bisector theorem applies to all types of triangles, such as equilateral triangles, isosceles triangles, and right-angled triangles, etc.
How does the angle bisector theorem help in finding unknown lengths of sides of triangles?
The Angle Bisector Theorem helps in finding unknown lengths of sides of triangles because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangle’s other two sides.
What is the bisector theorem?
Angle Bisector Theorem: Proofs and Solved Examples. Angle Bisector Theorem is one of the fundamental theorems in mathematics, especially in geometry. The Angle Bisector Theorem says that an angle bisector of a triangle will divide the opposite side into two proportional segments to the other two sides of the triangle.
What is the line A D?
D is a point in the interior of angle ∠ B A C. If the perpendicular distances | D C | and | D B | are equal then, the line A D is the angle bisector of angle ∠ B A C.
What is an angle bisector?
An angle bisector is a ray or line which divides the given angle into two congruent angles. The properties of an angle bisector are given below: 1. Any point on the bisector of an angle is equidistant from the sides of the angle. 2.
What is the internal angle bisector?
Internal Angle Bisector Theorem. An angle bisector of a triangle divides the opposite side into two segments proportional to the other two sides of the triangle. In the triangle ABC, the angle bisector intersects side BC at point D.
What is the bisector of a triangle?
An angle bisector of a triangle divides the interior angle's opposite side into two segments that are proportional to the other two sides of the triangle.
What is the angle bisector?
Angle Bisector Definition. The Angle Bisector Theorem helps you find unknown lengths of sides of triangles, because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangle's other two sides.
What is a linear object?
The linear object is an angle bisector. When it crossed side a a opposite ∠A ∠ A, it divided △ ABC △ A B C into two smaller triangles and divided side a a in two.
How many years has Malcolm been a teacher?
Malcolm has a Master's Degree in education and holds four teaching certificates. He has been a public school teacher for 27 years, including 15 years as a mathematics teacher.
How many meters is BA B A?
Using cross multiplication ( 25 × 20 = 500 25 × 20 = 500) and then division ( 500 10 500 10) , we get BA B A = 50 meters.
What are the properties of the angle bisector?
Ans: The properties of the angle bisector of a triangle are: 1. Any point on the bisector of an angle is equidistant from the sides of the angle. 2. In a triangle, the angle bisector divides the opposite side in the ratio of the adjacent sides. Q.4.
What is the internal bisector angle?
Theorem 1: The internal angle bisector of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
What is the bisector of an angle of a triangle?
The bisector of a triangle that divides the opposite side internally in the ratio of corresponding sides containing angles is known as the internal bisector of an angle of a triangle.
What is the line segment that bisects one of the vertex angles of a triangle and ends up?
A line segment that bisects one of the vertex angles of a triangle and ends up on the corresponding side of a triangle is known as the angle bisector of a triangle. There are three angle bisectors in a triangle. The bisectors of a triangle meet in a single point called the incentre. This point is always inside the triangle.
What is the name of the ray that divides an angle into two equal measures?
A ray that divides a given angle into two angles with equal measures is called an angle bisector. We usually divide an angle or an angle in a triangle by a line or ray, which is considered an angle bisector. Bisecting an angle means drawing a ray in the interior of the angle, with its initial point at the vertex of the angle such ...
How many equal angles does an angle bisector divide?
Example: Consider an angle ∠ A B C = 80 ∘. An angle bisector divides it into two equal angles of 40 ∘.
What is the bisector of a line?
In geometry, a bisector is applied to the line segment s and angles. A line that passes through the midpoint of a line segment is known as the bisector of the line segment. The line that passes through the vertex of an angle bisecting is known as the angle bisector. In this article, let us discuss the definition of an angle bisector, ...
What is the angle bisector theorem?
The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
What does it mean to bisect an angle?
To bisect an angle means to cut it into two equal parts or angles. Say that we wanted to bisect a 50-degree angle, then we would divide it into two 25-degree angles.
What is the immediate consequence of the theorem?
An immediate consequence of the theorem is that the angle bisector of the vertex angle of an isosceles triangle will also bisect the opposite side.
What is the angle bisector theorem?
In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
What is AD in triangles?
and conversely, if a point D on the side BC of triangle ABC divides BC in the same ratio as the sides AB and AC, then AD is the angle bisector of angle ∠ A .
What happens when a triangle is divided internally?
If an angle of a triangle is bisected internally or externally by a straight line which cuts the opposite side or the opposite side produced, the segments of that side will have the same ratio as the other sides of the triangle; and, if a side of a triangle be divided internally or externally so that its segments have the same ratio as the other sides of the triangle, the straight line drawn from the point of section to the angular point which is opposite to the first mentioned side will bisect the interior or exterior angle at that angular point.
Is ADB supplementary to ADC?
Angles ∠ ADB and ∠ ADC are still supplementary, so the right hand sides of these equations are still equal, so we obtain:
What is the bisector of an angle?
The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle. To know more about proof, please visit the page "Angle bisector theorem proof". Example 1 :
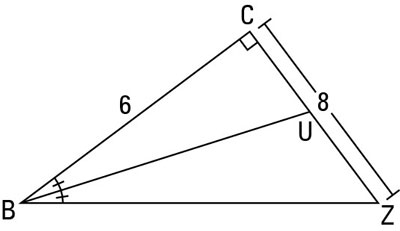
What is MP in a triangle?
In a triangle MNO, MP is the external bisector of angle M meeting NO produced at P. IF MN = 10 cm, MO = 6 cm, NO - 12 cm, then find OP.
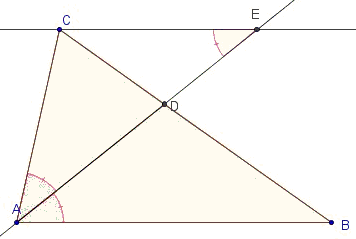
Where does the internal bisector of a triangle ABC meet BC?
The internal bisector of ∠A of triangle ABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that (BD/BE) = (CD/CE).
Is ABCD a quadrilateral?
ABCD is a quadrilateral with AB = AD. If AE and AF are internal bisectors of ∠BAC and ∠DAC respectively,then prove that the sides EF and BD are parallel.
Can you replace AB with AD?
Since lengths of AD and AB are equal, we may replace AB instead of AD.
What Is Angle Bisector Theorem?
Converse of Angle Bisector Theorem
- In a triangle, if the interior point is equidistant from the two sides of a triangle then that point lies on the angle bisector of the angle formed by the two line segments.
Triangle Angle Bisector Theorem
- Extend the side CA to meet BE to meet at point E, such that BE//AD. Now we can write, CD/DB = CA/AE (since AD//BE) —-(1) ∠4 = ∠1 [corresponding angles] ∠1 = ∠2 [AD bisects angle CAB] ∠2 = ∠3 [Alternate interior angles] ∠3 = ∠4 [By transitive property] ΔABE is an isosceles triangle with AE=AB Now if we replace AE by AB in equation 1, we get; CD/DB = CA/AB Hence proved.
Perpendicular Bisector Theorem
- According to this theorem, if a point is equidistant from the endpoints of a line segment in a triangle, then it is on the perpendicular bisector of the line segment. Alternatively, we can say, the perpendicular bisector bisects the given line segment into two equal parts, to which it is perpendicular. In the case of a triangle, if a perpendicular bisector is drawn from the vertex to th…
External Angle Bisector Theorem
- The external angle bisector of a triangle divides the opposite side externally in the ratio of the sides containing the angle. This condition occurs usually in non-equilateral triangles.
Solved Examples on Angle Bisector Theorem
- Go through the following examples to understand the concept of the angle bisector theorem. Example 1: Find the value of x for the given triangle using the angle bisector theorem. Solution: Given that, AD = 12, AC = 18, BC=24, DB = x According to angle bisector theorem, AD/AC = DB/BC Now substitute the values, we get 12/18 = x/24 X = (⅔)24 x = 2(8) x= 16 Hence, the value of x is …
Definition and Statement of Angle Bisector Theorem
Angle Bisector
- An angle bisector is a ray or line which divides the given angle into two congruent angles. The properties of an angle bisector are given below: 1. Any point on the bisector of an angle is equidistant from the sides of the angle. 2. In a triangle, the angle bisector divides the opposite side in the ratio of the adjacent sides.
Construction of Angle Bisector
- Follow the steps given below for constructing an angle bisector with an example 1. Step \(1:\) Draw any angle, say \(\angle ABC\). 2. Step \(2:\) Taking \(B\) as the centre and any appropriate radius, draw an arc to intersect the rays \(BA\) and \(BC\) at, say, \(E\) and \(D,\) respectively. 3. Step \(3:\) Now, taking \(D\) and \(E\) as centres and with a radius more than hal…
Internal Angle Bisector Theorem
- An angle bisector of a triangle divides the opposite side into two segments proportional to the other two sides of the triangle. In the triangle \(ABC,\) the angle bisector intersects side \(BC\) at point \(D.\) As per the angle bisector theorem, the ratio of the line segment \(BD\) to \(DC\) is equal to the ratio of the length of the side \(AB\) t...
External Angle Bisector Theorem
- The external angle bisector of a triangle divides the opposite side externally in the ratio of the sides containing the angle. This condition usually occurs in non-equilateral triangles. In the triangle \(ABC, AD\) is the internal bisector of \(∠BAC,\) which meets \(BC\) at \(D.\) According to the angle bisector theorem, the ratio of the line segment \(BD\) to \(DC\) equals the ratio of the l…
Converse of Angle Bisector Theorem
- If a point lies on the interior of an angle and is equidistant from the angle’s sides, then a line from the angle’s vertex through the point bisects the angle. \(D\) is a point in the interior of angle \(∠BAC.\) If the perpendicular distances \(\left| {DC} \right|\) and \(\left| {DB} \right|\) are equal then, the line \(AD\) is the angle bisector of angle \(∠BAC.\) \(\angle BAD \cong \angle CAD\)
Perpendicular Bisector Theorem
- According to the perpendicular bisector theorem, if a point is equidistant from the endpoints of a line segment in a triangle, then it is on the perpendicular bisector of the line segment. Compare \(ΔAPM\) and \(ΔBPM.\) We have: 1. \(AM=BM\) 2. \(PM=PM\) (common) 3. \(\angle AMP = \angle BMP = {90^{\rm{o}}}\) We see that \(ΔAPM≅ΔBPM\) by the \(SAS\) congruence c…
Solved Examples – Angle Bisector Theorem
- Q.1. In \(∆ABC,\)if \(AD\)bisects \(BAC.\)Find the value of \(x\)? Ans: Given that, \(AD\) is the bisector of \(∠A.\) According to the angle bisector theorem: \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\) \( \Rightarrow \frac{x}{{x – 2}} = \frac{{x + 2}}{{x – 1}}\) \( \Rightarrow x(x – 1) = (x – 2)(x + 2)\) \( \Rightarrow {x^2} – x = {x^2} – 4\) \( \Rightarrow – x = – 4\) \( \Rightarrow x …
Summary
- The angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle. In this article, we have discussed the most important theorems on the angle bisector. We have learnt about the angle bisector theorem proof, angle bisector theorem examples, triangle angle bisector theorem, perpendicular angle bisector theorem, how to construct angle bisector, …
Frequently Asked Questions
- Q.1. What is an example of a perpendicular bisector? Ans:The median of a triangle is the line that joins the vertex of the triangle to the midpoint of the opposite side of the vertex. The median of an equilateral triangle is an example of a perpendicular bisector. Q.2. What is an angle bisector of a triangle? Ans:An angle bisector is nothing but a ray that divides an angle into two congruent part…
Angle Bisector Theorem
- Bisector means the elements that bisect a given shape or an object into two identical parts and an angle is developed when two straight linesor rays meet at a common endpoint. The angle bisector theorem says that an angle bisector of a triangle divides/splits the opposite side of the triangle into two elements such that they are proportional to the other two sides of the triangle. Or you c…
Types of Angle Bisector Theorem
- As of now, we know what is angle bisector theorem through its definition. Let us understand the two different types of it. 1. Interior Angle Bisector Theorem 2. Exterior Angle Bisector Theorem
Formula of Angle Bisector Theorem
- As per the statement, we can say that the internal or external bisector of an angle in a triangle divides or splits the opposite side internally or externally in the ratio of the corresponding sides having the angle. For the diagram below in the triangle ABC, AD is the bisector, then the angle bisector theorem formula is;BDDC=ABAC
Angle Bisector Theorem Proof
- Now that we know the internal as well as the external angle bisector theorem with the formula, let us understand the proof for the same.
Angle Bisector Theorem Converse
- The converse of the angle bisector theorem states that if a given triangle satisfies the below condition; Condition: if a line sketched from one vertex of the triangle splits the opposing side into two portions such that they are symmetrical to the rest two sides of the triangle. Conclusion: If the above statement is true then the point on the opposite side of the angle will lie on the angle bise…
Solved Examples of Angle Bisector Theorem
- The angle bisector theorem enables us to determine the unknown lengths of sides of triangles as the angle bisector separates the side opposite to the angle into two segments such that they are proportional to the triangle’s other two sides. With all this information below are some practice questions, try to solve them on your own and check your answer. Solved Example 1: For the give…
Table of Contents
Angle Bisector Definition
How to Construct An Angle Bisector
Angle Bisector Theorem
- Here is one version of the Angle Bisector Theorem: An angle bisector of a triangledivides the interior angle's opposite side into two segments that are proportional to the other two sides of the triangle. Angle bisector ADAD cuts side aa into two line segments, CDCD and DBDB. CDCD and DBDB relate to sides bb (CACA) and cc (BABA) in the same proport...
Ratios & Proportions
Angle Bisector Examples
Angle Bisector of A Triangle
Lesson Summary