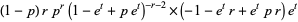
How to calculate binomial distribution?
- First, use the sliders (or the plus signs +) to set n = 5 and p = 0.2. ...
- Then, as you move the sample size slider to the right in order to increase n, notice that the distribution moves from being skewed to the right to approaching symmetry.
- Now, set p = 0.5. ...
How to find probability using binomial distribution?
To use the binomial distribution table, you only need three values:
- n: the number of trials
- r: the number of “successes” during n trials
- p: the probability of success on a given trial
How do you find the probability between two numbers?
- z a / 2 : Divide the confidence level by two, and look that area up in the z-table: .95 / 2 = 0.475. …
- E (margin of error): Divide the given width by 2. 6% / 2. …
- : use the given percentage. 41% = 0.41. …
- : subtract. from 1.
What is binomial distribution and its properties?
So, let us come to know the properties of binomial distribution. Properties of binomial distribution. 1. Binomial distribution is applicable when the trials are independent and each trial has just two outcomes success and failure. It is applied in coin tossing experiments, sampling inspection plan, genetic experiments and so on. 2. Binomial distribution is known as bi-parametric distribution as it is characterized by two parameters n and p.

What is K in a binomial distribution?
The probability that a random variable X with binomial distribution B(n,p) is equal to the value k, where k = 0, 1,....,n , is given by , where . The latter expression is known as the binomial coefficient, stated as "n choose k," or the number of possible ways to choose k "successes" from n observations.
What is the formula of negative binomial distribution?
A random variable X is supposed to follow a negative binomial distribution if its probability mass function is given by: f(x) = (n + r - 1)C(r - 1) Prx. Here we consider a binomial sequence of trials with the probability of success as p and the probability of failure as q.
How do you find K in binomial probability?
0:095:01Determine Binomial Probabilities Using Formulas: P(x=k) - YouTubeYouTubeStart of suggested clipEnd of suggested clipBelow the probability that x is equal to k is equal to n choose k times p raised to the power of k.MoreBelow the probability that x is equal to k is equal to n choose k times p raised to the power of k. Times the quantity one minus p raised to the power of n minus k.
What are the parameters in negative binomial distribution?
The Probability Density Function The distribution defined by the density function in (1) is known as the negative binomial distribution ; it has two parameters, the stopping parameter k and the success probability p.
What is the mean and variance of negative binomial?
The mean of the negative binomial distribution with parameters r and p is rq / p, where q = 1 – p. The variance is rq / p2. The simplest motivation for the negative binomial is the case of successive random trials, each having a constant probability P of success.
What is n in binomial distribution?
The first variable in the binomial formula, n, stands for the number of times the experiment runs. The second variable, p, represents the probability of one specific outcome.
What is p and Q in binomial distribution?
p = the probability of a success for any trial. q = the probability of a failure for any trial.
How do you find the expected value?
To find the expected value, E(X), or mean μ of a discrete random variable X, simply multiply each value of the random variable by its probability and add the products. The formula is given as E ( X ) = μ = ∑ x P ( x ) .
What does negative binomial distribution tell us?
The negative binomial distribution, like the normal distribution, is described by a mathematical formula. The negative binomial distribution is commonly used to describe the distribution of count data, such as the numbers of parasites in blood specimens, where that distribution is aggregated or contagious.
What is negative binomial distribution with example?
Example: Take a standard deck of cards, shuffle them, and choose a card. Replace the card and repeat until you have drawn two aces. Y is the number of draws needed to draw two aces. As the number of trials isn't fixed (i.e. you stop when you draw the second ace), this makes it a negative binomial distribution.
How do you calculate negative binomial distribution in r?
0:032:52Negative Binomial Distributions in R - YouTubeYouTubeStart of suggested clipEnd of suggested clipFor the negative binomial distribution. The command that we need is d in binome. And then we needMoreFor the negative binomial distribution. The command that we need is d in binome. And then we need three variables X R and P.
Where is the negative binomial distribution used?
The negative binomial distribution is a probability distribution that is used with discrete random variables. This type of distribution concerns the number of trials that must occur in order to have a predetermined number of successes.
Why is it called a negative binomial distribution?
The term "negative binomial" is likely due to the fact that a certain binomial coefficient that appears in the formula for the probability mass function of the distribution can be written more simply with negative numbers.
What is negative binomial distribution?
The negative binomial distribution is a probability distribution that is used with discrete random variables. This type of distribution concerns the number of trials that must occur in order to have a predetermined number of successes. As we will see, the negative binomial distribution is related to the binomial distribution . In addition, this distribution generalizes the geometric distribution.
What is the probability mass function for a negative binomial distribution?
The probability mass function for a negative binomial distribution can be developed with a little bit of thought. Every trial has a probability of success given by p . Since there are only two possible outcomes, this means that the probability of failure is constant (1 - p ).
What is the geometric random variable X?
A geometric random variable X counts the number of trials necessary before the first success occurs. It is easy to see that this is exactly the negative binomial distribution, but with r equal to one.
Why is the mean of a distribution important?
The mean of a distribution is important to know because it is one way to denote the center of the distribution. The mean of this type of random variable is given by its expected value and is equal to r / p . We can prove this carefully by using the moment generating function for this distribution.
Is a negative binomial distribution a geometric distribution?
In addition to this connection, the negative binomial distribution is a more general version of a geometric distribution.
What is the negative binomial distribution?
For k + r Bernoulli trials with success probability p, the negative binomial gives the probability of k successes and r failures, with a failure on the last trial. In other words, the negative binomial distribution is the probability distribution of the number of successes before the r th failure in a Bernoulli process, with probability p of successes on each trial. A Bernoulli process is a discrete time process, and so the number of trials, failures, and successes are integers.
What is negative binomial?
The negative binomial, along with the Poisson and binomial distributions, is a member of the (a,b,0) class of distributions. All three of these distributions are special cases of the Panjer distribution. They are also members of the Natural exponential family .
How to find the expected total number of successes in a negative binomial distribution?
The expected total number of successes in a negative binomial distribution with parameters (r, p) is rp / (1 − p ). To see this, imagine an experiment simulating the negative binomial is performed many times. That is, a set of trials is performed until r failures are obtained, then another set of trials, and then another etc. Write down the number of trials performed in each experiment: a, b, c, … and set a + b + c + … = N. Now we would expect about Np successes in total. Say the experiment was performed n times. Then there are nr failures in total. So we would expect nr = N(1 − p), so N/n = r/ (1 − p). See that N/n is just the average number of trials per experiment. That is what we mean by "expectation". The average number of successes per experiment is N/n − r = r/ (1 − p) − r = rp/ (1 − p). This agrees with the mean given in the box on the right-hand side of this page.
What is the sum of independent negative binomially distributed random variables?
The sum of independent negative-binomially distributed random variables r1 and r2 with the same value for parameter p is negative-binomially distributed with the same p but with r -value r1 + r2 .
Which binomial distribution converges to Poisson?
In other words, the alternatively parameterized negative binomial distribution converges to the Poisson distribution and r controls the deviation from the Poisson. This makes the negative binomial distribution suitable as a robust alternative to the Poisson, which approaches the Poisson for large r, but which has larger variance than the Poisson for small r .
What is the definition of X in statistics?
The definition where X is the number of n trials that occur for a given number of r successes. This definition is very similar to definition #2, only that r successes is given instead of k failures. Note however, that p still refers to the probability of "success".
Why are there k failures chosen from k+r-1 samples rather than k+r?
There are k failures chosen from k+r-1 samples rather than k+r because the last of the k+r samples is by definition a success.

The Setting
Example
- To help make sense of a negative binomial distribution, it is worthwhile to consider an example. Suppose that we flip a fair coin and we ask the question, "What is the probability that we get three heads in the first X coin flips?" This is a situation that calls for a negative binomial distribution. The coin flips have two possible outcomes, the probability of success is a constant 1/2, and the …
Probability Mass Function
- The probability mass function for a negative binomial distribution can be developed with a little bit of thought. Every trial has a probability of success given by p. Since there are only two possible outcomes, this means that the probability of failure is constant (1 - p ). The rth success must occur for the xth and final trial. The previous x - 1 trials must contain exactly r - 1 successes. Th…
The Name of The Distribution
- We are now in a position to understand why this random variable has a negative binomial distribution. The number of combinations that we encountered above can be written differently by setting x - r = k: (x - 1)!/[(r - 1)!(x - r)!] = (x + k - 1)!/[(r - 1)!k!] = (r + k - 1)(x + k - 2) . . . (r + 1)(r)/k! = (-1)k(-r)(-r - 1). . .(-r -(k + 1)/k!. Here...
Mean
- The mean of a distribution is important to know because it is one way to denote the center of the distribution. The mean of this type of random variable is given by its expected value and is equal to r / p. We can prove this carefully by using the moment generating functionfor this distribution. Intuition guides us to this expression as well. Suppose that we perform a series of trials n1 until …
Variance
- The variance of the negative binomial distribution can also be calculated by using the moment generating function. When we do this we see the variance of this distribution is given by the following formula: r(1 - p)/p2
Moment Generating Function
- The moment generating function for this type of random variable is quite complicated. Recall that the moment generating function is defined to be the expected value E[etX]. By using this definition with our probability mass function, we have: M(t) = E[etX] = Σ (x - 1)!/[(r - 1)!(x - r)!]etXpr(1 - p)x- r After some algebra this becomes M(t) = (pet)r[1-(1- p)et]-r
Relationship to Other Distributions
- We have seen above how the negative binomial distribution is similar in many ways to the binomial distribution. In addition to this connection, the negative binomial distribution is a more general version of a geometric distribution. A geometric random variable X counts the number of trials necessary before the first success occurs. It is easy to see that this is exactly the negative …
Example Problem
- We will look at an example problem to see how to work with the negative binomial distribution. Suppose that a basketball player is an 80% free throw shooter. Further, assume that making one free throw is independent of making the next. What is the probability that for this player the eighth basket is made on the tenth free throw? We see that we have a setting for a negative binomial di…
Overview
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures (denoted r) occur. For example, we can define rolling a 6 on a die as a failure, and rolling any other number as a success, and ask how many successful rolls will occur before we see the third failure (r = 3). In s…
Definitions
Suppose there is a sequence of independent Bernoulli trials. Each trial has two potential outcomes called "success" and "failure". In each trial the probability of success is p and of failure is (1 − p). We observe this sequence until a predefined number r of successes have occurred. Then the random number of failures we have seen, X, will have the negative binomial (or Pascal) distribution:
Properties
The expected total number of successes in a negative binomial distribution with parameters (r, p) is rp/(1 − p). To see this, imagine an experiment simulating the negative binomial is performed many times. That is, a set of trials is performed until r failures are obtained, then another set of trials, and then another etc. Write down the number of trials performed in each experiment: a, b, c, ... and set a + b + c + ... = N. Now we would expect about Np successes in total. Say the experim…
Related distributions
• The geometric distribution (on { 0, 1, 2, 3, ... }) is a special case of the negative binomial distribution, with
• The negative binomial distribution is a special case of the discrete phase-type distribution.
• The negative binomial distribution is a special case of discrete Compound Poisson distribution.
Statistical inference
Suppose p is unknown and an experiment is conducted where it is decided ahead of time that sampling will continue until r successes are found. A sufficient statistic for the experiment is k, the number of failures.
In estimating p, the minimum variance unbiased estimator is
When r is known, the maximum likelihood estimate of p is
Occurrence and applications
For the special case where r is an integer, the negative binomial distribution is known as the Pascal distribution. It is the probability distribution of a certain number of failures and successes in a series of independent and identically distributed Bernoulli trials. For k + r Bernoulli trials with success probability p, the negative binomial gives the probability of k successes and r failures, with a failure on the last trial. In other words, the negative binomial distribution is the probability …
History
This distribution was first studied in 1713, by Montmort, as the distribution of the number of trials required in an experiment to obtain a given number of successes. It had previously been mentioned by Pascal.
See also
• Coupon collector's problem
• Beta negative binomial distribution
• Extended negative binomial distribution
• Negative multinomial distribution