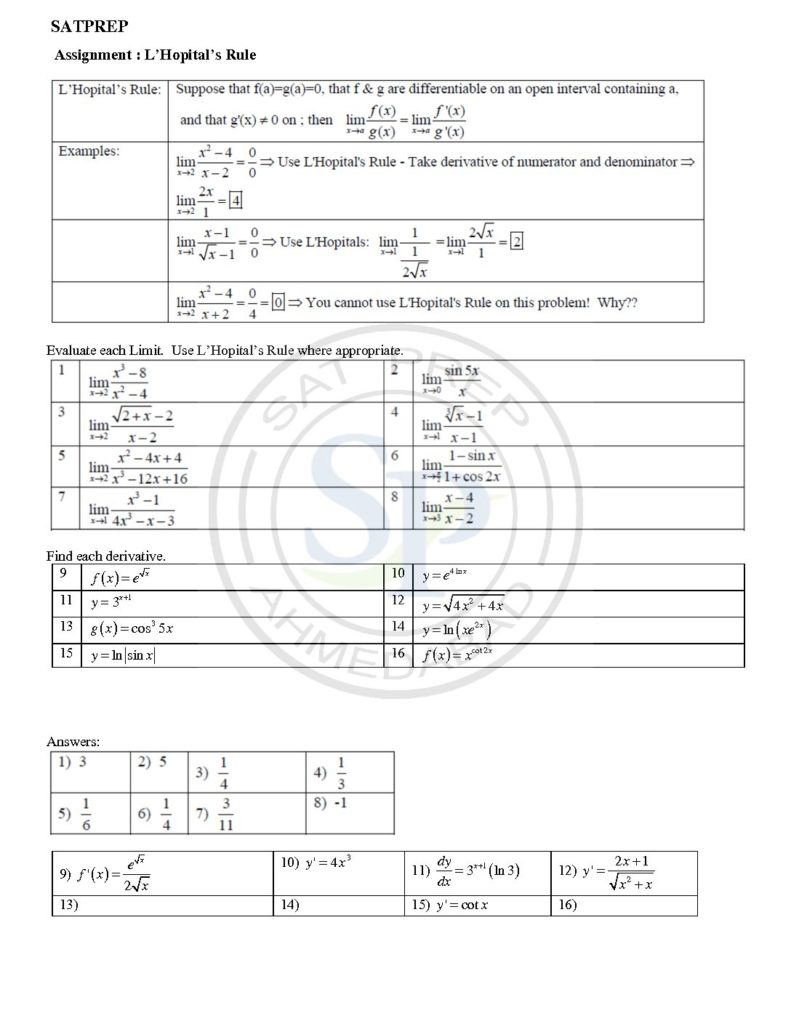
L'Hopital's Rule
- If f (x) and g ( x) are differentiable functions and
- f ( a) = g ( a) = 0, then
- if the limit on the right exists.
What is an example of L'Hopital's rule in calculus?
We have already seen a 0 0 and ∞ ∞ example. Here are all the indeterminate forms that L'Hopital's Rule may be able to help with: For a limit approaching c, the original functions must be differentiable either side of c, but not necessarily at c. Likewise g’ (x) is not equal to zero either side of c.
What is l’Hôpital’s rule?
L’Hôpital’s Rule provides a method for evaluating such limits. We will denote lim x → a, lim x → a +, lim x → a −, lim x → ∞, and lim x → − ∞ generically by lim in what follows. Suppose lim f ( x) = lim g ( x) = 0.
Can I use l'Hôpital's rule to evaluate limits?
The proof is a good example of how the Mean Value Theorem can be used to prove other important ideas, but (to be honest) if you don't read or understand the proof of L'Hôpital's Rule, it won't hinder your ability to use it to evaluate limits. So, you can skip it if necessary (it is a really pretty proof, though.
Does l'Hôpital's rule apply to infinity?
So that new limit does not exist! And so L'Hôpital's Rule is not usable in this case. As x goes to infinity then cos (x) x tends to between −1 ∞ and +1 ∞, and both tend to zero.

What is L Hopital's Rule example?
L'Hospital's Rule Examples (2 sin x – sin 2x) / (x – sin x) = 6.
Where do I apply for L Hospital rule?
Solution: both numerator and denominator have limit 0, so we are entitled to apply L'Hospital's rule: limx→0sinxx=limx→0cosx1. In the new expression, neither numerator nor denominator is 0 at x=0, and we can just plug in to see that the limit is 1.
How do you solve limits with L Hopital's rule?
0:304:03Solving limits with L'Hopital's rule - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe can solve such a limit using l'hopital's rule but there are two conditions. The first one is thatMoreWe can solve such a limit using l'hopital's rule but there are two conditions. The first one is that for X tends to a f of X should tend to 0. And also G of X should tend to 0. So we will get
Who made L Hopital's rule?
John (Johann) BernoulliL'Hospital's Rule was first published in 1696 in the Marquis de l'Hospital's calculus textbook Analyse des Infiniment Petits, but the rule was discovered in 1694 by the Swiss mathematician John (Johann) Bernoulli.
Is L'Hôpital's rule a magic bullet?
Sometimes L'Hôpital's Rule has to be applied more than once in order to find the limit value. This rule is NOT a magic-bullet. There are some situations where the rule fails to produce a usable solution.
Does L'Hôpital's rule work with every limit?
It is important to note that L'Hôpital's rule is one tool in our toolbox, but it doesn't help with every limit. In the next lesson we'll look at some examples of limits where applying L'Hôpital's rule isn't appropriate, and we'll discuss what we can do to successfully evaluate such limits.
Example 1
In the graph on the left, the applet shows a graph of This is not defined for x = 0, but it clearly seems to have a limit there.
Example 2
Select the second example from the drop down menu. This shows another example, Again, if you click on Zoom In a few times, the graphs look like straight lines and the ratio can be evaluated just by using the ratio of the values of the derivatives.
Example 3
Select the third example, showing In this case, the limit on the right does not exist, so L'Hopital's Rule cannot be used in this case.