What is the Small Angle Approximation? The small angle approximation tells us that for a small angle θ given in radians, the sine of that angle, sin θ is approximately equal to theta. In mathematical form,
What is small angle approximation in trigonometry?
The small-angle approximation is the term for the following estimates of the basic trigonometric functions, valid when theta approx 0: θ ≈ 0: sin theta approx theta, qquad cos theta approx 1 - frac {theta^2} {2} approx 1, qquad tan theta approx theta. sinθ ≈ θ, cosθ ≈ 1− 2θ2 ≈ 1, tanθ ≈ θ.
What are small-angle approximations?
The small-angle approximations correspond to the low-order approximations of these Taylor series, as can be seen from the expansions above. an (x) \approx x tan(x)≈x. For very small angles (x<0.1), (x< 0.1), the approximation is excellent and the error is very small.
What does it mean to use an approximation?
It's an approximation used when you know an angle is likely to be small - what exactly "small" is depends on how much precision you need. For example, you might have an equation involving \sin ( heta).
What are the relative errors of small angle approximations?
Figure 3 shows the relative errors of the small angle approximations. The angles at which the relative error exceeds 1% are as follows: tan θ ≈ θ at about 0.176 radians (10°). sin θ ≈ θ at about 0.244 radians (14°). cos θ ≈ 1 − θ 22 at about 0.664 radians (38°).
What is meant by small angle approximation in physics?
The small angle approximation is a rule that says that for small angles, the trigonometric functions sine and tangent are approximately equal to the angle. The approximation is valid only when angles are measured in radians.
When can you use small angle approximation?
The Small Angle Approximation can be applied when θ is small (< 10°), or when d >> D (much greater - not just a couple times as large, but a few, 10, even 100+ times as large). The angular sizes of many objects in the sky are small and the Small Angle Approximation can be applied when studying them.
What is considered small for small angle approximation?
0.26 radiansWhen the angle is small (usually less than or equal to 15 degrees or 0.26 radians), small-angle approximation can be used to simplify the three primary trigonometric formulas. It must be noted that these formulas are approximations and are not as accurate as the angle gets bigger.
How do you prove small angle approximation?
5:5410:39Small Angle Approximations (1 of 4: Proof) - YouTubeYouTubeStart of suggested clipEnd of suggested clipYou can still see my x. And my minus x there there we go there's one there's my radius in yellow.MoreYou can still see my x. And my minus x there there we go there's one there's my radius in yellow. And then here's my other radius. Now what i've got here no i am going to put it lower what i've got.
How accurate is small angle approximation?
Error of the approximations The angles at which the relative error exceeds 1% are as follows: cos θ ≈ 1 at about 0.1408 radians (8.07°) tan θ ≈ θ at about 0.1730 radians (9.91°) sin θ ≈ θ at about 0.2441 radians (13.99°)
Is small angle approximation in radians or degrees?
More typically, saying 'small angle approximation' typically means θ≪1, where θ is in radians; this can be rephrased in degrees as θ≪57∘.
Why do we use small angle in simple pendulum?
The reason this approximation works is because for small angles, SIN θ ≈ θ. For small angles (in units of radians) the powers of θ become increasingly smaller, thus the higher order terms in the Taylor series vanish. So we can use the small angle approximation in analyzing the pendulum using Newton's Laws.
Why do we use small angle in simple pendulum?
The reason this approximation works is because for small angles, SIN θ ≈ θ. For small angles (in units of radians) the powers of θ become increasingly smaller, thus the higher order terms in the Taylor series vanish. So we can use the small angle approximation in analyzing the pendulum using Newton's Laws.
How do you use small angle formulas?
1:454:44Small Angle Formula - YouTubeYouTubeStart of suggested clipEnd of suggested clipIt's the arc length divided by the radius of the circle. You could sort of think of this as. The asMoreIt's the arc length divided by the radius of the circle. You could sort of think of this as. The as being the radius of a very large circle that has a radius.
What is small angle approximation pendulum?
Small Angle Approximation and Simple Harmonic Motion With the assumption of small angles, the frequency and period of the pendulum are independent of the initial angular displacement amplitude. All simple pendulums should have the same period regardless of their initial angle (and regardless of their masses).
What is a small angle approximation?
The small-angle approximation also appears in structural mechanics, especially in stability and bifurcation analyses (mainly of axially-loaded columns ready to undergo buckling ). This leads to significant simplifications, though at a cost in accuracy and insight into the true behavior.
Why are approximations used in physics?
One reason for this is that they can greatly simplify differential equations that do not need to be answered with absolute precision.
Which approximation forms the basis of the paraxial approximation?
In optics, the small-angle approximations form the basis of the paraxial approximation .
How to find the tangent of a small angle?
By extension, since the cosine of a small angle is very nearly 1, and the tangent is given by the sine divided by the cosine,
What is the second order of cosine approximation?
The second-order cosine approximation is especially useful in calculating the potential energy of a pendulum, which can then be applied with a Lagrangian to find the indirect (energy) equation of motion.
Taylor Series
Did you see the magical improvement for cos when we went from 1 to 1 − θ2 2 ?
Uses
These approximations are very useful in astronomy where many angles are very small.
What is a small angle approximation?
small angle approximation is used usually to replace non linear trigonometric function by some simpler and more importantly linear equivalent functions. For example if angle is small enough:
When to use "small" approximation?
It's an approximation used when you know an angle is likely to be small - what exactly "small" is depends on how much precision you need.

Overview
The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
These approximations have a wide range of uses in branches of physics and engineering, including mechanics, electromagnetism, optics, cartography, astron…
Justifications
The accuracy of the approximations can be seen below in Figure 1 and Figure 2. As the measure of the angle approaches zero, the difference between the approximation and the original function also approaches 0.
• Figure 1. A comparison of the basic odd trigonometric functions to θ. It is seen that as the angle approaches 0 the approximations become better.
Error of the approximations
Figure 3 shows the relative errors of the small angle approximations. The angles at which the relative error exceeds 1% are as follows:
• cos θ ≈ 1 at about 0.1408 radians (8.07°)
• tan θ ≈ θ at about 0.1730 radians (9.91°)
Specific uses
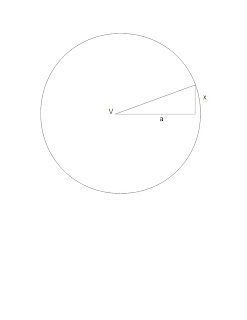
In astronomy, the angular size or angle subtended by the image of a distant object is often only a few arcseconds, so it is well suited to the small angle approximation. The linear size (D) is related to the angular size (X) and the distance from the observer (d) by the simple formula:
where X is measured in arcseconds.
The number 206265 is approximately equal to the number of arcseconds in a circle (1296000), di…
See also
• Skinny triangle
• Infinitesimal oscillations of a pendulum
• Versine and haversine
• Exsecant and excosecant