for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f. All 6 trigonometric functions are periodic functions.
Full Answer
What is the meaning of P in trigonometry?
Suppose the coordinate of a point P on the unit circle is ( x, y). And the angle enclosed by OP and the positive x-axis is θ. When P is in the first quadrant, θ is an acute angle.
What does sin P mean?
The Saskatchewan Immigrant Nominee Program (SINP) is a way to immigrate to Canada. Through the SINP, the Province of Saskatchewan: Invites residency applications from non-Canadians who want to make Saskatchewan their home. Nominates successful applicants to the federal government for permanent residency in Canada.
What is P B in trigonometry?
sine = Perpendicular/hypotenuse(PH) 2. cosine = Base/hypotenuse(BH) 3. tangent = Perpendicular/base(PB)
What is P θ?
It means that the probability is evaluated with θ as the parameter of the distribution.
How do you solve sin Pi?
In trigonometry, we use pi (π) for 180 degrees to represent the angle in radians. Hence, sin π is equal to sin 180 or sin π = 0.
What is the value of sin θ?
The sine of the angle θ is represented by the y-value of the point P on the unit circle. Thus, since sin θ = sin (180 − θ), we mark the two equal intervals in the graph. Hence, between 0° and 180°, the graph is symmetric about θ = 90°. Similarly, between 180° and 360°, the graph is symmetric about θ = 270°.
What are the 3 formulas of trigonometry?
Sine, cosine and tangent are the primary trigonometry functions whereas cotangent, secant and cosecant are the other three functions....The reciprocal trigonometric identities are:Sin θ = 1/Csc θ or Csc θ = 1/Sin θCos θ = 1/Sec θ or Sec θ = 1/Cos θTan θ = 1/Cot θ or Cot θ = 1/Tan θ
Is Trig hard?
Trigonometry is hard because you have to memorize various values of different functions in both degrees and radians. If you don't remember them, or if you mix them up, then your calculations will be incorrect.
What are the 6 formulas of trigonometry?
The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec)....Examples are:Sin 30° = ½Cos 90° = 0.Tan 45° = 1.
What are the 12 trig functions?
The list of trigonometric identities shows more relations between these functions.crd(θ) = 2 sin( θ/2)versin(θ) = 1 − cos(θ) = 2 sin2( θ/2)coversin(θ) = 1 − sin(θ) = versin( π/2 − θ)haversin(θ) = 1/2versin(θ) = sin2( θ/2)exsec(θ) = sec(θ) − 1.excsc(θ) = exsec( π/2 − θ) = csc(θ) − 1.
What is SOH CAH TOA?
"SOHCAHTOA" is a helpful mnemonic for remembering the definitions of the trigonometric functions sine, cosine, and tangent i.e., sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, and tangent equals opposite over adjacent, (1) (2)
What is sin theta?
As per the sin theta formula, sin of an angle θ, in a right-angled triangle is equal to the ratio of opposite side and hypotenuse. The sine function is one of the important trigonometric functions apart from cos and tan.
What's the full meaning of sin?
an offense against religiousDefinition of sin (Entry 1 of 4) 1a : an offense against religious or moral law.
What is value of sin pi 4?
1/√2What is Sin pi/4? Sin pi/4 is the value of sine trigonometric function for an angle equal to pi/4 radians. The value of sin pi/4 is 1/√2 or 0.7071 (approx).
What is the value of sin pi by 2?
1Sin pi/2 is the value of sine trigonometric function for an angle equal to pi/2 radians. The value of sin pi/2 is 1.
What is value of Cos pi?
The value of cos pi =Cos 180° = cos(180° – 0°) = – cos 0° = – (1) = – 1. Hence, the value of cos pi = -1.
What do you Mean by Trigonometry?
Trigonometry is one of the branches of mathematics which deals with the relationship between the sides of a triangle (right triangle) with its angl...
What are the six basic Trigonometric Functions?
There are 6 trigonometric functions which are: Sine function Cosine function Tan function Sec function Cot function Cosec function
What is the formula for six trigonometry functions?
The formula for six trigonometry functions are: Sine A = Opposite side/Hypotenuse Cos A = Adjacent side / Hypotenuse Tan A = Opposite side / Adj...
What is the primary function of trigonometry?
The three primary functions of trigonometry are Sine function, Cosine function and Tangent Function.
Who is the founder of trigonometry?
A greek astronomer, geographer and mathematician, Hipparchus discovered the concept of trigonometry.
What are the Applications of Trigonometry in Real Life?
One of the most important real-life applications of trigonometry is in the calculation of height and distance. Some of the sectors where the concep...
1. How trigonometry is useful in everyday life?
Trigonometry plays a crucial role in several fields like navigation, construction, astrology, and satellites. Trigonometry has much importance in t...
2. Explain the different formulas that are used in trigonometry?
Several formulas are used in trigonometry that is crucial from the exam point of view.These six ratios are the most fundamental formulas which are...
3. What are the simple trigonometric ratios?
Sine, Cosine, Tangent, Cotangent, Secant and Cosecant.
4. What are formulas for trigonometry ratios?
Sin A = Perpendicular/HypotenuseCos A = Base/HypotenuseTan A = Perpendicular/Base
5. What are the 3 main features of trigonometry?
Sin, Cos and Tan are 3 major capabilities in trigonometry.
6. What are the fundamental trigonometric identities?
The 3 essential identities are:sin2 A + cos2 A = 11+tan2 A = sec2 A1+cot2 A = csc2 A
7. Trigonometry Formulas are applicable to which triangle?
They are applicable to proper-angled triangles.
Where does trigonometry come from?
The word trigonometry comes from the Greek words trigonon (“triangle”) and metron (“to measure”). Until about the 16th century, trigonometry was chiefly concerned with computing the numerical values of the missing parts of a triangle (or any shape that can be dissected into triangles) when the values of other parts were given. For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated. Such calculations distinguish trigonometry from geometry, which mainly investigates qualitative relations. Of course, this distinction is not always absolute: the Pythagorean theorem, for example, is a statement about the lengths of the three sides in a right triangle and is thus quantitative in nature. Still, in its original form, trigonometry was by and large an offspring of geometry; it was not until the 16th century that the two became separate branches of mathematics.
Who was the first person to use trigonometry?
See all videos for this article. The first major ancient work on trigonometry to reach Europe intact after the Dark Ages was the Almagest by Ptolemy ( c. 100–170 ce ). He lived in Alexandria, the intellectual centre of the Hellenistic world, but little else is known about him.
How many trigonometric functions are there in a right triangle?
These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly.
What is a triangle inscribed in a circle?
He considered every triangle—planar or spherical—as being inscribed in a circle, so that each side becomes a chord (that is, a straight line that connects two points on a curve or surface, as shown by the inscribed triangle ABC in the figure).
What was Hipparchus' main interest in trigonometry?
This became the chief task of trigonometry for the next several centuries. As an astronomer, Hipparchus was mainly interested in spherical triangles, such as the imaginary triangle formed by three stars on the celestial sphere, but he was also familiar with the basic formulas of plane trigonometry.
What are the functions of an angle?
trigonometry, the branch of mathematics concerned with specific functions of angles and their application to calculations. There are six functions of an angle commonly used in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly. These functions are properties of the angle A independent of the size of the triangle, and calculated values were tabulated for many angles before computers made trigonometry tables obsolete. Trigonometric functions are used in obtaining unknown angles and distances from known or measured angles in geometric figures.
What is the periodic function of a trigonometric function?
Trigonometric functions are periodic functions. A periodic function is a function , f, in which some positive value, p, exists such that. f (x+p) = f (x) for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f.
How to determine the value of a trigonometric function in any other quadrant?
Once we determine the reference angle, we can determine the value of the trigonometric functions in any of the other quadrants by applying the appropriate sign to their value for the reference angle.
What are the reciprocals of cosine and tangent?
Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively. As such, as long as we remember the definitions of sine, cosine, and tangent, we can take their reciprocals to determine the definitions of cosecant, secant, and cotangent.
What are the most common trigonometric functions?
Sine, cosine, and tangent are the most widely used trigonometric functions. Their reciprocals, though used, are less common in modern mathematics. Trigonometric functions are also called circular functions. There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. ...
What is the period of a cosine?
The sine, cosine, cosecant, and secant functions have a period of 2π. The tangent and cotangent functions have a period of π.
What are the two ways trigonometric functions are discussed?
There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. The right-angled triangle definition of trigonometric functions is most often how they are introduced, followed by their definitions in terms of the unit circle.
How many trigonometric functions are there in each quadrant?
Below is a table showing the signs of the 6 trigonometric functions in each quadrant.
What is trigonometry in math?
Trigonometry is of Latin origin and comes from the word triganon, which means triangle, and metron. The very meaning of trigonometry is to measure triangles. This type of mathematical function isn’t applied only to solving problems theoretically. Originally, trigonometry was the critical component in the navigation n oceans where no landmarks were ...
Why is trigonometry important?
During the calculation of the ocean's depth, size of the several marine creatures, the impact of sunlight on algal growth up to which middle of the sea can be known. Trigonometric formulas used in navigation compasses that are used by the sailor in the ocean.
What is the ratio between the hypotenuse in a right triangle to the side opposite an acute angle?
Cosecant is the ratio between the hypotenuse in a right triangle to the side opposite an acute angle.
How many ratios are there in trigonometric functions?
These six ratios are the most fundamental formulas which are contemplated to find the trigonometric elements. By using a right-angled triangle as the first reference, the trigonometric functions or identities are derived as the following:
What is sin in a triangle?
Sine is equivalent to the side opposite a given angle in a right triangle to the hypotenuse.
What happens when you divide a plane into 4 quadrants?
If we divide a plane into four quadrants, then all the trigonometric functions are positive in the first quadrant. In the third quadrant tan and cot is positive. In the 4th quadrant cos and sec positive. All the trigonometric identities are cyclic and repeat themselves. After the periodicity constant, the trigonometric identities repeat themselves. This periodicity constant varies from one trigonometric identity to another.
What is the opposite side of a right angle triangle?
Let us take a right-angle triangle to understand some formula. In right-angle triangle h is the Hypotenuse, p is the opposite side, b is the adjunct side.
What is the r of a trigonometric function?
To define trigonometric functions for any angle A, the angle is placed in position on a rectangular coordinate system with the vertex of A at the origin and the initial side of A along the positive x -axis; r (positive) is the distance from V to any point Q on the terminal side of A, and ( x, y) are the rectangular coordinates of Q.
Why are trigonometric tables useful?
Before computers rendered them obsolete in the late 20th century, such trigonometry tables were helpful to astronomers, surveyors, and engineers. For angles that are not integral multiples of the unit, the values of the functions may be interpolated.
Why are tangent and secant not defined?
Because division by zero is not allowed, the tangent and secant are not defined for angles the terminal side of which falls on the y -axis, and the cotangent and cosecant are undefined for angles the terminal side of which falls on the x -axis.
How many decimal places are there in a trigonometric function?
For most purposes, four or five decimal places are sufficient, and tables of this accuracy are common. Simple geometrical facts alone, however, suffice to determine the values of the trigonometric functions for the angles 0°, 30°, 45°, 60°, and 90°.
What is equal angles?
Equal angles are angles with the same measure; i.e., they have the same sign and the same number of degrees. Any angle − A has the same number of degrees as A but is of opposite sign. Its measure, therefore, is the negative of the measure of A. If two angles, A and B, have the initial sides VP and VQ and the terminal sides VQ and VR, respectively, then the angle A + B has the initial and terminal sides VP and VR. The angle A + B is called the sum of the angles A and B, and its relation to A and B when A is positive and B is positive or negative is illustrated in the figure. The sum A + B is the angle the measure of which is the algebraic sum of the measures of A and B. The difference A − B is the sum of A and − B. Thus, all angles coterminal with angle A (i.e., with the same initial and terminal sides as angle A) are given by A ± 360 n, in which 360 n is an angle of n complete revolutions. The angles (180 − A) and (90 − A) are the supplement and complement of angle A, respectively.
What are the units used to measure angles?
Numerical values can be assigned to angles by selecting a unit of measure. The most common units are the degree and the radian. There are 360° in a complete revolution, with each degree further divided into 60′ (minutes) and each minute divided into 60″ (seconds). In theoretical work, the radian is the most convenient unit.
When are angles considered positive?
Angles are considered positive when generated by counterclockwise rotations, negative when generated by clockwise rotations. The positive angle A and the negative angle A ′ in the figure are generated by less than one complete rotation of the line segment about the point V. All other positive and negative angles with the same initial ...
What is trigonometry formula?
Trigonometry Formulas: Trigonometry is the branch of mathematics that deals with the relationship between the sides and angles of a triangle. There are many interesting applications of Trigonometry that one can try out in their day-to-day lives. For example, if you are on the terrace of a tall building of known height and you see a post box on the other side of the road, you can easily calculate the width of the road using trigonometry formulas.
What class do you need to know about trigonometry?
Students are usually introduced to the basics of Trigonometry in high school (Class 9 or Class 10).
What is a trigonometric table?
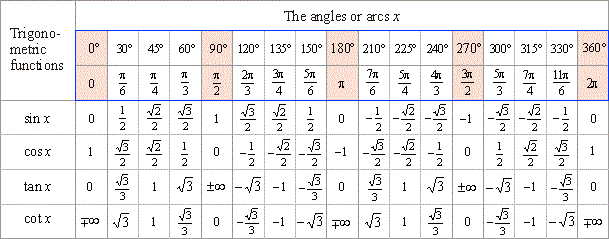
Trigonometry table is a table that you can refer to for the values of trigonometric ratios of different angles. Below is the table for trigonometry formulas of different angles which are commonly used for solving various problems.
What are the six trigonometric functions?
The six essential trigonometric functions are Sine, cosine, Secant, cosecant, tangent, and cotangent. The trigonometric functions and identities are derived by using the right-angled triangle. When the height and the base side of the right triangle are known, we can find out the sine, cosine, tangent, Secant, cosecant, and cotangent values using trigonometric formulas.
What are the reciprocals of the trigonometric ratios sine, cosine, and tangent?
Cosecant, Secant, and cotangent are the reciprocals of the basic trigonometric ratios sine, cosine, and tangent. All of these common identities are also are taken from the right-angled triangle. The reciprocal trigonometric identities are taken by using the trigonometric functions. They are utilised frequently to simplify trigonometric problems.
What is periodicity formula?
Periodicity formulas or identities are utilised to shift the angles by π 2, π , and 2π The periodicity identities are also termed the co-function identities. All the trigonometric identities are cyclic, which means they repeat themselves after a period. The period differs for various trigonometric identities.
What are the laws of the triangle?
Sine laws: The sine law and the cosine law give us the relationship between the sides and the angles of a triangle. The Sine Law gives the ratio of the sides and the angle opposite to the side.
What is the essential problem in trigonometry?
Plane trigonometry. In many applications of trigonometry the essential problem is the solution of triangles. If enough sides and angles are known, the remaining sides and angles as well as the area can be calculated, and the triangle is then said to be solved.
What are trigonometric functions?
Trigonometric functions of a real variable x are defined by means of the trigonometric functions of an angle. For example, sin x in which x is a real number is defined to have the value of the sine of the angle containing x radians. Similar definitions are made for the other five trigonometric functions of the real variable x. These functions satisfy the previously noted trigonometric relations with A, B, 90°, and 360° replaced by x, y, π/2 radians, and 2π radians, respectively. The minimum period of tan x and cot x is π, and of the other four functions it is 2π.
How are laws of sines and cosines expressed?
The law of sines is expressed as an equality involving three sine functions while the law of cosines is an identification of the cosine with an algebraic expression formed from the lengths of sides opposite the corresponding angles. To solve a triangle, all the known values are substituted into equations expressing the laws of sines and cosines, and the equations are solved for the unknown quantities. For example, the law of sines is employed when two angles and a side are known or when two sides and an angle opposite one are known. Similarly, the law of cosines is appropriate when two sides and an included angle are known or three sides are known.
What is the sum of the angles of a spherical triangle?
The sum of the angles of a spherical triangle is always greater than the sum of the angles in a planar triangle (π radians, equivalent to two right angles). The amount by which each spherical triangle exceeds two right angles (in radians) is known as its spherical excess. The area of a spherical triangle is given by the product ...
Why were spherical triangles studied?
Spherical triangles were subject to intense study from antiquity because of their usefulness in navigation, cartography, and astronomy. ( See above Passage to Europe .) The angles of a spherical triangle are defined by the angle of intersection of the corresponding tangent lines to each vertex. The sum of the angles of a spherical triangle is ...
How often do cosine and sine repeat?
Note that each of these functions is periodic. Thus, the sine and cosine functions repeat every 2π, and the tangent and cotangent functions repeat every π.
When to use law of sines?
For example, the law of sines is employed when two angles and a side are known or when two sides and an angle opposite one are known. Similarly, the law of cosines is appropriate when two sides and an included angle are known or three sides are known. Texts on trigonometry derive other formulas for solving triangles and for checking the solution.
Six Trigonometric Functions
The angles of sine, cosine, and tangent are the primary classification of functions of trigonometry. And the three functions which are cotangent, secant and cosecant can be derived from the primary functions. Basically, the other three functions are often used as compared to the primary trigonometric functions.
Formulas
Let us discuss the formulas given in the table below for functions of trigonometric ratios (sine, cosine, tangent, cotangent, secant and cosecant) for a right-angled triangle.
Table
The trigonometric ratio table for six functions like Sin, Cos, Tan, Cosec, Sec, Cot, are:
Graphs
By now we have known the formulas and values for different angles for all the trigonometric functions. Let us see here the graphs of all the six trigonometric functions to understand the alteration with respect to a time interval.
Frequently Asked Questions on Trigonometric Functions
The six trigonometric functions are Sine, Cosine, Tangent, Secant, Cosecant and Cotangent.
What is trigonometry?
Trigonometry is a branch of mathematics. The word itself comes from the Greek trigōnon (which means "triangle") and metron ("measure"). As the name suggests, trigonometry deals mostly with angles and triangles; in particular, it's defining and using the relationships and ratios between angles and sides in triangles. The primary application is thus solving triangles, specifically right triangles, but also any other type of triangle you like.
How to find trigonometric functions?
To find the trigonometric functions of an angle, enter the chosen angle in degrees or radians. Underneath the calculator, six most popular trig functions will appear - three basic ones: sine, cosine and tangent, and their reciprocals: cosecant, secant and cotangent. Additionally, if the angle is acute, the right triangle will be displayed, ...
How to find the height of a triangle?
You will have split the triangle into two smaller triangles. Solve either of these remaining triangles using regular trigonometry to find the height. Either the opposite or adjacent will now be the hypotenuse of the smaller triangle. Check your answers with Omni Calculator.
What is the relationship between two triangles?
one side and one angle. two sides. area and one side. Remember that if you know two angles, it's not enough to find the sides of the triangle. Two triangles having the same shape (which means they have equal angles) may be of different sizes (not the same side length) - that kind of relationship is called triangle similarity.
What is the study of the relationships within a triangle?
Trigonometry is the study of the relationships within a triangle. For right angled triangles, the ratio between any two sides is always the same, and are given as the trigonometry ratios, cos, sin, and tan. Trigonometry can also help find some missing triangular information, e.g., the sine rule.
What is the primary application of trigonometry?
The primary application is thus solving triangles, specifically right triangles, but also any other type of triangle you like. Trigonometry has plenty of applications: from everyday life problems such as calculating the height or distance between objects to the satellite navigation system, astronomy, and geography.
What are the two laws of trigonometry?
There are many other tools useful when dealing with trigonometry problems. Check out two popular trigonometric laws: law of sines and law of cosines calculators , helping to solve any kind of a triangle. If you want to read more about the trigonometric functions, go to our dedicated tools:
What is Trigonometry and How Do I Use It?
Trigonometry studies the relationships between the sides and angles of right triangles. The ratios between the measures of the sides of a right triangle and the measures of its angles are consistent, no matter how large or small the triangle.
When are Sin, Cos, and Tan Positive or Negative?
Depending on where the triangle is positioned in two dimensional space, the sin, cos, and tan values will be negative or positive.
How to find cosine in a triangle?
Cosine is a function where the cosine (also called " c o s ") value of an angle theta ( Θ) can be found by using the ratio of the side of the triangle adjacent to the angle Θ (that is not the hypotenuse) over the hypotenuse of the triangle.
How to find the sine of an angle theta?
Sine is a function where the sine (also called "sin") value of an angle theta can be found by using the ratio of the side of the triangle opposite the angle theta over the hypotenuse of the triangle.
What are the three trigs in Act?
To make the most of your ACT math prep, remember these three trig concepts: SOH, CAH, TOA, how to manipulate your equations, and how to recognize your function graphs.
Why is cosine even?
Cosine is an "even" function because it is symmetrical about the y-axis. This means that for all values of x, f ( x) = f ( − x). For example, in the graph above, y = 0.7 both when x = 1 and when x = − 1. Sometimes all the question will ask is for you to identify if a graph is even or odd or if a graph is sin or cos.
What is the branch of math that deals with right triangles and the relationships between their sides and angles?
Trigonometry is the branch of math that deals with right triangles and the relationships between their sides and angles. (The word "trig" is related to the word "triangle," to help you remember.)
Right Triangle Definition
Unit Circle Definition
Trigonometric Function Values For The Special Angles
Reference Angle
Trigonometric Functions Are Periodic Functions
- A periodic function is a function, f, in which some positive value, p, exists such that f(x+p) = f(x) for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f. All 6 trigonometric functions are periodic functions. No matter what point we start at on the unit circle, if we travel ...
Trigonometric Functions Are Odd Or Even
Inverse Trigonometric Functions
Graphs of The Trigonometric Functions