What does the central limit theorem enable researchers to do?
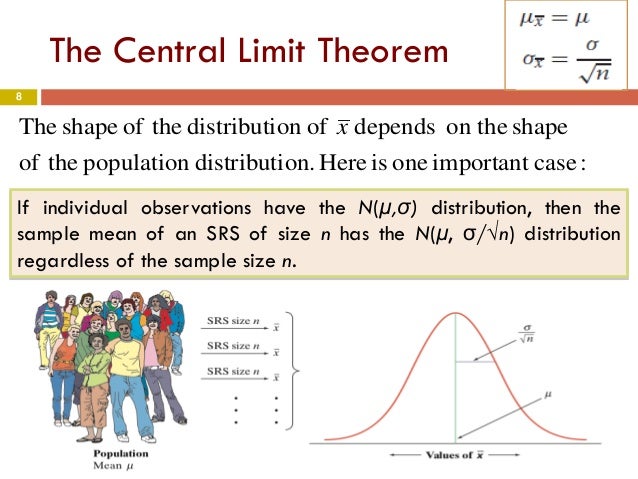
The central limit theorem tells us exactly what the shape of the distribution of means will be when we draw repeated samples from a given population. Specifically, as the sample sizes get larger, the distribution of means calculated from repeated sampling will approach normality.
How do you calculate the central limit theorem?
μ = E ( X i) = r = 3. while the variance of a chi-square random variable with three degrees of freedom is: σ 2 = V a r ( X i) = 2 r = 2 ( 3) = 6. The Central Limit Theorem, therefore, tells us that the sample mean X ¯ is approximately normally distributed with mean: μ X ¯ = μ = 3. and variance: σ X ¯ 2 = σ 2 n = 6 n.
What are the conditions for the central limit theorem?
The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed.
When can you use central limit theorem?
The central limit theorem can be used to illustrate the law of large numbers. The law of large numbers states that the larger the sample size you take from a population, the closer the sample mean gets to μ .
What is the central limit theorem and why is it important quizlet?
The central limit theorem tells us that if the sample is large (sample size of 30 or more), then the sampling distribution of the sample mean. Thus the correct answer is (a) if the sample size is reasonably large (for any population).
What is central limit theorem explain?
The Central Limit Theorem states that the sampling distribution of the sample means approaches a normal distribution as the sample size gets larger — no matter what the shape of the population distribution. This fact holds especially true for sample sizes over 30.
Why is the central limit theorem so important in quality control?
The central limit theorem also plays an important role in modern industrial quality control. The first step in improving the quality of a product is often to identify the major factors that contribute to unwanted variations. Efforts are then made to control these factors.
When can you apply central limit theorem?
If the sample size is at least 30 or the population is normally distributed, then the central limit theorem applies. If the sample size is less than 30 and the population is not normally distributed, then the central limit theorem does not apply.
How is central limit theorem used in real life?
Biologists use the central limit theorem whenever they use data from a sample of organisms to draw conclusions about the overall population of organisms. For example, a biologist may measure the height of 30 randomly selected plants and then use the sample mean height to estimate the population mean height.
What is central limit theorem PPT?
The Central Limit Theorem predicts that regardless of the distribution of the parent population: [1] The mean of the population of means is always equal to the mean of the parent population from which the population samples were drawn. [
What are the three parts of the central limit theorem?
To wrap up, there are three different components of the central limit theorem: Successive sampling from a population. Increasing sample size. Population distribution....Understanding the central limit theoremµ is the population mean.σ is the population standard deviation.n is the sample size.
How is central limit theorem used in real life?
Biologists use the central limit theorem whenever they use data from a sample of organisms to draw conclusions about the overall population of organisms. For example, a biologist may measure the height of 30 randomly selected plants and then use the sample mean height to estimate the population mean height.
What is the central limit theorem?
The central limit theorem relies on the concept of a sampling distribution, which is the probability distribution of a statistic for a large number of samples taken from a population.
Central limit theorem formula
Fortunately, you don’t need to actually repeatedly sample a population to know the shape of the sampling distribution. The parameters of the sampling distribution of the mean are determined by the parameters of the population:
Sample size and the central limit theorem
The sample size ( n) is the number of observations drawn from the population for each sample. The sample size is the same for all samples.
Conditions of the central limit theorem
The central limit theorem states that the sampling distribution of the mean will always follow a normal distribution under the following conditions:
Importance of the central limit theorem
The central limit theorem is one of the most fundamental statistical theorems. In fact, the “central” in “central limit theorem” refers to the importance of the theorem.
Central limit theorem examples
Applying the central limit theorem to real distributions may help you to better understand how it works.
What is the central limit theorem?
The Central Limit Theorem (CLT) is a mainstay of statistics and probability. The theorem expresses that as the size of the sample expands, the distribution of the mean among multiple samples will be like a Gaussian distribution.
What is the advantage of CLT?
The advantage of the CLT is that it is powerful , meaning implying that regardless of whether the data originates from an assortment of distributions if their mean and variance are the equivalent, the theorem can even now be utilized. The CLT notes that the sample means converge on the population means and the distance between them converges ...
What does LLN mean in CLT?
LLN expresses that the sample means of independent and indistinguishably distributed observations perceptions joins to a certain value as far as possible CLT portrays the distribution of the distinction between the sample means and the value.
How does CLT work?
The CLT works from the center out. That implies on the off chance that you are presuming close to the center, for example, that around two-thirds of future totals will fall inside one standard deviation of the mean, you can be secure even with little samples.
What is the CLT in statistics?
The CLT performs a significant part in statistical inference. It depicts precisely how much an increase in sample size diminishes sampling error, which tells us about the precision or margin of error for estimates of statistics, for example, percentages, from samples.
Which CLT loosens up the autonomy?
There are additional CLT that loosens up the autonomy or indistinguishably distributed conditions. For example, there is the Lindberg-Feller theorem, which despite everything, necessitates that the random variables be independent, yet it loosens up the indistinguishably distributed condition.
Why is normal distribution important?
Scaling and moving invariant the parameters only need to be rescaled. It is also useful for the identification of changes and scaling in operation. Many comparisons of many mean shift populations are conveniently checked by means of an analysis of the variance of the normal model (which is resilient against deviations from normality, while variations invariance can have a substantial effect on the results obtained).

What Is The Central Limit Theorem?
Central Limit Theorem Formula
- Fortunately, you don’t need to actually repeatedly sample a population to know the shape of the sampling distribution. The parametersof the sampling distribution of the mean are determined by the parameters of the population: 1. The meanof the sampling distribution is the mean of the population. 1. The standard deviationof the sampling distribution is the standard deviation of th…
Sample Size and The Central Limit Theorem
- The sample size (n) is the number of observations drawn from the population for each sample. The sample size is the same for all samples. The sample size affects the sampling distribution of the mean in two ways.
Conditions of The Central Limit Theorem
- The central limit theorem states that the sampling distribution of the mean will always follow a normal distributionunder the following conditions: 1. The sample size is sufficiently large. This condition is usually met if the sample size is n ≥ 30. 1. The samples are independent and identically distributed (i.i.d.) random variables. This condition...
Importance of The Central Limit Theorem
- The central limit theorem is one of the most fundamental statistical theorems. In fact, the “central” in “central limit theorem” refers to the importance of the theorem. The implication of the central limit theorem is that statistical theories that apply to normal distributions.
Central Limit Theorem Examples
- Applying the central limit theorem to real distributions may help you to better understand how it works.