The angle bisector
Bisection
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector (a line that passes through the midpoint of a given segment) and the angle bisector (a lin…
Which is the best definition for angle bisector?
An angle bisector is defined as a ray, segment, or line that divides a given angle into two angles of equal measures. The word bisector or bisection means dividing one thing into two equal parts. In geometry, we usually divide a triangle and an angle by a line or ray which is considered as an angle bisector.
What is the definition of bisector in geometry?
Definition of bisector : one that bisects especially : a straight line that bisects an angle or a line segment.
What is an angle bisector in a triangle?
The definition of the angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangle. In general, an angle bisector is equidistant from the sides of the angle when measured along a segment perpendicular to the sides of the angle.
What is the definition of angle bisector Brainly?
An angle bisector is a line or ray that divides an angle into two congruent angles.
What is the definition of angle in geometry?
What is Angle? An angle is formed when two straight lines or rays meet at a common endpoint. The common point of contact is called the vertex of an angle. The word angle comes from a Latin word named 'angulus,' meaning “corner.”
How do you find angle bisector?
An angle bisector divides an angle into two equal parts. So, to find where the angle bisector lays, divide the number of degrees in the angle by 2.
How do you find the angle bisector of a triangle?
0:513:59Angle Bisectors in a Triangle | Don't Memorise - YouTubeYouTubeStart of suggested clipEnd of suggested clipLet ray ad be the angle bisector of angle a which would make the measure of these two angles. EqualMoreLet ray ad be the angle bisector of angle a which would make the measure of these two angles. Equal let ray be e be the angle bisector of angle B. These two angles formed would be equal.
Which is true about angle bisector?
Angle BisectorBisectorIn geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector.https://en.wikipedia.org › wiki › BisectionBisection - Wikipedia Theorem: If a point is on the bisector of an angle, then the point is equidistant from the sides of the angle.
What is an example of definition of bisect?
Geometry. to cut or divide into two equal parts: to bisect an angle. to intersect or cross: the spot where the railroad tracks bisect the highway. verb (used without object) to split into two, as a road; fork: There's a charming old inn just before the road bisects.
How do you draw a bisector?
0:321:53How to draw the angle bisector of any angle - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo first we set our compass. To whatever radius we like and setting our compass on point V we scribeMoreSo first we set our compass. To whatever radius we like and setting our compass on point V we scribe an arc until it cuts both lines at two points which we will call B. And C as shown here.
How do you determine if a point is a bisector?
If a point is equidistant from the endpoints of a segment, then the point is on the perpendicular bisector of the segment.
Does a bisector cut an angle in half?
A bisectorbisectorIn geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector.https://en.wikipedia.org › wiki › BisectionBisection - Wikipedia cuts something in half. An angle bisector is a line which cuts a given angle in half. The perpendicular bisector of a line segment is the line which cuts the given segment in half and is at right angles to it.
What is an Angle Bisector?
An angle bisector or the bisector of an angle is a ray that divides an angle into two equal parts. For example, if a ray AX divides an angle of 60 degrees into two equal parts, then each measure will be equal to 30 degrees.
What is the bisector of an angle?
Every angle has an angle bisector. It is also the line of symmetry between the two arms of an angle, the construction of which enables you to construct smaller angles. Say you are required to construct a 30° angle. This can be performed by creating a 60° angle and then bisecting it. Similarly, 90-degree, 45-degree, 15-degree and other angles are constructed using the concept of an angle bisector.
How many parts does an angle bisector divide?
As we know, the angle bisector divides the angle into equal two parts.
How to construct an angle bisector?
Given a known or unknown ∠PQR, the steps to construct its angle bisector are: Step 1: Place the compass pointer at Q and make an arc that cuts the two arms of the angle at two different points. Step 2: From the point where the first arc cut the arm QP, make another arc towards the interior of the angle. Step 3: Without changing the radius on the ...
What is the degree of an angle?
Depending on the inclination between the two arms, an angle may be acute (less than 90-degrees, like 60-degree angle), obtuse (more than 90-degrees) or right angle (exactly 90-degrees). Constructing angles is an important part of geometry as this knowledge is extended for construction of other geometric figures as well, primarily the triangles.
How to bisect an angle?
In geometry, it is possible to bisect an angle using only a compass and ruler. To do so, use the following steps: 1 Place the point of the compass on vertex, O, and draw an arc of a circle such that the arc intersects both sides of the angle at points D and E, as shown in the above figure. 2 Draw two separate arcs of equal radius using both points D and E as centers. Make sure the radius is long enough so the arcs of the two circles can intersect at point F. 3 Use a ruler to draw a straight ray from O to F. OF bisects the angle AOB.
What is the point at which the three interior angle bisectors intersect?
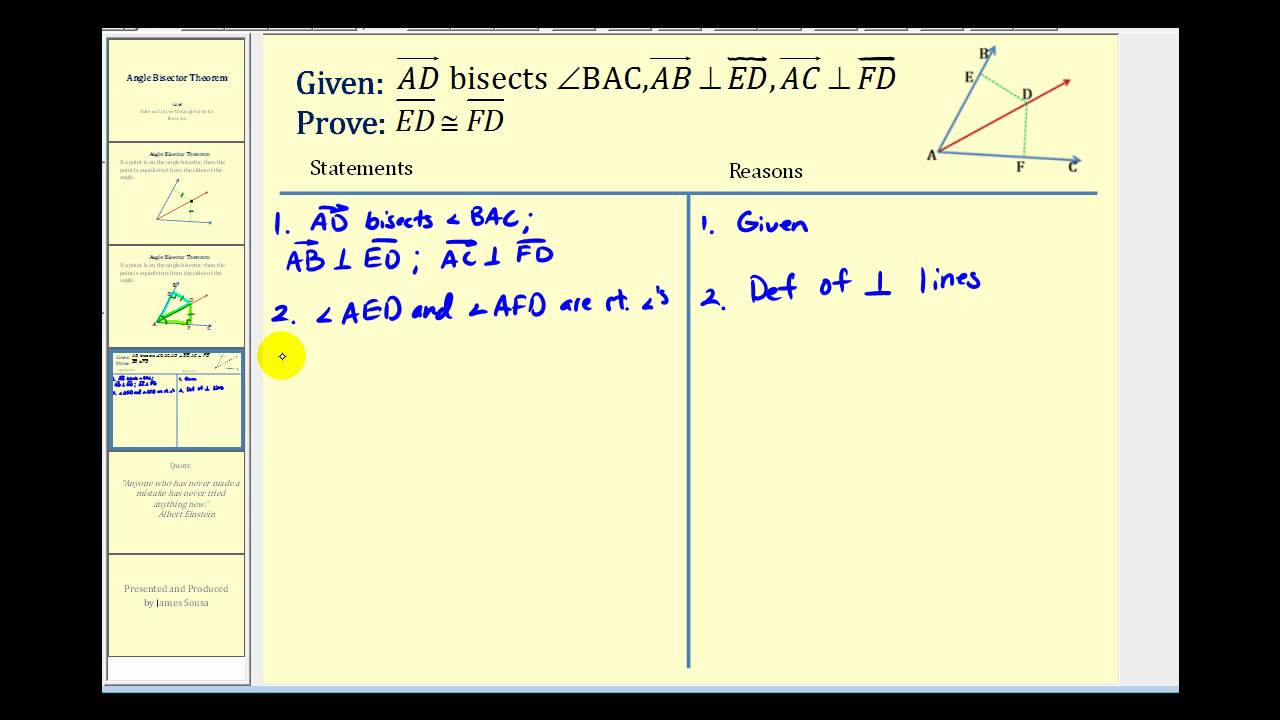
The point at which the three interior angle bisectors intersect is known as the incenter of the triangle. Referencing the diagram below, the three bisecting rays intersect at point D. Point D is the incenter of the triangle and is a point that is equidistant from the three sides of the triangle.
What is the equidistant theorem of angle bisectors?
If a point lies anywhere on an angle bisector, it is equidistant from the 2 sides of the bisected angle; this will be referred to as the equidistance theorem of angle bisectors, or equidistance theorem, for short.
What are the sides of an angle?
In the diagram above, the two sides of the angle are tangent to the circle and, DC and DA are the distances from the center of the circle to the sides. DC and DA are also the radii of the circle. Since all radii of a circle have equal measure, line BD bisects the angle.
When the two sides of an angle are tangent to a circle, what is the line segment or ray?
Based on the equidistance theorem, it can be seen that when the two sides that make up an angle are tangent to a circle, the line segment or ray formed by the angle's vertex and the circle's center is the angle's bisector.
Can you bisect an angle with a ruler?
In geometry, it is possible to bisect an angle using only a compass and ruler . To do so, use the following steps:
What is the angle bisector?
Angle Bisector Definition. The Angle Bisector Theorem helps you find unknown lengths of sides of triangles, because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangle's other two sides.
What is the bisector of a triangle?
An angle bisector of a triangle divides the interior angle's opposite side into two segments that are proportional to the other two sides of the triangle.
What is a linear object?
The linear object is an angle bisector. When it crossed side a a opposite ∠A ∠ A, it divided △ ABC △ A B C into two smaller triangles and divided side a a in two.
How many meters is BA B A?
Using cross multiplication ( 25 × 20 = 500 25 × 20 = 500) and then division ( 500 10 500 10) , we get BA B A = 50 meters.
What does the angle bisector theorem tell us?
The angle bisector theorem tells us what that way is. The angle bisector theorem tells us that the angle bisector divides the triangle's sides proportionally. When you have an angle bisector, you also have two smaller triangles.
What have we learned about the angle bisector theorem?
What have we learned? We've learned that the angle bisector theorem tells us the angle bisector divides a triangle into two proportional triangles whose sides are proportional. If we have a triangle ABC with angle bisector AD bisecting angle A, the proportion can be written in ratio form as BD/DC = AB/AC where BD, DC, AB, and AC are all line segments. We can use the angle bisector theorem and its ratio to help us check whether a line segment is an angle bisector or not and to help us find missing lengths.
How to find the missing length of side AB?
If we have a triangle ABC with angle bisector AD, we can find the missing length of side AB if we are given the lengths of sides BD, DC, and AC. We are given side BD = 5, DC = 10, and AC = 20. We can plug in these values into our ratio, and we will put an x for our side AB.
What is the bisector theorem?
Picture a triangle. Now picture one of the triangle's angles being split into two equal smaller triangles. That line that was used to cut the angle in half is called the angle bisector. When you do this to a triangle, it actually divides the triangle's sides in a unique way.
Is line AD an angle bisector?
The two sides are equal, and so yes, line AD is an angle bisector. Finding a Missing Side. Another way in which we can use the angle bisector theorem is when we need to find the length of a missing side. If we know the lengths of three of the sides mentioned in the angle bisector theorem ratio, we can find the length of the fourth side using ...
Is It an Angle Bisector?
Are the ratios equal to each other? If they are, then yes, the line segment is an angle bisector.

What Is An Angle bisector?
Properties of Angle Bisector
- All the points of angle bisector are equidistant from both the arms of the angle
- An angle bisector can be drawn to any angle, such as acute, obtuse, or right angle
- The angle bisector in a triangle divides the opposite side in a ratio that is equal to the ratio of the other two sides
How to Construct An Angle bisector?
- You require a ruler and a compass to construct angles and their bisectors. Given a known or unknown ∠PQR, the steps to construct its angle bisector are: Step 1:Place the compass pointer at Q and make an arc that cuts the two arms of the angle at two different points. Step 2:From the point where the first arc cut the arm QP, make another arc towards the interior of the angle. Ste…
Angle Bisector Theorem
- According to the angle bisector theorem, “an angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle”. Learn more: Angle Bisector Theorem
Related Articles
Solved Examples on Angle Bisector
- Q.1: If an angle bisector divides an angle of 80 degrees, then what is the measure of each angle? Solution: Given, a measure of an angle is 80 degrees As we know, the angle bisector divides the angle into equal two parts. Therefore, 80 degrees is divided into equal two parts, say x. Hence, x + x = 80° 2x = 80° x = 80°/2 x = 40° Q.2: A ray BX, divides an angle ABC into two equal parts. If one …
Practice Questions on Angle Bisector
- If an angle bisector divides 90 degrees, then what is the measure of each angle?
- Construct the angle bisector of 110 degrees angle.
- Construct an angle bisector of 30 degrees angle.
Table of Contents
Angle Bisector Definition
- The Angle Bisector Theoremhelps you find unknown lengths of sides of triangles, because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangle's other two sides.
How to Construct An Angle Bisector
- Draw △ABC△ABC on a piece of paper. Interior angles A,B,CA,B,C have opposite sides a,b,ca,b,c. Get some linear object and put one endpoint at ∠A∠A. Allow its other end to cross side aa. Divide ∠A∠A into two equal angles. You bisected ∠A∠A. The linear object is an angle bisector. When it crossed side aa opposite ∠A∠A, it divided △ABC△ABC into two smaller triangles and divided sid…
Angle Bisector Theorem
- Here is one version of the Angle Bisector Theorem: An angle bisector of a triangledivides the interior angle's opposite side into two segments that are proportional to the other two sides of the triangle. Angle bisector ADAD cuts side aa into two line segments, CDCD and DBDB. CDCD and DBDB relate to sides bb (CACA) and cc (BABA) in the same proportion as CACA and BABA relat…
Ratios & Proportions
- Ratios compare values. You can establish ratios between sides CACA and BABA, and line segments CDCD and DBDB. Proportionscompare ratios; you can learn if two ratios are equal. For △ABC△ABC with angle bisector ADAD, sides CACA and BABA, and side aa divided into CDCD and DBDB, we can set up ratios between the sides and line segments and compare them: CDDB=CA…
Angle Bisector Examples
- Suppose we are told a line segment ADAD divides side aa into CDCD and DBDB, of lengths 10 cm and 30 cm. We are also told side CACA is 30 cm and side BABAis 90 cm. See if the ratios are proportional to each other: CDDB=CABACDDB=CABA 1030=30901030=3090 We see 10301030 is the same ratio as 30903090, so ADADis an angle bisector.
Angle Bisector of A Triangle
- Using the Angle Bisector Theorem to Find An Unknown Side
If we know the length of original sides aa and bb, we can use the Angle Bisector Theorem to find the unknown length of side cc. The angle bisector divides side aa into CDCD and DBDB (the total length of side aa, CBCB). Assume these lengths: CD=10CD=10 DB=20DB=20 CA=25CA=25 Recal…
Lesson Summary
- You are now able to define the Angle Bisector Theorem, use ratios and proportions to verify an angle is a bisector, use the Angle Bisector Theorem to find the unknown lengths of sides of triangles, and identify an angle bisector by evaluating the lengths of the sides of the triangle.