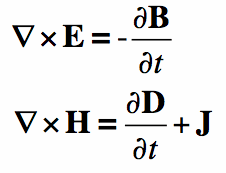
| Equation Name | Integral Equations Form |
| Gauss's Law for Static Electric Fields | Electric charge q produces an electric f ... |
| Gauss's Law for Static Magnetic Fields | The total magnetic flux passing through ... |
| Faraday's Law of Induction | Changing magnetic flux through a surface ... |
| Ampere's Law (with Maxwell's Addition of ... | An electric current I or a changing elec ... |
...
Constants.
| Magnetic constant | μ 0 = 4 π × 10 − 7 N A 2 ≈ 1.2566370614 . . . × 10 − 6 T ⋅ m A |
|---|---|
| Vacuum permittivity | ε 0 ≈ 8.854 187 817. . . × 10 − 12 F m (farads per meter) |
How to derive Maxwell equations?
- Using the BAC-CAB identity ∇ × ( ∇ × E) = ∇ ( ∇ ⋅ E) − ∇ 2 E {\displaystyle \nabla \times (\nabla \times \mathbf {E} )=\nabla (\nabla \cdot ...
- ∇ ( ∇ ⋅ E) − ∇ 2 E = − μ 0 ϵ 0 ∂ 2 E ∂ t 2 ∇ 2 E = μ 0 ϵ 0 ∂ ...
- The above equation is the wave equation in three dimensions.
What do Maxwell equations tell us?
The Maxwell equations tell us that electric charge never gets lost but is always conserved. In addition, they tell us how charged objects interact with each other. There are in total 4 Maxwell equations and each tells us something important about electricity, magnetism and their interplay.
Can we derive Maxwell equations from a more general theory?
We will derive the wave equation from Maxwell’s Equations in free space ... we can derive a second equation for the magnetic field: 22 2200 BB xt PH ww ww (4) Both equations (3) and (4) have the form of the general wave equation for a wave ( , )xt traveling in the x direction with speed v: 22 2 2 2 1 x v t ww\ ww.
How many Maxwell's equations are there?
Although there are just four today, Maxwell actually derived 20 equations in 1865. Later, Oliver Heaviside simplified them considerably. Using vector notation, he realised that 12 of the equations could be reduced to four - the four equations we see today. The remaining eight equations dealing with circuit analysis became a separate field of study.
What is the 4th Maxwell equation?
Can electric current flow through a capacitor?
Is equation 6 the final form?
About this website
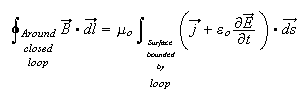
Is Ampere's law a Maxwell equation?
The fourth of Maxwell's law is Ampere's law. The Ampere's law states that the generation of magnetic fields can be done in two methods namely with electric current as well as with changing electric fields.
What is the expression for Ampere Maxwell law?
dl=mu_(0)i_(c)+epsi_(0)(dphi_E)/(dt)`.
What is the formula of Maxwell equation?
∫→E⋅d→A=q/ε0. This is Maxwell's first equation.
What are the 4 Maxwell's equations?
The four Maxwell equations, corresponding to the four statements above, are: (1) div D = ρ, (2) div B = 0, (3) curl E = -dB/dt, and (4) curl H = dD/dt + J. What force slows motion?
How many are Maxwell equations?
fourAlthough there are just four today, Maxwell actually derived 20 equations in 1865. Later, Oliver Heaviside simplified them considerably. Using vector notation, he realised that 12 of the equations could be reduced to four – the four equations we see today.
What is Ampere current law?
Ampere's Law can be stated as: “The magnetic field created by an electric current is proportional to the size of that electric current with a constant of proportionality equal to the permeability of free space.”
What is Maxwell equation in physics?
Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equation and the constitutive relations.
How does Maxwell fix Ampere's law?
Maxwell corrected the Ampere's circuital law by including displacement current. He said that there is not only the current existed outside the capacitor but also current known as displacement currentexisted between the plates of the capacitor.
What is Maxwell third equation?
by amsh. Statement. (a) It states that,whenever magnetic flux linked with a circuit changes then induced electromotive force (emf) is set up in the circuit. This induced emf lasts so long as the change in magnetic flux continues.
What is Maxwell second equation?
Equation (2) is the Differential form of Maxwell's first equation. Maxwell's second equation or Gauss's law for Magnetism. Statement. It states that the total magnetic flux φm emerging through a closed surface is zero. φm=∫B.dS=0 (3)
Ampere’s Law - Definition, Equations, Derivations & Applications
Ampere’s Law has a lot of implications in real life, however, some of the most popular applications include determining the Magnetic Induction due to the long current-carrying wire, determining the Magnetic field inside a toroid, determining the Magnetic field created by a long current carrying conducting cylinder, determining the Magnetic field inside the conductor.
Ampère's Law – The Physics Hypertextbook
the single loop of wire. Given a current carrying loop of wire with radius a, determine the magnetic field strength anywhere along its axis of rotation at any distance x away from its center.. Start with the Biot-Savart Law because the problem says to.
What is the Ampere Maxwell equation?
The Ampere-Maxwell equation relates electric currents and magnetic flux. It describes the magnetic fields that result from a transmitter wire or loop in electromagnetic surveys. For steady currents, it is key for describing the magnetometric resistivity experiment.
What is the total current in the Ampere-Maxwell equation?
The total current involved in the Ampere-Maxwell equation consists of free current and bound current, although all currents are essentially the same from a microscopic perspective. Treating free current and bound current differently offers physical insights to the Ampere-Maxwell equation in different contexts.
What is the relationship between magnetic field and current?
The first observation that spurred researchers to look for the relationship linking magnetic field and current was made by Hans Christian Ørsted in 1820, who noticed that magnetic needles were deflected by electric currents. This led several physicists in Europe to study this phenomenon in parallel. While Jean-Baptiste Biot and Félix Savart were experimenting with a setup similar to Ørsted’s experiment (that lead them to define in 1820 a relationship known now as the Biot-Savart’s law), André-Marie Ampère’s experiment focused on measuring the forces that two electric wires exert on each other. He formulated the Ampere’s circuital law in 1826 [Gri99], which relates the magnetic field associated with a closed loop to the electric current passing through it. In its original form, the current enclosed by the loop only refers to free current caused by moving charges, causing several issues regarding the conservation of electric charge and the propagation of electromagnetic energy.
What is the difference between bound charge due to magnetization and bound charge due to electric polarization?
Note that the bound charge due to magnetization is integrated into the magnetic field h, whereas the bound charge due to electric polarization is integrated into the displacement field d.
How is bound current induced?
In contrast, the bound current is induced by a magnetization or a polarization in bulk materials . When a magnetic material is placed in an external magnetic field, a magnetization current will be induced due to the motion of electrons in atoms.
What is the second portion of Maxwell's contribution?
The second portion of the equation is Maxwell’ s contribution and shows that a circulation of magnetic field is also caused by a time rate of change of electric flux. This explains how current in a simple circuit involving a battery and capacitor can flow. The term is pivotal in showing that electromagnetic energy propagates as waves.
What is the polarization of a dielectric?
j p = ∂ p ∂ t is the polarization or bound current, where p is the electric polarization resulting from bound charges in dielectrics
Why is Maxwell's addition to Ampère's law important?
Maxwell's addition to Ampère's law is particularly important: it makes the set of equations mathematically consistent for non static fields, without changing the laws of Ampere and Gauss for static fields. However, as a consequence, it predicts that a changing magnetic field induces an electric field and vice versa.
What are Maxwell's equations?
Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, ...
Why are Maxwell equations so scarce?
Popular variations on the Maxwell equations as a classical theory of electromagnetic fields are relatively scarce because the standard equations have stood the test of time remarkably well.
How many equations are there in the electric and magnetic field?
In the electric and magnetic field formulation there are four equations that determine the fields for given charge and current distribution. A separate law of nature, the Lorentz force law, describes how, conversely, the electric and magnetic fields act on charged particles and currents. A version of this law was included in the original equations by Maxwell but, by convention, is included no longer. The vector calculus formalism below, the work of Oliver Heaviside, has become standard. It is manifestly rotation invariant, and therefore mathematically much more transparent than Maxwell's original 20 equations in x,y,z components. The relativistic formulations are even more symmetric and manifestly Lorentz invariant. For the same equations expressed using tensor calculus or differential forms, see alternative formulations .
How to apply Maxwell's macroscopic equations?
In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field D and the electric field E, as well as the magnetizing field H and the magnetic field B. Equivalently, we have to specify the dependence of the polarization P (hence the bound charge) and the magnetization M (hence the bound current) on the applied electric and magnetic field. The equations specifying this response are called constitutive relations. For real-world materials, the constitutive relations are rarely simple, except approximately, and usually determined by experiment. See the main article on constitutive relations for a fuller description. : 44–45
What is the covariant formulation of Maxwell's equations?
The covariant formulation (on spacetime rather than space and time separately) makes the compatibility of Maxwell's equations with special relativity manifest. Maxwell's equations in curved spacetime, commonly used in high energy and gravitational physics, are compatible with general relativity.
How many unknowns are there in Maxwell's equations?
Maxwell's equations seem overdetermined, in that they involve six unknowns (the three components of E and B) but eight equations (one for each of the two Gauss's laws, three vector components each for Faraday's and Ampere's laws).
How many equations are there in Maxwell's equations?
Maxwell's Equations are composed of four equations with each one describes one phenomenon respectively.
What equations explain electromagnetic waves?
The combination of equations 3 and 4 can explain electromagnetic wave (such as light) which can propagate on its own. The combination says that a changing magnetic field produces a changing electric field, and this changing electric field produces another changing magnetic field. Thus the cycle continues and an electromagnetic wave is made ...
What induces a circulating electric field?
A changing magnetic field induces a circulating electric field.
What is the electric field flux passing through a closed surface?
The electric field flux passing through any closed surface is proportional to the total charge contained within that surface
How to calculate magnetic field circulation?
This magnetic field circulation is calculated by doing a line integral of the dot product of B and dl (an infinitely small differential length of the path) on the closed path C
How to calculate circulation?
Calculate the circulation by doing a line integral of A around path C. This line integral is done by always keeping the inside of the circle at the left side of the path.
Which law says a changing magnetic field (changing with time) produces an electric field?
Faraday's law which says a changing magnetic field (changing with time) produces an electric field. Ampere-Maxwell's law which says a changing electric field (changing with time) produces a magnetic field. The combination of equations 3 and 4 can explain electromagnetic wave (such as light) which can propagate on its own.
What is the second Maxwell equation?
The second Maxwell equation is analogous to Gauss’s law in Electrostatics. For the magnetic field, the field lines flow around in closed curves. Considering the force lines representing a kind of fluid flow, the so-called “magnetic flux”, we see that magnetic flux flows into the surface as much as it flows out for a closed surface. Therefore, the net magnetic flux out of the enclosed volume is zero. This formula is called Maxwell’s second equation.
What is the Displacement Current?
The type of current produced due to changes in the electric field is called the displacement current. It varies with time according to Maxwell’s equation The S.I. unit of displacement current is Ampere (Amp).
What is the phenomenon of induction of magnetic field due to change in the electric field?
The phenomenon of induction of the magnetic field due to change in the electric field is explained in electromagnetic theory . The magnetic field is produced in the surroundings of the electric current, and it is called conduction current. The concept of displacement current depends on the variation of the Electric field with time. It was developed by the British physicist James Clerk Maxwell in the 19 th century. Let’s discuss the displacement current formula and Maxwell’s equations in this article.
Who assumed that there must be some current between the capacitor plates during the charging process?
James Clerk Maxwell assumed that there must be some current between the capacitor plates during the charging process. He named it displacement current. Hence modified Ampere’s law is as follows:
Is the Amperian loop valid for constant currents?
4. This law is valid only for steady or constant currents. This law is valid irrespective of the size and shape of the closed path (Amperian loop) enclosing the current.
Is Kirchhoff's first law valid at each capacitor plate?
Kirchhoff’s first law is valid at each capacitor plate provided that we take the sum of conduction and displacement current.
What is the primary equation of Maxwell's law?
The primary equation permits you to determine the electric field formed with a charge. The next equation permits you to determine the magnetic field, and the remaining two will explain how fields flow around their supplies. This article discusses Maxwell theory or Maxwell’s law.
What are Maxwell's four equations?
Maxwell’s Four Equations. Maxwell’s four equations explain the two fields occurring from the supplies of electric as well as current. The fields are namely electric as well as magnetic, and how they vary within time. The four Maxwell’s equations include the following. The above four Maxwell’s equations are Gauss for electricity, ...
What is the first law of Maxwell's equation?
Maxwells Equations. The first law is Gauss law intended for static electric fields. The second law is also Gauss law intended for static magnetic fields. The third law is Faraday’s law that tells the change of magnetic field will produce an electric field. The fourth law is Ampere Maxwell’s law that tells the change of electric field will produce ...
What is Maxwell's law?
The Gauss law defines that the electric flux from any closed surface will be proportional toward the whole charge enclosed in the surface.
How many equations are there in Maxwell's equations?
The Maxwell Equation derivation is collected by four equations, where each equation explains one fact correspondingly. All these equations are not invented by Maxwell; however, he combined the four equations which are made by Faraday, Gauss, and Ampere. Although Maxwell included one part of information into the fourth equation namely Ampere’s law, that makes the equation complete.
What is Gauss' law integral form?
The Gauss’ law integral form discovers application during electric fields calculation in the region of charged objects. By applying this law to a point charge in the electric field, one can demonstrate that it is dependable with Coulomb’s law.
Does Maxwell's amperes law work for non-static fields?
The Maxwell’s amperes law will make the set of the equations accurately reliable for non-static fields without altering the Ampere as well as Gauss laws for fixed fields. But as a result, it expects that a change of the magnetic field will induce an electric field.
Introduction
To say that James Clerk Maxwell revolutionized the world of Electrodynamics would be an understatement. The four equations named after him stand as a testament to his contribution to the field.
Prerequisite
At the very least, the reader of this article must be comfortably acquainted with Ampere's law and the steady-state equations of electromagnetism. These include Gauss' law, Faraday's law, and the non-existence of magnetic monopoles, evidenced by the vanishing divergence of magnetic flux intensity, B.
Electromagnetism Before Maxwell
When Maxwell began his work over a century ago, our entire knowledge of electromagnetism was limited to the abovementioned equations. Perhaps due to limited resources or some other reason, a very obvious problem escaped our attention until Maxwell pointed it out.
A "Fatal Flaw"
This situation arises when you try to find the divergence of the quantities on either side of the fourth equation. It is a well-known and mathematically sound fact that the divergence of the curl of a vector field is, without any exclusion, zero.
A Little Bit of Exercise
In the image attached above, I have drawn a capacitor connected to an emf source, and two Amperian loops, labelled 1 and 2.
Fixing Ampere's Law
The equation of continuity can be used to relate current density with charge density, which is proportional to the divergence of time derivative of electric field via Gauss' law.
Displacement Current
This is the modified form of Ampere's law, with the additional term of µ 0 ε 0 (∂ E /∂t). Note that in steady conditions where E is a constant in time, the equation reverts back to its original form.
What is the 4th Maxwell equation?
The 4th Maxwell's Equation. Ampere was a scientist experimenting with forces on wires carrying electric current. He was doing these experiments back in the 1820s, about the same time that Farday was working on Faraday's Law. Ampere and Farday didn't know that there work would be unified by Maxwell himself, about 4 decades later.
Can electric current flow through a capacitor?
However, a capacitor is basically two parallel conductive plates separated by air. Hence, there is no conductive path for the current to flow through. This means that no electric current can flow through the air of the capacitor. This is a problem if we think about Equation [8].
Is equation 6 the final form?
If you are an astute learner, you may notice that Equation [6] is not the final form, which is written in Equation [1]. There is a problem with Equation [6], but it wasn't until the 1860s that James Clerk Maxwell figured out the problem, and unified electromagnetics with Maxwell's Equations.

The 4th Maxwell's Equation
- On this page, we'll explain the meaning of the last of Maxwell's Equations, Ampere's Law, which is given in Equation : Ampere was a scientist experimenting with forces on wires carrying electric current. He was doing these experiments back in the 1820s, about the same time that Farday was working on Faraday's Law. Ampere and Farday didn't know that...
Manipulating The Math For Ampere's Law
- We are going to do the same trick with Stoke's Theorem that we did when looking at Faraday's Law. We can rewrite Ampere's Law in Equation : On the right side equality in Equation , we have used Stokes' Theorem to change a line integral around a closed loop into the curl of the same field through the surface enclosed by the loop (S). We can also rewrite the total current () as the surfa…
Displacement Current Density
- Ampere's Law was written as in Equation up until Maxwell. So let's look at what is wrong with it. First, I have to throw out another vector identity - the divergence of the curlof any vector field is always zero: So let's take the divergence of Ampere's Law as written in Equation : So Equation follows from Equations and . But it says that the divergence of the current density Jis always zer…
Overview
Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They de…
Formulation in terms of electric and magnetic fields (microscopic or in vacuum version)
In the electric and magnetic field formulation there are four equations that determine the fields for given charge and current distribution. A separate law of nature, the Lorentz force law, describes how, conversely, the electric and magnetic fields act on charged particles and currents. A version of this law was included in the original equations by Maxwell but, by convention, is included no longer. The vector calculus formalism below, the work of Oliver Heaviside, has become standard. …
Conceptual descriptions
Gauss's law describes the relationship between a static electric field and electric charges: a static electric field points away from positive charges and towards negative charges, and the net outflow of the electric field through a closed surface is proportional to the enclosed charge, including bound charge due to polarization of material. The coefficient of the proportion is the permittivity of f…
Charge conservation
The invariance of charge can be derived as a corollary of Maxwell's equations. The left-hand side of the modified Ampere's Law has zero divergence by the div–curl identity. Expanding the divergence of the right-hand side, interchanging derivatives, and applying Gauss's law gives:
In particular, in an isolated system the total charge is conserved.
Vacuum equations, electromagnetic waves and speed of light
In a region with no charges (ρ = 0) and no currents (J = 0), such as in a vacuum, Maxwell's equations reduce to:
Taking the curl (∇×) of the curl equations, and using the curl of the curl identity we obtain
The quantity has the dimension of (time/length) . Defining , the equations above have the form of the standard wave equations
Macroscopic formulation
The above equations are the microscopic version of Maxwell's equations, expressing the electric and the magnetic fields in terms of the (possibly atomic-level) charges and currents present. This is sometimes called the "general" form, but the macroscopic version below is equally general, the difference being one of bookkeeping.
Relativistic formulations
The Maxwell equations can also be formulated on a spacetime-like Minkowski space where space and time are treated on equal footing. The direct spacetime formulations make manifest that the Maxwell equations are relativistically invariant. Because of this symmetry, the electric and magnetic fields are treated on equal footing and are recognised as components of the Faraday tensor. This reduces the four Maxwell equations to two, which simplifies the equations, althoug…
Solutions
Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equation and the constitutive relations. These all form a set of coupled partial differential equations which are often very difficult to solve: the solutions encompass all the diverse phenomena of classical electroma…