what is the meaning of symmetry in physics

Full Answer

What exactly do we mean by symmetry in physics?

symmetry, in physics, the concept that the properties of particles such as atoms and molecules remain unchanged after being subjected to a variety of symmetry transformations or “operations.”

What is the principle of symmetry?

What is symmetry? Symmetry is one of the Gestalt Principles. It is a visual property in which elements are made up of equivalent parts to resemble proportion and balance. A common example would be how human faces have two equivalent elements like eyes, ears, hands, and legs that create a balance forming symmetry. Symmetry in human faces.

Is physics the one true science?

Yes, physics is the basis of chemistry and chemistry is the basis of biology. Actually chemistry and biology are a very small part of complex physics. Physics is far beyond chemicals and life. Its the basis of the very existence of everything inside the universe. Hope it helped you.

How to differentiate in physics?

The basic differentiation rules that need to be followed are as follows:

• Sum and Difference Rule
• Product Rule
• Quotient Rule
• Chain Rule

What is symmetry explain with example?

Symmetry is defined as a proportionate and balanced similarity that is found in two halves of an object, that is, one-half is the mirror image of the other half. For example, different shapes like square, rectangle, circle are symmetric along their respective lines of symmetry.

How many symmetry are there in physics?

threeImportant symmetries in quantum physics. Generally, there are three important symmetries which essentially give rise to these conservation laws. Those are C-symmetry (charge), P-symmetry (parity, or more simply space) and T-symmetry (time).

What is the symmetric and asymmetric in physics?

Asymmetry is the absence of, or a violation of, symmetry (the property of an object being invariant to a transformation, such as reflection). Symmetry is an important property of both physical and abstract systems and it may be displayed in precise terms or in more aesthetic terms.

What are the 4 types of symmetry?

Types of symmetries are rotational symmetry, reflection symmetry, translation symmetry, and glide reflection symmetry. These four types of symmetries are examples of different types of symmetry on a flat surface called planar symmetry.

What is symmetry formula?

The axis of symmetry formula is given as, for a quadratic equation with standard form as y = ax2 + bx + c, is: x = -b/2a.

Why is symmetry in physics important?

A more important implication of symmetry in physics is the existence of conservation laws. For every global continuous symmetry—i.e., a transformation of a physical system that acts the same way everywhere and at all times—there exists an associated time independent quantity: a conserved charge.

What are the types of symmetry?

There are four types of symmetry that can be observed in various situations, they are:Translation Symmetry.Rotational Symmetry.Reflection Symmetry.Glide Symmetry.

What is the full meaning of symmetrical?

Definition of symmetrical 1 : having, involving, or exhibiting symmetry. 2 : having corresponding points whose connecting lines are bisected by a given point or perpendicularly bisected by a given line or plane symmetrical curves.

How many types of symmetry are there?

There are three types of symmetry: reflection (bilateral), rotational (radial), and translational symmetry.

How many symmetry are there?

But basically there are two types of lines of symmetry, they are: Vertical Line of Symmetry. Horizontal Line of Symmetry.

How many total symmetry are there?

Broadly, there exist two types of symmetry, namely translational symmetry and point symmetry.

How many symmetry is there?

There are four types of symmetry that can be observed in various situations, they are: Translation Symmetry. Rotational Symmetry. Reflection Symmetry.

What is symmetry in physics?

In physics, a symmetry of a physical system is a physical or mathematical feature of the system (observed or intrinsic) that is preserved or remains unchanged under some transformation . A family of particular transformations may be continuous (such as rotation of a circle) or discrete (e.g., reflection of a bilaterally symmetric figure, ...

Which symmetry is part of some theories of physics and not in others?

Another symmetry which is part of some theories of physics and not in others is scale invariance which involve Weyl transformations of the following kind:

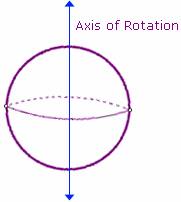
What are some examples of rotational symmetry?

The two examples of rotational symmetry described above – spherical and cylindrical – are each instances of continuous symmetry. These are characterised by invariance following a continuous change in the geometry of the system. For example, the wire may be rotated through any angle about its axis and the field strength will be the same on a given cylinder. Mathematically, continuous symmetries are described by transformations that change continuously as a function of their parameterization. An important subclass of continuous symmetries in physics are spacetime symmetries.

What is global symmetry?

A global symmetry is one that keeps a property invariant for a transformation that is applied simultaneously at all points of spacetime, whereas a local symmetry is one that keeps a property invariant when a possibly different symmetry transformation is applied at each point of spacetime; specifically a local symmetry transformation is parameterised by the spacetime co-ordinates, whereas a global symmetry is not. This implies that a global symmetry is also a local symmetry. Local symmetries play an important role in physics as they form the basis for gauge theories .

How do continuous symmetries preserve transformations?

Continuous symmetries in physics preserve transformations. One can specify a symmetry by showing how a very small transformation affects various particle fields. The commutator of two of these infinitesimal transformations are equivalent to a third infinitesimal transformation of the same kind hence they form a Lie algebra .

What are continuous symmetries?

Continuous symmetries can be described by Lie groups while discrete symmetries are described by finite groups ( see Symmetry group ). These two concepts, Lie and finite groups, are the foundation for the fundamental theories of modern physics. Symmetries are frequently amenable to mathematical formulations such as group representations and can, ...

How is symmetry related to conservation?

The symmetry properties of a physical system are intimately related to the conservation laws characterizing that system. Noether's theorem gives a precise description of this relation. The theorem states that each continuous symmetry of a physical system implies that some physical property of that system is conserved. Conversely, each conserved quantity has a corresponding symmetry. For example, spatial translation symmetry (i.e. homogeneity of space) gives rise to conservation of (linear) momentum, and temporal translation symmetry (i.e. homogeneity of time) gives rise to conservation of energy .

Why was the name "Symmetry" chosen?

But no, it was picked because symmetry is deeply central to particle physics (and many other areas of physics, which I’ll get to in a bit). To understand why let me start by explaining what a symmetry is.

What is the mathematical language used to talk about symmetry in physics?

The mathematical language used to talk about symmetry in physics is called group theory . Group theory is an area of mathematics which everyone with at least a Bachelor’s degree in mathematics is usually familiar with, but since it’s not taught in high school (despite the basics of it being no more difficult than high school math) or required of non-math majors, most people outside of math or physics professions have not heard of it.

How do particle physicists come up with their theories?

These correspond to the forces of nature known as the strong force, the weak force, and electromagnetism. When theoretical particle physicists come up with theories that go beyond the Standard Model, they do so by adding other ingredients in the form of additional symmetries. For example, in graduate school I worked on a grand unified theory proposed by my advisor called the Pentagon Model which was based on 3 copies of the symmetry group SU (5), where the smaller groups mentioned above resided inside one of the three copies.

What is symmetry magazine?

First, let me help convince you, if you’re not already, that symmetry is important and central in physics. One of the best online sources for news in the particle physics industry is Symmetry Magazine. This is a joint publication between SLAC and Fermilab, the 2 biggest particle accelerators in the US. It’s funded by the Department of Energy. Due to a decision by US politicians in the 1990’s to abandon building a bigger accelerator, in recent years CERN in Europe has now stolen the spotlight from these US accelerators; but the magazine is still widely read even by physicists living and working outside the US. The particle physicists at SLAC and Fermilab could have chosen any name for a magazine describing their industry. It could have been called Particle Magazine, Quantum Magazine, Subatomic Physics Magazine or many other things indicative of particle physics. But in fact it’s called Symmetry Magazine. Why?

What is the symmetry of snowflakes?

This is a form of rotational symmetry. With perfect continuous rotational symmetry, you would be able to rotate an image in a plane around a center point in that plane by any angle and the image should remain the same. However, the only images that have this continuous rotational symmetry are concentric rings of different colors/material —by comparison pretty boring. Snowflakes and mandalas have a more interesting discrete rotational symmetry associated with rotations by a fixed angle, some fraction of the whole 360 degree circle. Every time you rotate by this fixed angle, you get back to the original image. If there are imperfections (as there often are in snowflakes) in some sectors of the circle and not others, then this symmetry is broken but as long as it is still mostly symmetric we could still call it an “approximate symmetry”. Slightly broken symmetries are very important for physics. I’ll explain why later.

Which is more fundamental, cosmology or particle physics?

Particle physics and cosmology are the two areas of physics generally considered the most “fundamental” (in the same sense that physics is considered more fundamental than chemistry or biology). The other areas of physics deal with emergent phenomena which are thought — at least in principle — to ultimately reduce down to either particle physics or cosmology. But is symmetry also important for those more emergent/practical branches of physics? I don’t think it plays quite as central a role there, but yes it is still very important for these emergent areas.

Is supersymmetry still theoretical?

I also worked quite a bit on a symmetry known as supersymmetry, which is still theoretical but if found would solve/explain several of the most important outstanding unsolved problems in particle physics today. When the LHC ( Large Hadron Collider) at CERN was built, the argument for building it was based on the potential for discovering new physics which was motivated by a number of independent arguments. The strongest argument presented to those responsible for funding the construction of the collider was that we would be very likely to find the Higgs boson. The second strongest argument was that we would have a good chance of finding supersymmetry particles. The Higgs boson has subsequently been found, so that argument proved to be valid. We still haven’t found supersymmetry, but there are still many in the particle physics community who think we might soon, and many more who think that even if we don’t it may exist at energies which LHC cannot reach. (Incidentally, the logo for this blog displays the mathematical equations — called anti-commutation relations — which define supersymmetry.)

What does symmetry mean in physics?

This also applies to physics in a similar way. In physics, a symmetry is generalised to esentially mean an invariance in a quantity, under any sort of transformation.

What is symmetry in math?

To be more formal, in mathematics, a symmetry can be defined as the quality of being invariant under a transformation. A transformation in this case can be any sort of mathematical operation that we can apply to a system (or figure). This can be anything like reflection, rotation or scaling. In Physics...

What is transformation in quantum theory?

In the quantum world, we can consider a transformation to be an interaction of one or more particles through one of the fundamental forces described above . For example... An interaction could be, for instance, an electron absorbing a photon of a certain energy, raising the electron's energy level.

Why is a circle symmetric?

A circle is symmetric about an infinite number of axes, because you can draw any line that goes through the circle's centre and it would be symmetric about it. And since we can draw an infinite number of lines through a circle's centre, it must have an infinite number of axes of symmetry.

What are the three symmetries of quantum physics?

Generally, there are three important symmetries which essentially give rise to these conservation laws. Those are C-symmetry (charge), P-symmetry (parity, or more simply space) and T-symmetry (time).

What is conservation in physics?

A conservation in a quantity implies invariance , which means the total amount of a quantity in a system does not change. Essentially, when we talk about a symmetry in physics, we are talking about a conservation law such as the law of conservation of energy . Example: conservation of energy.

Is symmetry a conservation law?

Now, remember also from the above that a symmetry is essentially a conservation law in physics. At least, a result of a symmetry is a conservation law. That is, every symmetry corresponds to a conservation law (this is known more formally as Noether's theorem ).

What is symmetry in math?

The definition of symmetry as “invariance under a specified group of transformations” allowed the concept to be applied much more widely, not only to spatial figures but also to abstract objects such as mathematical expressions — in particular, expressions of physical relevance such as dynamical equations.

Where does the term "symmetry" come from?

The Concept of Symmetry. The term “symmetry” derives from the Greek words sun (meaning ‘with’ or ‘together’) and metron (‘measure’), yielding summetria, and originally indicated a relation of commensurability (such is the meaning codified in Euclid’s Elements for example).

What are symmetry considerations?

Symmetry considerations dominate modern fundamental physics, both in quantum theory and in relativity. Philosophers are now beginning to devote increasing attention to such issues as the significance of gauge symmetry, quantum particle identity in the light of permutation symmetry, how to make sense of parity violation, the role of symmetry breaking, the empirical status of symmetry principles, and so forth. These issues relate directly to traditional problems in the philosophy of science, including the status of the laws of nature, the relationships between mathematics, physical theory, and the world, and the extent to which mathematics suggests new physics.

What is unity of different and equal elements?

Summing up, a unity of different and equal elements is always associated with symmetry, in its ancient or modern sense; the way in which this unity is realized, on the one hand, and how the equal and different elements are chosen, on the other hand, determines the resulting symmetry and in what exactly it consists.

Who was the first to recognize the importance of symmetry groups in quantum physics?

Wigner and Weyl were among the first to recognize the great relevance of symmetry groups to quantum physics and the first to reflect on the meaning of this. As Wigner emphasized on many occasions, one essential reason for the “increased effectiveness of invariance principles in quantum theory” (Wigner, 1967, p.

Who discovered the SU symmetry?

This idea emerged by analogy with what happened in the case of permutation symmetry, and was in fact due to Heisenberg (the discoverer of permutation symmetry), who in a 1932 paper introduced the SU (2) symmetry connecting the proton and the neutron (interpreted as the two states of a single system).

Is Kepler's figure symmetric?

From a modern perspective, the regular figures used in Plato’s and Kepler’s physics for the mathematical proportions and harmonies they contain (and the related properties and beauty of their form) are symmetric in another sense that does not have to do with proportions.

What is symmetry breaking?

In physics, symmetry breaking is a phenomenon in which (infinitesimally) small fluctuations acting on a system crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations (or " noise "), the choice will appear arbitrary.

Why is symmetry breaking called symmetry breaking?

This process is called symmetry "breaking", because such transitions usually bring the system from a symmetric but disorderly state into one or more definite states. Symmetry breaking is thought to play a major role in pattern formation .

Who used the idea of symmetry breaking?

In his 1972 Science paper titled "More is different" Nobel laureate P.W. Anderson used the idea of symmetry breaking to show that even if reductionism is true, its converse, constructionism, which is the idea that scientists can easily predict complex phenomena given theories describing their components, is not.

Is symmetry breaking parametrized?

This is because the background ( spacetime) of the system, its vacuum, is non-invariant. Such a symmetry breaking is parametrized by an order parameter. A special case of this type of symmetry breaking is dynamical symmetry breaking .

Overview

As a kind of invariance

Local and global

Continuous

Discrete

Mathematics of physical symmetry

Mathematics

See also